1. 时间复杂度
1.1 分析思路
运行时间可以直观准确地反映一个算法的效率。
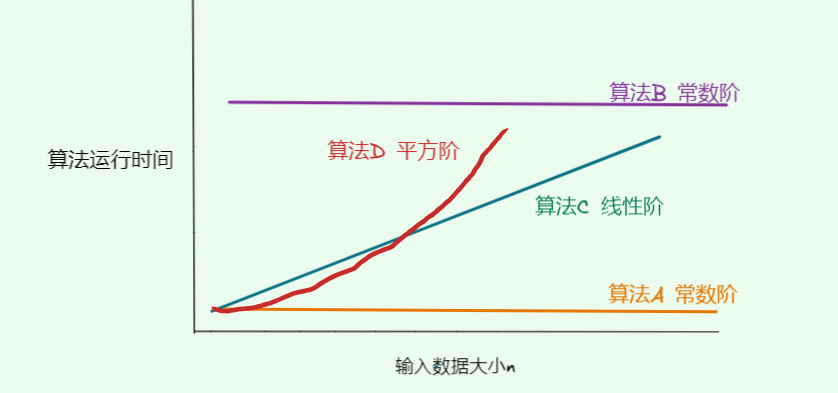
时间复杂度分析统计的不是算法运行的时间,运行时间和平台环境也有着很大的关系,这个不是我们能控制的,所以,我们统计算法运行时间随着数据量变大时的增长趋势,我们举个例子看一下,假设输入数据大小为 n n n
// 常数阶
void AlgorithmA(int n)
{
cout << "haha" << endl;
}
void AlgorithmB(int n)
{
for (size_t i = 0; i < 1024*1024; i++)
{
cout << "haha" << endl;
}
}
// 线性阶
void AlgorithmC(int n)
{
for (size_t i = 0; i < n; i++)
{
cout << "haha" << endl;
}
}
// 平方阶
void AlgorithmD(int n)
{
for (size_t i = 0; i < n; i++)
{
for (size_t j = 0; j < n; j++)
{
cout << "haha" << endl;
}
}
}
- A只有一个打印操作,运行时间不随
n
n
n增大而增大,B有
1024*1024次打印操作,虽然运行时间很长,但是运行时间也不随 n n n增大而增大,所以A和B算法都是常数阶 - B中打印操作要循环 n n n次,运行时间随着 n n n增大呈线性增长,属于线性阶
- C中打印操作要循环 n 2 n^2 n2次,运行时间随着 n n n增大呈平方趋势增长,属于平方阶
1.2 大O渐进表示法法
根据分析思路,我们估算算法的时间复杂度只需要估算量级即可
常见的量级有以下几种:
𝑂(1) < 𝑂(log 𝑛) < 𝑂(𝑛) < 𝑂(𝑛 log 𝑛) < 𝑂( 𝑛 2 𝑛^2 n2) < 𝑂( 2 𝑛 2^𝑛 2n) < 𝑂(𝑛!)
常数阶 < 对数阶 < 线性阶 < 线性对数阶 < 平方阶 < 指数阶 < 阶乘阶
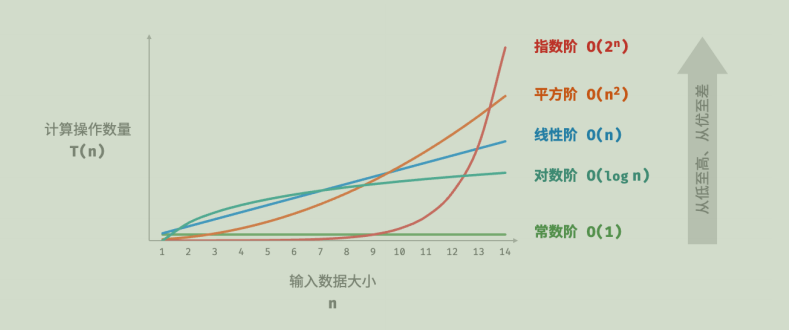
[声明]:此图来自hello‑algo.com
- 常数阶 O ( 1 ) O(1) O(1)
常数阶的操作数量与输入数据n的大小无关
// 常数阶
void AlgorithmB(int n)
{
for (size_t i = 0; i < 1024*1024; i++)
{
cout << "haha" << endl;
}
}
- 线性阶 O ( n ) O(n) O(n)
线性阶的操作数量与输入数据大小n呈线性级别增长,常出现在单层循环中
// 线性阶
void AlgorithmC(int n)
{
for (size_t i = 0; i < n; i++)
{
cout << "haha" << endl;
}
}
遍历数组,遍历链表等操作都是线性阶
// 线性阶
#include <vector>
int arrTraversal(vector<int>& nums)
{
int cnt = 0;
// 范围for
for (int e : nums)
{
cnt++;
}
return cnt;
}
- 平方阶 O ( n ) O(n) O(n)
平方阶的操作数量相对于输入数据大小 n n n呈平方级别增长。平方阶通常出现在嵌套循环中,内外层循环都为 O ( n ) O(n) O(n)
// 平方阶
void AlgorithmD(int n)
{
for (size_t i = 0; i < n; i++)
{
for (size_t j = 0; j < n; j++)
{
cout << "haha" << endl;
}
}
}
- 指数阶 O ( 2 n ) O(2^n) O(2n)
“细胞分离”就是指数增长的典型案例
斐波那契数列也是一个指数级增长的典型案例
// 指数阶
long long Fib(size_t n)
{
if(n < 3)
return 1;
return Fib(n-1) + Fib(n-2);
}
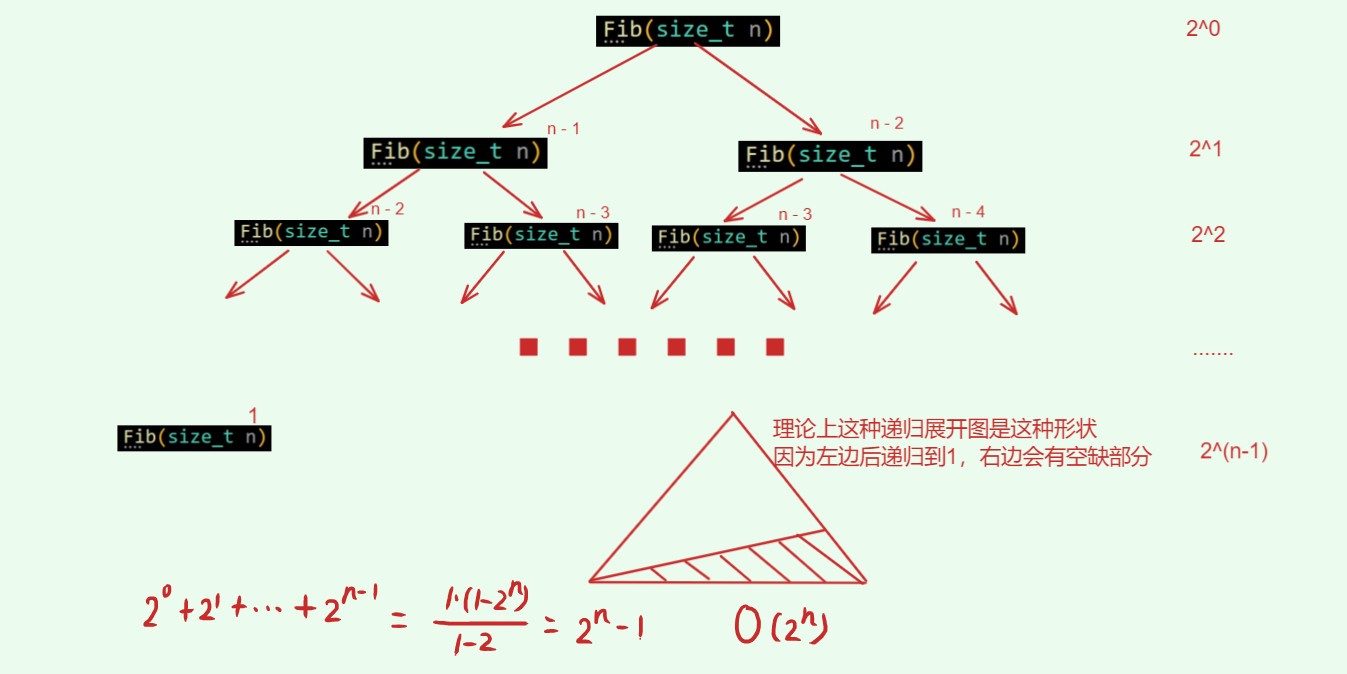
指数阶常常出现在递归中
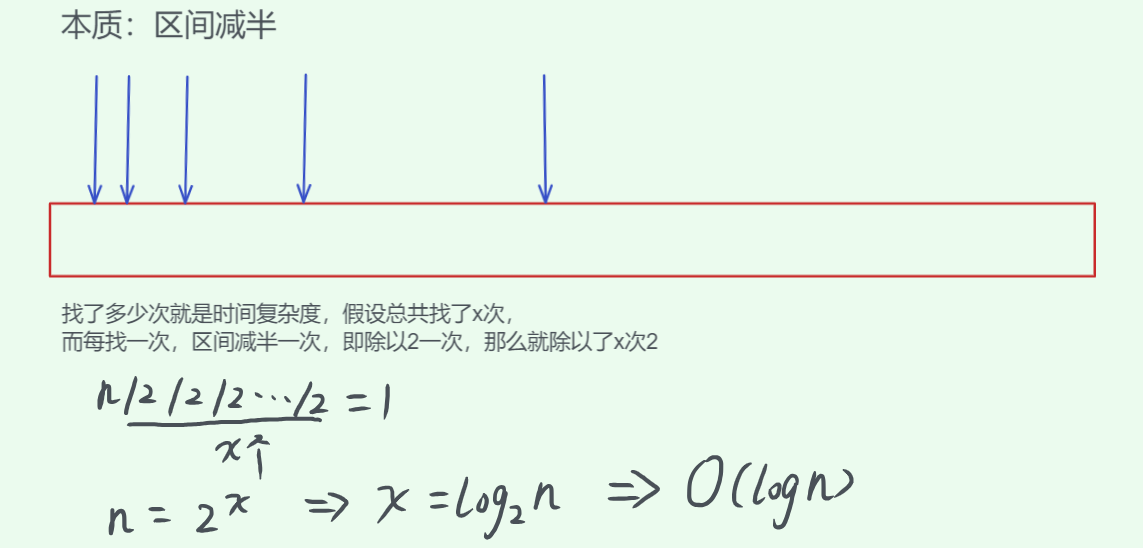
- 对数阶 O ( l o g n ) O(logn) O(logn)
和指数阶相反,对数阶反映“每轮缩减到一半”。设输入数据大小为 n n n,每轮缩减到原来的一般,循环次数是 log 2 n \log_2n log2n,为了书写方便,简记为 O ( l o g n ) O(logn) O(logn)
二分查找是一个典型的对数阶算法
// 对数阶
int BinarySearch(int* arr, int n, int x)
{
assert(arr);
int begin = 0;
int end = n - 1;
// [begin, end]:begin和end是左闭右闭区间,因此有=号
while (begin <= end)
{
int mid = begin + ((end - begin) >> 1);
if (arr[mid] < x)
begin = mid + 1;
else if (arr[mid] > x)
end = mid - 1;
else
return mid;
}
return -1;
}
还有个有趣的知识,假设中国十四亿人口,每个人的省份证号按序排列,找一个人最多需要找多少次?
可以利用二分查找的思想,我们知道
2 10 = 1024 , 2 20 = 1024 × 1024 , 2 30 = 1024 × 1024 × 1024 2^{10} = 1024,2^{20} = 1024\times1024, 2^{30} = 1024\times1024\times1024 210=1024,220=1024×1024,230=1024×1024×1024
而 2 30 的量级是 1 × 10 9 , 14 亿 = 1.4 × 10 9 ,所以我们最多需要找 31 次 而2^{30}的量级是1 \times 10^9,14亿 =1.4\times10^9,所以我们最多需要找31次 而230的量级是1×109,14亿=1.4×109,所以我们最多需要找31次
- 线性对数阶 O ( n l o g n ) O(nlogn) O(nlogn)
线性对数阶常出现在嵌套循环中,一层 O ( n ) O(n) O(n),一层 O ( l o g n ) O(logn) O(logn)
// 线性对数阶
int linerLogRecur(int n)
{
if (n <= 1)
return 1;
int cnt = linerLogRecur(n / 2) + linerLogRecur(n / 2);
for (size_t i = 0; i < n; i++)
{
cnt++;
}
return cnt;
}
- 阶乘阶== O ( n ! ) O(n!) O(n!)==
$n! = n \times (n - 1) \times (n - 2) \times … \times 2 \times 1 $
// 阶乘阶
int factorialRecur(int n)
{
if (n == 0)
return 1;
int cnt = 0;
// 从 1 个分裂出 n 个
for (size_t i = 0; i < n; i++)
{
cnt += factorialRecur(n - 1);
}
return cnt;
}
2. 空间复杂度
2.1 算法相关空间
- 输入空间: 存储算法的输入数据
- 暂存空间: 存储算法运行过程中的变量、对象、函数
- 输出空间: 存储算法的输出数据
一般情况,空间复杂度统计暂存空间和输出空间
暂存空间还可以分成三部分:
- 暂存数据: 保存算法运行中的常量、变量、对象
- 栈帧空间: 保存调用函数的上下文数据,每次调用函数都会在栈顶创建一个栈帧,函数返回后,栈帧空间会被释放
- 指令空间: 保存编译后的程序指令
2.2 分析方法
空间复杂度是临时占用存储空间大小的度量,函数运行时所要的栈帧空间在编译期间已经确定好了,因此空间复杂度主要通过函数在运行时显式额外申请的空来确定
然后请记住:空间可以复用,但是时间不行





















 2027
2027

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








