代码随想录算法训练营第 32 天 | 509. 斐波那契数、70. 爬楼梯、746. 使用最小花费爬楼梯

509. 斐波那契数

题目链接

1. 确定 dp[i] 含义。dp[i]：第 i 个斐波那契数值为 dp[i]
2. 递推公式。dp[i] = dp[i - 1] + dp[i - 2]
3. dp 数组如何初始化。dp[0] = 1, dp[1] = 1
4. 遍历顺序。从前向后
5. 打印 dp 数组

dp 数组：

class Solution {
    public int fib(int n) {
        // 0 <= n <= 30
        int[] dp = new int[31];
        dp[0] = 0;
        dp[1] = 1;
        for (int i = 2; i < 31; i++) {
            dp[i] = dp[i - 1] + dp[i - 2];
        }
        return dp[n];
    }
}

压缩：

class Solution {
    public int fib(int n) {
        // 0 <= n <= 30
        // 0, 1, 1, 2, 3
        // 0, 1, 2, 3, 4
        if (n < 2) {
            return n;
        }
        int p = 0;
        int q = 1;
        int sum = 0;
        for (int i = 2; i <= n; i++) {
            sum = p + q;
            p = q;
            q = sum;
        }
        return sum;
    }
}

---

70. 爬楼梯

题目链接

1. 确定 dp[i] 含义。dp[i]：达到 i 阶有 dp[i] 种方法
2. 递推公式。dp[i] = dp[i - 1] + dp[i - 2]
3. dp 数组如何初始化。dp[1] = 1, dp[2] = 2
4. 遍历顺序。从前向后
5. 打印 dp 数组

dp 数组：

class Solution {
    public int climbStairs(int n) {
        int[] dp = new int[n + 1];
        if (n == 1) {
            return n;
        }
        dp[1] = 1;
        dp[2] = 2;
        for (int i = 3; i < n + 1; i++) {
            dp[i] = dp[i - 1] + dp[i - 2];
        }
        return dp[n];
    }
}

压缩：

class Solution {
    public int climbStairs(int n) {
        int p = 0, q = 1, sum = 1;
        for (int i = 2; i <= n; i++) {
            p = q;
            q = sum;
            sum = p + q;
        }
        return sum;
    }
}

---

746. 使用最小花费爬楼梯

添加链接描述

1. 确定 dp[i] 含义。dp[i]：达到 i 位置最小花费为 dp[i]
2. 递推公式。dp[i] = Math.min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]
3. dp 数组如何初始化。dp[0] = 0, dp[1] = 0
4. 遍历顺序。从前向后
5. 打印 dp 数组

dp 数组：

class Solution {
    public int minCostClimbingStairs(int[] cost) {
        int n = cost.length;
        int[] dp = new int[n + 1];
        dp[0] = 0;
        dp[1] = 0;
        for (int i = 2; i <= n; i++) {
            dp[i] = Math.min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
        }
        return dp[n];
    }
}

压缩：

class Solution {
    public int minCostClimbingStairs(int[] cost) {
        int n = cost.length;
        int p = 0, q = 0, sum = 0;
        for (int i = 2; i <= n; i++) {
            sum = Math.min(q + cost[i - 1], p + cost[i - 2]);
            p = q;
            q = sum;
        }
        return sum;
    }
}

---

动态规划总结

动规五部曲：

1. dp 数组以及下标的含义
2. 递推公式
3. dp 数组如何初始化
4. 遍历顺序
5. 打印 dp 数组（出错时使用）

写代码的顺序与上相反：
先是确定 dp 数组及下标的含义，然后初始化数组，然后开始遍历，然后运用递推公式。

---

状态压缩的通用模板：

class Solution {
    public int xxx(int n) {
        int p = 0, q = 1, sum = 1;
        for (int i = k; i <= n; i++) { // k 为实际的第几个数。如 k = 2 表示计算第 2 个数的值
            p = q;
            q = sum;
            sum = p + q;
        }
        return sum;
    }
}

或

class Solution {
    public int xxx(int n) {
        int p = 0, q = 1, sum = 1;
        for (int i = k; i <= n; i++) { // k 为实际的第几个数。如 k = 2 表示计算第 2 个数的值
            sum = p + q;
            p = q;
            q = sum;
        }
        return sum;
    }
}

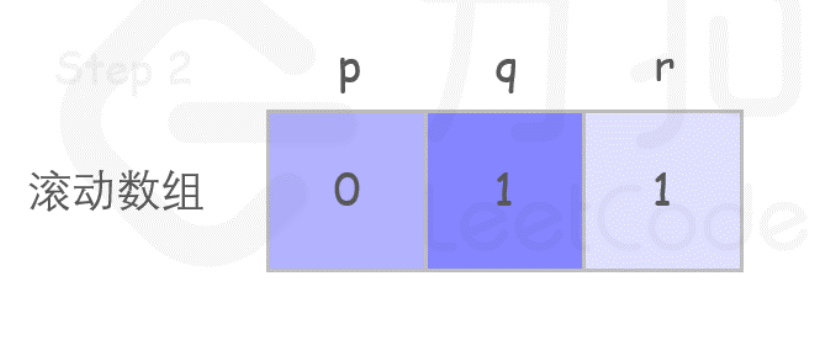
本质是滚动数组：

---