平凡前端之路_09.可变更的盒模型与多列布局支持

CSS 假定所有的HTML 文档元素都生成了一个描述该元素在HTML文档布局中所占空间的矩形元素框，可以形象地将其看作是一个盒子。

围绕这些盒子产生了一种“盒子模型”概念，定义了一系列与盒子相关的属性。

盒子的组成

盒子模型由四个部分：外边距/间距（margin）、边框（border）、内边距/填充（padding）、内容（content）组成。

通过对四部分属性的设置可以丰富盒子的表现效果。

---

标准盒子模型 - content-box

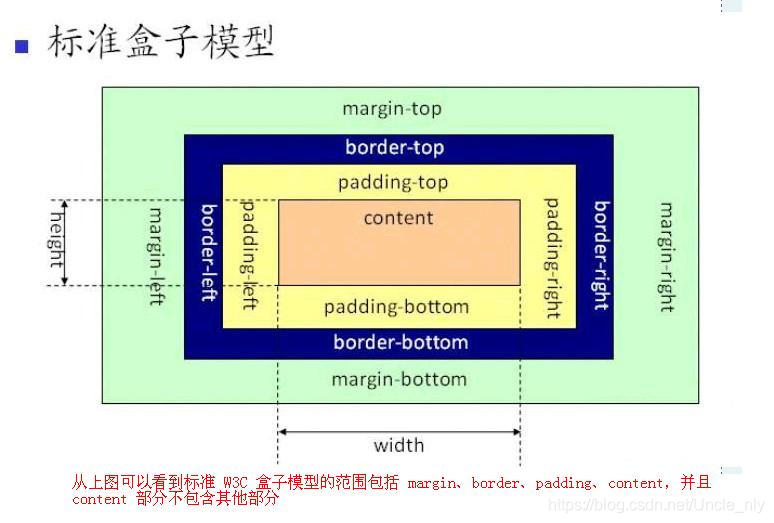
标准盒子的大小

标准盒子模型的范围包含margin、border、padding、content，并且content部分不包含其他部分，给标准盒子设置的width、height只是设置content区域的大小。

//标准盒子
.box {
    width: 200px;
    height: 180px;
    border: 5px solid #666;	//表示所有四个方向的边框共用相同的大小、样式、颜色。
    margin: 10px;			//表示所有四个方向的外边距共用相同的大小。
    padding: 10px;			//表示所有四个方向的内边距共用相同的大小。
}

//标准盒子占据的空间
  宽度	= 左外边距 + 左边框 + 左内边距 + 内容宽度 + 右内边距 + 右边框 + 右外边距
		= margin-left + border-left + padding-left + width + padding-right + border-right + margin-right
		= 10 + 5 + 10 + 200 + 10 + 5 + 10
		= 250
  高度 	= 上外边距 + 上边框 + 上内边距 + 内容高度 + 下内边距 + 下边框 + 下外边距
  		= margin-top + border-top + padding-top + height + padding-bottom + border-bottom + margin-bottom
  		= 10 + 5 + 10 + 180 + 10 + 5 + 10
    	= 230

//标准盒子的实际大小
  宽度	= 左边框 + 左内边距 + 内容宽度 + 右内边距 + 右边框
  		= border-left + padding-left + width + padding-right + border-right
  		= 5 + 10 + 200 + 10 + 5
  		= 230
  高度 	= 上边框 + 上内边距 + 内容高度 + 下内边距 + 下边框
  		= border-top + padding-top + height + padding-bottom + border-bottom
  		= 5 + 10 + 180 + 10 + 5
  		= 210

---

IE盒子模型 - border-box

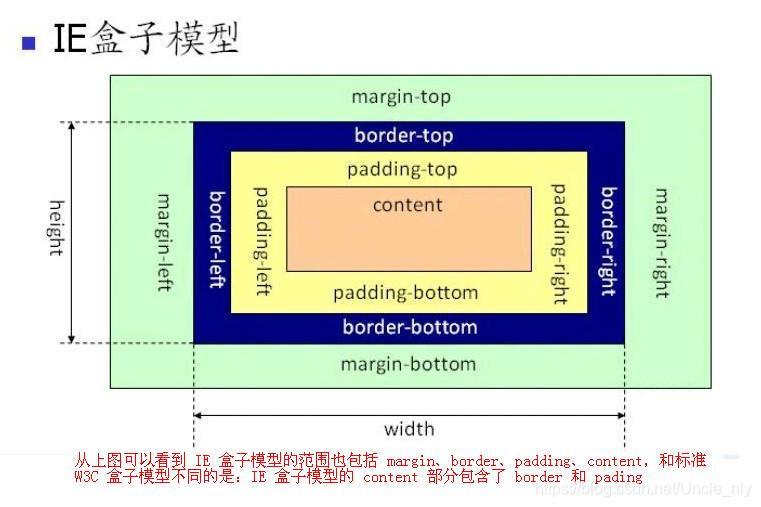
IE盒子的大小

IE盒子模型的范围包含margin、border、padding、content，盒子内容部分包含了content、border和padding，给IE盒子设置的width、height已经包含了content、border和padding区域。

//IE盒子
.box {
    width: 200px;
    height: 180px;
    border: 5px solid #666;	//表示所有四个方向的边框共用相同的大小、样式、颜色。
    margin: 10px;			//表示所有四个方向的外边距共用相同的大小。
    padding: 10px;			//表示所有四个方向的内边距共用相同的大小。
}

//IE盒子占据的空间
  宽度	= 左外边距 + 内容宽度 + 右外边距
		= [margin-left] + [width] + [margin-right]
		= 10 + 200 + 10
		= 220
  高度 	= 上外边距+ 内容高度 + 下外边距
  		= [margin-top] + [height] + [margin-bottom]
  		= 10 + 180 + 10
    	= 200

//IE盒子的实际大小
  宽度	= 内容宽度
  		= [width]
  		= 200 
  		= 200 
  高度 	= 内容高度
  		= [height]
  		= 180 
  		= 180 

---

指定盒子模型 - box-sizing

CSS3规范提供了box-sizing属性并允许设置浏览器使用content-box或者border-box盒模型。

box-sizing: content-box;

指定标准盒子，标准盒子设置的width、height只是设置content区域的大小，content部分不包含其他部分。

box-sizing: border-box;

指定IE盒子，给IE盒子设置的width、height已经包含了content、border和padding区域。

/* 兼容与支持 */
eg:
 	-webkit-box-sizing:  border-box; 	/* Safari 3.2 + */
 	   -moz-box-sizing:  border-box;	/* Firefox 2.0 + */
    		box-sizing:  border-box; 

box-sizing 的应用场景

当一个容器宽度定义为 width:100%; 之后，如果再增加 padding 或者 border 则会溢出父容器，是向外扩张的，可能导致变形。

如果指定为 box-sizing: border-box; 则 padding 和 border 就不会再溢出，而是向内收缩的，这个效果是非常实用的。

---

多列布局

CSS3 引入了多列布局将像报纸、杂志那样，把一个简单的区块拆分成多列。

---

多列中列数量 - column-count

column-count 属性指定了需要分割的列数。

column-count可能的值	描述
number	列的最佳数目将其中的元素的内容无法流出。
auto（默认）	列数将取决于其他属性，例如：column-width。

/*兼容与支持*/
eg:
	-webkit-column-count:3; /* Safari 3.1 + , Chrome 4.0 + and Opera 15.0 + */
	   -moz-column-count:3; /* Firefox 2.0 + */
			column-count:3;

---

多列中列宽度 - column-width

column-width属性指定列的宽度。

column-width可能的值	描述
length	指定列宽的长度。
auto（默认）	浏览器将决定列的宽度。

/*兼容与支持*/
eg:
	-webkit-column-width:300px; /* Safari 3.1 + , Chrome 4.0 + and Opera 15.0 + */
	   -moz-column-width:300px; /* Firefox 2.0 + */
			column-width:300px;

---

简写：多列数量和宽度 - columns

columns指定多列的列数量和列宽度。

columns是一个简写属性，可在声明中设置 column-width 和 column-count 属性。

columns: [column-count] [column-width] 
/*兼容与支持*/
eg:
	-webkit-columns:3 300px; /* Safari 3.1 + , Chrome 4.0 + and Opera 15.0 + */
	   -moz-columns:3 300px; /* Firefox 2.0 + */
			columns:3 300px;

---

多列之间的间隙 - column-gap

column-gap 属性指定了列与列间的间隙。

column-gap可能的值	描述
length	一个指定的长度，将设置列之间的差距。
normal（默认）	指定一个列之间的普通差距。

/*兼容与支持*/
eg:
	-webkit-column-gap:30px; /* Safari 3.1 + , Chrome 4.0 + and Opera 15.0 + */
	   -moz-column-gap:30px; /* Firefox 2.0 + */
			column-gap:30px;

---

多列中列之间的边框的宽度 - column-rule-width

column-rule-width属性指定列之间的边框的宽度。

column-rule-width 可能的值	描述
thin	指定细的边框。
medium（默认）	指定中等的边框。
thick	指定粗的边框。
length	允许指定边框的自定义宽度。

/*兼容与支持*/
eg:
	-webkit-column-rule-width:3px; /* Safari 3.1 + , Chrome 4.0 + and Opera 15.0 + */
	   -moz-column-rule-width:3px; /* Firefox 2.0 + */
			column-rule-width:3px;

---

多列中列之间的边框的样式 - column-rule-style

column-rule-style属性指定列之间的边框的样式。

column-rule-style可能的值	描述
dotted	指定点状边框。
dashed	指定虚线边框。
solid（默认）	指定实线边框。
double	指定双线边框。双线的宽度等于 column-rule-width 的值。
groove	指定凹槽边框。
ridge	指定垄状边框。
inset	指定inset边框。
outset	指定outse边框。

/*兼容与支持*/
eg:
	-webkit-column-rule-style:solid; /* Safari 3.1 + , Chrome 4.0 + and Opera 15.0 + */
	   -moz-column-rule-style:solid; /* Firefox 2.0 + */
			column-rule-style:solid;

---

多列中列之间的边框的颜色 - column-rule-color

column-rule-color属性指定列之间的边框的颜色。

column-rule-color可能的值	描述
color	指定边框的颜色。

/*兼容与支持*/
eg:
	-webkit-column-rule-color:#ff00ff; /* Safari 3.1 + , Chrome 4.0 + and Opera 15.0 + */
	   -moz-column-rule-color:#ff00ff; /* Firefox 2.0 + */
			column-rule-color:#ff00ff;

---

简写：多列中列之间的边框 - column-rule

column-rule指定列之间的边框：宽度，样式和颜色。

column-rule是一个简写属性，可在声明中设置 column-rule-width , column-rule-style 和 column-rule-color属性。

column-rule: [column-rule-width] [column-rule-style] [column-rule-color];
/*兼容与支持*/
eg:
	-webkit-column-rule:3px solid #ff00ff; /* Safari 3.1 + , Chrome 4.0 + and Opera 15.0 + */
	   -moz-column-rule:3px solid #ff00ff; /* Firefox 2.0 + */
			column-rule:3px solid #ff00ff;

---

多列中元素跨列 - column-span

column-span属性指定元素跨列。

column-span可能的值	描述
none	该元素不跨列。
all	该元素跨越所有列。

/*兼容与支持*/
eg:
	-webkit-column-span:all; /* Safari 3.1 + , Chrome 4.0 + and Opera 15.0 + */
			column-span:all;

---

CSS 知识题

题目	答案
让没有文本但有链接的a标签显示链接	a[href^=“http”]:empty::before { content: attr(href);}
行内元素是否具有盒子模型	行内元素同样具有盒子模型。
行内元素的padding、margin是否都有效	行内元素的padding-top、padding-bottom、margin-top、margin-bottom属性设置是无效的
相邻marign重叠的特性	margin 重叠必须发生在普通流元素中，只发生在垂直方向。
相邻marign重叠的三种情景	相邻兄弟元素的 margin 重叠；父子元素（第一个、最后一个）的 margin 重叠；元素自身的 margin-bottom 和 margin-top 折叠
参与marign重叠计算，一个外边距80，一个外边距50，计算最终 margin 值	参与marign重叠计算都是正值，最终 margin 值为 margin 较大的值为 （80）。
参与marign重叠计算，一个外边距-80，一个外边距50，计算最终 margin 值	参与marign重叠计算中有正值，有负值，最终 margin 值为正负值相加（-30）。
参与marign重叠计算，一个外边距-80，一个外边距-50，计算最终 margin 值	参与marign重叠计算都是负值，最终 margin 值取为 margin 较小的值为（-80）。