浪在ACM集训队寒假集训第二场

A. Generous Kefa

  One day Kefa found n baloons. For convenience, we denote color of i-th baloon as si — lowercase letter of the Latin alphabet. Also Kefa has k friends. Friend will be upset, If he get two baloons of the same color. Kefa want to give out all baloons to his friends. Help Kefa to find out, can he give out all his baloons, such that no one of his friens will be upset — print «YES», if he can, and «NO», otherwise. Note, that Kefa’s friend will not upset, if he doesn’t get baloons at all.

Input

  The first line contains two integers n and k (1 ≤ n, k ≤ 100) — the number of baloons and friends.
  Next line contains string s — colors of baloons.

Output

  Answer to the task — «YES» or «NO» in a single line.
  You can choose the case (lower or upper) for each letter arbitrary.

Examples

input
4 2
aabb
output
YES
input
6 3
aacaab
output
NO
Note
  In the first sample Kefa can give 1-st and 3-rd baloon to the first friend, and 2-nd and 4-th to the second.
  In the second sample Kefa needs to give to all his friends baloons of color a, but one baloon will stay, thats why answer is «NO».

解析

  这个题…就是分水桶,水桶有不同的颜色,他的鬼畜好友不能分到两个相同颜色的桶.当然,你可以不给不同好友不同数目的桶,只要保证每个人的颜色不同.所以…就解决了

#include<iostream>
#include<algorithm>
#include<string.h>
#include<queue>
#include<stdio.h>
#include<string>
#include<stdlib.h>
#include<map>
#ifndef NULL
#define NULL 0
#endif
using namespace std;

string s;
int a[27];
int main()
{
	int n,k,f=0;
	cin >> n >> k;
	cin >> s;
	for (int i = 0; i < n; i++)
		a[s[i] - 'a']++;
	for(int i=0;i<26;i++)
		if (a[i] != 0 &&a[i]>k) {
			cout << "NO" << endl;
			f = 1;
			break;
		}
	if (!f)
		cout << "YES" << endl;
	return 0;
}

B. Godsend

  Leha somehow found an array consisting of n integers. Looking at it, he came up with a task. Two players play the game on the array. Players move one by one. The first player can choose for his move a subsegment of non-zero length with an odd sum of numbers and remove it from the array, after that the remaining parts are glued together into one array and the game continues. The second player can choose a subsegment of non-zero length with an even sum and remove it. Loses the one who can not make a move. Who will win if both play optimally?

Input

  First line of input data contains single integer n (1 ≤ n ≤ 10⁶) — length of the array.
  Next line contains n integers a1, a2, …, an (0 ≤ ai ≤ 10⁹).

Output

  Output answer in single line. “First”, if first player wins, and “Second” otherwise (without quotes).

Examples

input
4
1 3 2 3
output
First
input
2
2 2
output
Second
Note
  In first sample first player remove whole array in one move and win.
  In second sample first player can’t make a move and lose.

解析

看着像博弈论,我倒觉得像是考数论.
就是第一个人可以在这一组里取出和为奇数的一串连续数字,第二个可以取出和为偶数且大于零的连续数字.谁能使对方不能拿,谁赢.
我也不太清楚怎么严格证明.我简单说一下我的思路.只要数字串内有一个奇数,那么甲必赢.

#include<iostream>
#include<algorithm>
#include<string.h>
#include<queue>
#include<stdio.h>
#include<string>
#include<stdlib.h>
#include<map>
#ifndef NULL
#define NULL 0
#endif
using namespace std;

int a[1000001], n;
int main()
{
	cin >> n;
	for (int i = 1; i <= n; i++) {
		cin >> a[i];
		if (a[i] % 2) {
			cout << "First" << endl;
			return 0;
		}
	}
	cout << "Second" << endl;
	return 0;
}

C. Leha and Function

  Leha like all kinds of strange things. Recently he liked the function F(n, k). Consider all possible k-element subsets of the set [1, 2, …, n]. For subset find minimal element in it. F(n, k) — mathematical expectation of the minimal element among all k-element subsets.
  But only function does not interest him. He wants to do interesting things with it. Mom brought him two arrays A and B, each consists of m integers. For all i, j such that 1 ≤ i, j ≤ m the condition Ai ≥ Bj holds. Help Leha rearrange the numbers in the array A so that the sum is maximally possible, where A’ is already rearranged array.

Input

  First line of input data contains single integer m (1 ≤ m ≤ 2·10⁵) — length of arrays A and B.
  Next line contains m integers a1, a2, …, am (1 ≤ ai ≤ 10⁹) — array A.
  Next line contains m integers b1, b2, …, bm (1 ≤ bi ≤ 10⁹) — array B.

Output

  Output m integers a’1, a’2, …, a’m — array A’ which is permutation of the array A.

Examples

input
5
7 3 5 3 4
2 1 3 2 3
output
4 7 3 5 3
input
7
4 6 5 8 8 2 6
2 1 2 2 1 1 2
output
2 6 4 5 8 8 6

解析

  比赛的时候硬是没搞懂这鬼题什么意思.结束了好好研究了一下,贪心,别跟我说什么数论,什么数学期望.
  大意是说:f(n,k)指的是从n里面拿出k个数.从k个数里面找到最小的数的数学期望是多少.列如k=1的话a,就是a.两个数a,b就是(a+b)/2,数学期望都会,就不多嘴了.要求排列a,和b相加,使得无论k取多少,都是所有排列里期望最大的.
  解法,就贪心呗,让最大的数和最小的数对应,就完事了.
  我的解法和样例有不同,但是只要相同的数对应对了就行.

#include<iostream>
#include<algorithm>
#include<string.h>
#include<queue>
#include<stdio.h>
#include<string>
#include<math.h>
#include<stdlib.h>
#ifndef NULL
#define NULL 0
#endif
using namespace std;

typedef long long ll;
struct vec {
	ll x, id;
}a[2 * 100000 + 17],b[2 * 100000 + 17];
bool cmp(vec c, vec d)
{
	return c.x < d.x;
}
bool cmp1(vec c, vec d)
{
	return c.id < d.id;
}
int main()
{
	int n;
	cin >> n;
	for (int i = 0; i < n; i++) {
		cin >> a[i].x;
		a[i].id = i;
	}
	for (int i = 0; i < n; i++) {
		cin >> b[i].x;
		b[i].id = i;
	}
	sort(a, a + n, cmp);
	sort(b, b + n, cmp);
	for (int i = 0; i < n; i++)
		b[i].x = a[n - i - 1].x;
	sort(b, b + n, cmp1);
	for (int i = 0; i < n; i++)
		cout << b[i].x<<' ';
	return 0;
}

D. Leha and another game about graph

  Leha plays a computer game, where is on each level is given a connected graph with n vertices and m edges. Graph can contain multiple edges, but can not contain self loops. Each vertex has an integer di, which can be equal to 0, 1 or  - 1. To pass the level, he needs to find a «good» subset of edges of the graph or say, that it doesn’t exist. Subset is called «good», if by by leaving only edges from this subset in the original graph, we obtain the following: for every vertex i, di =  - 1 or it’s degree modulo 2 is equal to di. Leha wants to pass the game as soon as possible and ask you to help him. In case of multiple correct answers, print any of them.

Input

  The first line contains two integers n, m (1 ≤ n ≤ 3·105, n - 1 ≤ m ≤ 3·105) — number of vertices and edges.
  The second line contains n integers d1, d2, …, dn ( - 1 ≤ di ≤ 1) — numbers on the vertices.
  Each of the next m lines contains two integers u and v (1 ≤ u, v ≤ n) — edges. It’s guaranteed, that graph in the input is connected.

Output

  Print  - 1 in a single line, if solution doesn’t exist. Otherwise in the first line k — number of edges in a subset. In the next k lines indexes of edges. Edges are numerated in order as they are given in the input, starting from 1.

Examples

input
1 0
1
output
-1
input
4 5
0 0 0 -1
1 2
2 3
3 4
1 4
2 4
output
0
input
2 1
1 1
1 2
output
1
1
input
3 3
0 -1 1
1 2
2 3
1 3
output
1
2
Note
  In the first sample we have single vertex without edges. It’s degree is 0 and we can not get 1.

E. New Year and Ancient Prophecy

  Limak is a little polar bear. In the snow he found a scroll with the ancient prophecy. Limak doesn’t know any ancient languages and thus is unable to understand the prophecy. But he knows digits!
  One fragment of the prophecy is a sequence of n digits. The first digit isn’t zero. Limak thinks that it’s a list of some special years. It’s hard to see any commas or spaces, so maybe ancient people didn’t use them. Now Limak wonders what years are listed there.
  Limak assumes three things:
  Years are listed in the strictly increasing order;
  Every year is a positive integer number;
  There are no leading zeros.
  Limak is going to consider all possible ways to split a sequence into numbers (years), satisfying the conditions above. He will do it without any help. However, he asked you to tell him the number of ways to do so. Since this number may be very large, you are only asked to calculate it modulo 10⁹+ 7.

Input

  The first line of the input contains a single integer n (1 ≤ n ≤ 5000) — the number of digits.
  The second line contains a string of digits and has length equal to n. It’s guaranteed that the first digit is not ‘0’.

Output

  Print the number of ways to correctly split the given sequence modulo 10⁹ + 7.

Examples

input
6
123434
output
8
input
8
20152016
output
4
Note
  In the first sample there are 8 ways to split the sequence:
  “123434” = “123434” (maybe the given sequence is just one big number)
  “123434” = “1” + “23434”
  “123434” = “12” + “3434”
  “123434” = “123” + “434”
  “123434” = “1” + “23” + “434”
  “123434” = “1” + “2” + “3434”
  “123434” = “1” + “2” + “3” + “434”
  “123434” = “1” + “2” + “3” + “4” + “34”
  Note that we don’t count a split “123434” = “12” + “34” + “34” because numbers have to be strictly increasing.
  In the second sample there are 4 ways:
  “20152016” = “20152016”
  “20152016” = “20” + “152016”
  “20152016” = “201” + “52016”
  “20152016” = “2015” + “2016”

F. New Year and Days

  Today is Wednesday, the third day of the week. What’s more interesting is that tomorrow is the last day of the year 2015.
  Limak is a little polar bear. He enjoyed this year a lot. Now, he is so eager to the coming year 2016.
  Limak wants to prove how responsible a bear he is. He is going to regularly save candies for the entire year 2016! He considers various saving plans. He can save one candy either on some fixed day of the week or on some fixed day of the month.
  Limak chose one particular plan. He isn’t sure how many candies he will save in the 2016 with his plan. Please, calculate it and tell him.

Input

  The only line of the input is in one of the following two formats:
  “x of week” where x (1 ≤ x ≤ 7) denotes the day of the week. The 1-st day is Monday and the 7-th one is Sunday.
  “x of month” where x (1 ≤ x ≤ 31) denotes the day of the month.

Output

  Print one integer — the number of candies Limak will save in the year 2016.

Examples

input
4 of week
output
52
input
30 of month
output
11
Note
  Polar bears use the Gregorian calendar. It is the most common calendar and you likely use it too. You can read about it on Wikipedia if you want to – https://en.wikipedia.org/wiki/Gregorian_calendar. The week starts with Monday.
  In the first sample Limak wants to save one candy on each Thursday (the 4-th day of the week). There are 52 Thursdays in the 2016. Thus, he will save 52 candies in total.
  In the second sample Limak wants to save one candy on the 30-th day of each month. There is the 30-th day in exactly 11 months in the 2016 — all months but February. It means that Limak will save 11 candies in total.

解析

这个…拿出日历数一下就是了

#include<iostream>
#include<algorithm>
#include<string.h>
#include<queue>
#include<stdio.h>
#include<string>
#include<stdlib.h>
#include<map>
#ifndef NULL
#define NULL 0
#endif
using namespace std;

string s,a;
int main()
{
	int n;
	cin >> n >> a >> s;
	if (s == "month") {
		if (n <= 29)
			cout << 12 << endl;
		else if (n <= 30)
			cout << 11 << endl;
		else if (n <= 31)
			cout << 7 << endl;
		else
			cout << 0 << endl;
	}
	else if (s == "week") {
		if ((n >= 1 && n <= 4) || n == 7)
			cout << 52 << endl;
		else if (n == 5 || n == 6)
			cout << 53 << endl;
	}
	return 0;
}

G. New Year and Domino

  They say “years are like dominoes, tumbling one after the other”. But would a year fit into a grid? I don’t think so.
  Limak is a little polar bear who loves to play. He has recently got a rectangular grid with h rows and w columns. Each cell is a square, either empty (denoted by ‘.’) or forbidden (denoted by ‘#’). Rows are numbered 1 through h from top to bottom. Columns are numbered 1 through w from left to right.
  Also, Limak has a single domino. He wants to put it somewhere in a grid. A domino will occupy exactly two adjacent cells, located either in one row or in one column. Both adjacent cells must be empty and must be inside a grid.
  Limak needs more fun and thus he is going to consider some queries. In each query he chooses some rectangle and wonders, how many way are there to put a single domino inside of the chosen rectangle?

Input

  The first line of the input contains two integers h and w (1 ≤ h, w ≤ 500) – the number of rows and the number of columns, respectively.
  The next h lines describe a grid. Each line contains a string of the length w. Each character is either ‘.’ or ‘#’ — denoting an empty or forbidden cell, respectively.
  The next line contains a single integer q (1 ≤ q ≤ 100 000) — the number of queries.
  Each of the next q lines contains four integers r1i, c1i, r2i, c2i (1 ≤ r1i ≤ r2i ≤ h, 1 ≤ c1i ≤ c2i ≤ w) — the i-th query. Numbers r1i and c1i denote the row and the column (respectively) of the upper left cell of the rectangle. Numbers r2i and c2i denote the row and the column (respectively) of the bottom right cell of the rectangle.

Output

  Print q integers, i-th should be equal to the number of ways to put a single domino inside the i-th rectangle.

Examples

input
5 8
…#…#
.#…
##.#…
##…#.##
…
4
1 1 2 3
4 1 4 1
1 2 4 5
2 5 5 8
output
4
0
10
15
input
7 39
…
.###…###…#…###…###…###…#…###.
…#…#.#…#…#…#…#.#…#…#…
.###…#.#…#…###…###…#.#…#…###.
.#…#.#…#…#…#…#.#…#…#.#.
.###…###…#…###…###…###…#…###.
…
6
1 1 3 20
2 10 6 30
2 10 7 30
2 2 7 7
1 7 7 7
1 8 7 8
output
53
89
120
23
0
2
Note
  A red frame below corresponds to the first query of the first sample. A domino can be placed in 4 possible ways.

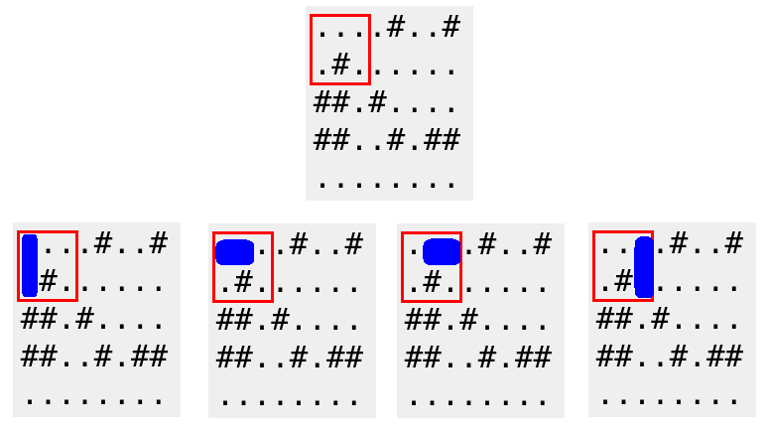
解析

  看图就能懂的题目.
  可以知道,只能横着或者竖着放木牌.那么我们就可以考虑二维前缀和的思想.
  首先,前缀和,指的是dp[i]={for j=0 to i aj}的和.二维前缀和,指的是矩阵,从(0,0)到(n,m)的和.
  之后,我们这个题,只需要求出每一行的前缀和,和每一列的前缀和.然后计算一下就可以了.

#include<iostream>
#include<algorithm>
#include<string>
#include<string.h>
#include<queue>
#include<stdio.h>
#include<stdlib.h>
#include<map>
#ifndef NULL
#define NULL 0
#endif
#define MAX 5001
using namespace std;

int d[MAX][MAX], r[MAX][MAX], dd[MAX], rr[MAX];
char mp[MAX][MAX];
int main()
{
	int n, m;
	cin >> n >> m;
	for (int i = 1; i <= n; i++){
		cin >> mp[i]+1;
		for(int j=1;j<=m;j++)
			if (mp[i][j] == '.'&&mp[i][j - 1] == '.')
				d[i][j] = 1 + d[i][j - 1];
			else
				d[i][j] = d[i][j - 1];
	}
	for (int j = 1; j <= m; j++)
		for (int i = 1; i <= n; i++)
			if (mp[i][j] == '.'&&mp[i - 1][j] == '.')
				r[i][j] = 1 + r[i - 1][j];
			else
				r[i][j] = r[i - 1][j];
	int q;
	cin >> q;
	for (int i = 0; i < q; i++) {
		long long res = 0;
		int c1, c2, r1, r2;
		cin >> r1 >> c1 >> r2 >> c2;
		for (int j = r1; j <= r2; j++)
			res += (d[j][c2] - d[j][c1]);
		for (int j = c1; j <= c2; j++)
			res += (r[r2][j] - r[r1][j]);
		cout << res << endl;
	}
	return 0;
}

H.New Year and Old Property

  The year 2015 is almost over.
  Limak is a little polar bear. He has recently learnt about the binary system. He noticed that the passing year has exactly one zero in its representation in the binary system — 2015 = 11111011111. Note that he doesn’t care about the number of zeros in the decimal representation.
  Limak chose some interval of years. He is going to count all years from this interval that have exactly one zero in the binary representation. Can you do it faster?
  Assume that all positive integers are always written without leading zeros.

Input

  The only line of the input contains two integers a and b (1 ≤ a ≤ b ≤ 10¹⁸) — the first year and the last year in Limak’s interval respectively.

Output

  Print one integer – the number of years Limak will count in his chosen interval.

Examples

input
5 10
output
2
input
2015 2015
output
1
input
100 105
output
0
input
72057594000000000 72057595000000000
output
26
Note
  In the first sample Limak’s interval contains numbers 5 = 101, 6 = 110, 7 = 111, 8= 1000, 9 = 1001 and 10 = 1010. Two of them (101and 110) have the described property.

解析

嗯,水题,暴力枚举结束,用一个小剪枝可以降低巨大的复杂度.
首先,a和b可以用long long存下来,这是重点.这个题问我们,在a和b之间,有多少个数的二进制表达,只有一个0.
那么我们可以把10¹⁸里的所有数的二进制都表达出来,然后看哪些只有一个0,妥妥超时.
那我们从a~b之间所有数的二进制表达出来,再一个个查,妥妥超时.
那我们把所有二进制只有一个0的数枚举出来,在[a,b]内的存下来.恭喜你,卡极限AC.
如果不想耗时这么难看,我们可以把a的二进制数共有len1位,b的二进制数len2位,存下来.然后在[len1,len2]长度内进行枚举’0’的位置.并判断是否在[a,b]内.其次,我们还可以知道,二进制的首位不为0,所以又可以少一次循环.
于是ac代码如下.当然,想手搓快速幂我也不拦你

#include<iostream>
#include<algorithm>
#include<string.h>
#include<queue>
#include<stdio.h>
#include<string>
#include<math.h>
#include<stdlib.h>
#ifndef NULL
#define NULL 0
#endif
using namespace std;

typedef long long ll;
int main()
{
	ll a, b,ans=0,len1=0,len2=0;
	cin >> a >> b;
	for (ll i = a; i > 0; i >>= 1)
		len1++;
	for (ll i = b; i > 0; i >>= 1)
		len2++;
	for (ll i = len1; i <= len2; i++)
		for (ll j = 0; j < i-1; j++) {
			ll c = 0;
			for (ll k = 0; k < i; k++)
				if (k != j)
					c += (ll)pow(2, k);
			if (c >= a && c <= b)
				ans++;
		}
	cout << ans << endl;
	return 0;
}