电力网络最大流算法-优快云博客

Power Network

Time Limit: 2000MS		Memory Limit: 32768K
Total Submissions: 24182		Accepted: 12609

Description

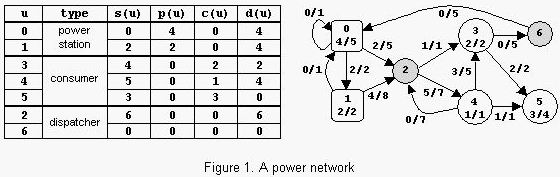
A power network consists of nodes (power stations, consumers and dispatchers) connected by power transport lines. A node u may be supplied with an amount s(u) >= 0 of power, may produce an amount 0 <= p(u) <= p _max(u) of power, may consume an amount 0 <= c(u) <= min(s(u),c _max(u)) of power, and may deliver an amount d(u)=s(u)+p(u)-c(u) of power. The following restrictions apply: c(u)=0 for any power station, p(u)=0 for any consumer, and p(u)=c(u)=0 for any dispatcher. There is at most one power transport line (u,v) from a node u to a node v in the net; it transports an amount 0 <= l(u,v) <= l _max(u,v) of power delivered by u to v. Let Con=Σ _uc(u) be the power consumed in the net. The problem is to compute the maximum value of Con.

An example is in figure 1. The label x/y of power station u shows that p(u)=x and p _max(u)=y. The label x/y of consumer u shows that c(u)=x and c _max(u)=y. The label x/y of power transport line (u,v) shows that l(u,v)=x and l _max(u,v)=y. The power consumed is Con=6. Notice that there are other possible states of the network but the value of Con cannot exceed 6.

Input

There are several data sets in the input. Each data set encodes a power network. It starts with four integers: 0 <= n <= 100 (nodes), 0 <= np <= n (power stations), 0 <= nc <= n (consumers), and 0 <= m <= n^2 (power transport lines). Follow m data triplets (u,v)z, where u and v are node identifiers (starting from 0) and 0 <= z <= 1000 is the value of l _max(u,v). Follow np doublets (u)z, where u is the identifier of a power station and 0 <= z <= 10000 is the value of p _max(u). The data set ends with nc doublets (u)z, where u is the identifier of a consumer and 0 <= z <= 10000 is the value of c _max(u). All input numbers are integers. Except the (u,v)z triplets and the (u)z doublets, which do not contain white spaces, white spaces can occur freely in input. Input data terminate with an end of file and are correct.

Output

For each data set from the input, the program prints on the standard output the maximum amount of power that can be consumed in the corresponding network. Each result has an integral value and is printed from the beginning of a separate line.

Sample Input

2 1 1 2 (0,1)20 (1,0)10 (0)15 (1)20
7 2 3 13 (0,0)1 (0,1)2 (0,2)5 (1,0)1 (1,2)8 (2,3)1 (2,4)7
         (3,5)2 (3,6)5 (4,2)7 (4,3)5 (4,5)1 (6,0)5
         (0)5 (1)2 (3)2 (4)1 (5)4

Sample Output

15
6

Hint

The sample input contains two data sets. The first data set encodes a network with 2 nodes, power station 0 with pmax(0)=15 and consumer 1 with cmax(1)=20, and 2 power transport lines with lmax(0,1)=20 and lmax(1,0)=10. The maximum value of Con is 15. The second data set encodes the network from figure 1.

Source

Southeastern Europe 2003

题目大意：输入n，np，nc，m，其中n是总结点数，np是power station的数量，nc是customer的数量，m代表m条有向边，然后的np组数据，代表power station的编号和最大允许通过的流量。接下来的nc组数据，代表customer的编号和通过这个节点会消耗掉的流量，要求求出整个图中会消耗掉的流量的最大值。

思路：根据节点的特点，power station有一个允许通过的最大流量w。因此设源点n向每个power station节点连一条w的边。customer节点会消耗掉一部分流量c，设立汇点n+1，

每一个customer节点向汇点连一条容量为c的边。最大流的结果就是流在这个网络中流通的最大消耗量。

这一题Ford_Fullerson算法超时，Dinic算法可以过。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<vector>
#include<queue>
using namespace std;
#define MAXN 110
#define Min(a,b)(a<b?a:b)
#define INF 0x0fffffff

int n,np,nc,m;

struct edge
{
int to,cap,rev;
edge(){}
edge(int a,int b,int c):to(a),cap(b),rev(c){}
};
vector<edge>G[MAXN];
int level[MAXN];
int iter[MAXN];

void bfs(int s)
{
memset(level,-1,sizeof(level));
queue<int>que;
que.push(s);
level[s]=0;
while(!que.empty())
{
  int v=que.front();
  que.pop();
  int i;
  for(i=0;i<G[v].size();i++)
  {
   edge &e=G[v][i];
   if(e.cap>0&&level[e.to]<0)
   {
    level[e.to]=level[v]+1;
    que.push(e.to);
   }
  }
}
}

int dfs(int v,int t,int f)
{
if(v==t)
  return f;
for(int i=0;i<G[v].size();i++)
{
  edge &e=G[v][i];
   if(e.cap>0&&level[v]<level[e.to])
   {
    int d=dfs(e.to,t,Min(f,e.cap));
    if(d>0)
    {
     e.cap-=d;
     G[e.to][e.rev].cap+=d;
     return d;
    }
   }
}
return 0;
}

int max_flow(int s,int t)
{
int flow=0;
while(1)
{
  bfs(s);
  if(level[t]<0)
   return flow;
  memset(iter,0,sizeof(iter));
  int f;
  while((f=dfs(s,t,INF))>0)
   flow+=f;
}
}
void addEdge(int u,int v,int w)
{
G[u].push_back(edge(v,w,G[v].size()));
G[v].push_back(edge(u,0,G[u].size()-1));
}

int main()
{
// freopen("C:\\1.txt","r",stdin);
while(~scanf("%d%d%d%d",&n,&np,&nc,&m))
{
  int st=n;
  int ed=n+1;
     char s[30];
        int i;
        for(i=0;i<MAXN;i++)
          G[i].clear();
        for(i=0;i<m;i++)
        {
        int u,v,w;
   scanf("%s",s);
        sscanf(s,"(%d,%d)%d",&u,&v,&w);
        addEdge(u,v,w);
        }
          for(i=0;i<np;i++)
          {
          int v,w;
   scanf("%s",s);
        sscanf(s,"(%d)%d",&v,&w);
          addEdge(st,v,w);
          }
          for(i=0;i<nc;i++)
          {
          int u,w;
   scanf("%s",s);
        sscanf(s,"(%d)%d",&u,&w);
          addEdge(u,ed,w);
          }
//   for(i=0;i<=n+1;i++)
//    for(int j=0;j<G[i].size();j++)
//     printf("(%d,%d)%d\n",i,G[i][j].to,G[i][j].cap);
          printf("%d\n",max_flow(st,ed));
}
return 0;
}