10343 划分凸多边形（优先做）

题目描述

10343 划分凸多边形（优先做）
时间限制:800MS 代码长度限制:10KB
提交次数:0 通过次数:0

题型: 编程题 语言: G++;GCC;VC;JAVA
Description
问题描述：一个正凸N边形，可以用N-3条互不相交的对角线将正N边形分成N-2个三角形。
现在要求读入N边形的N（N≤20），输出不同划分方法的总数（要求解的是划分方法数，而不需要输出各种划分法）。

这里，注意：
（1）顶点编号，认为顶点皆不相同，因此不允许认为将凸N边形转置视为相同划分。
（2）若输出是“No answer”，请注意大小写和无标点。

输入输出举例：
输入: N＝3， 输出：1
输入: N＝5， 输出：5
输入: N＝2， 输出：No answer
输入: N＝6， 输出：14
输入: N＝8， 输出：132

例如：
当N＝5时，共有5种分法。

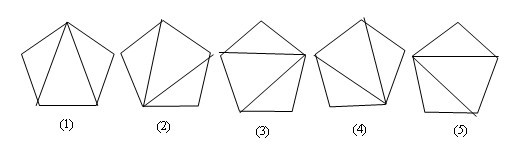
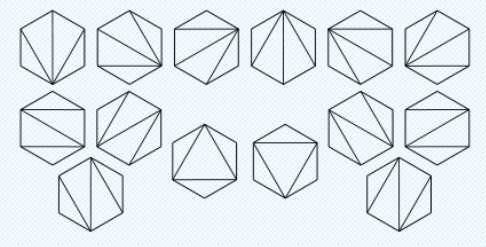
当N＝6时，对六边形的三角形所有划分，请看下图:

输入格式
N，代表正凸N边形。

输出格式
不同划分方法的总数。

输入样例
5

输出样例
5

提示

题目所求的是分法总数，并不要求具体的分法。而且，N可以大到21。
因此，用简单搜索或枚举会耗时较多，而应该想方设法找出N为不同值时，分法总数的变化规律。

把一个正凸N边形的各个顶点按照顺时针分别编上1，2，……，N。
顶点1，顶点N和顶点I（I∈[2, N-1]）能够构成一个三角形S。
这样凸N边形就被分成三部分：一个三角形S、一个I边形和一个N+1-I边形（I, N+1-I∈[2, N-1]）。
因此，凸N边形分为三角形总数Total(N)等于I边形的分法总数乘以N+1-I边形的分法总数之积，还要
在I分别取2，3，……，N－1时都累加起来。

递推公式如下：
Total(N) = sum{ Total(I)*Total(N+1-I) | for I=2 to N-1} if N>=4
Total(2) = Total(3) = 1

注意： 2点的多边形视为蜕化的多边形，定义其Total(2)=1，是为递推公式推导用。
但按题目意思当N=2时输出无解。

另外，此题需要注意的是，如果你写的纯递归程序可能会超时的，因为这里递归存在重复，且重复数量庞大。
需要用数组将你算过的元素存储下来，避免重复的递归计算，这样优化后，才能通过。

代码

#include <iostream>
#define N 30

int p[N];

using namespace std;

void coutQ(int n){
    for(int i=0;i<n;i++)p[i]=0;
    p[2]=1,p[3]=1;
    //双重循环 记录数据q[i]
    for(int i=4;i<=n;i++){
        for(int k=2;k<n;k++){
            p[i]+=p[k]*p[i-k+1];
        }
    }
}


int main(){
    int n;
    scanf("%d",&n);
    coutQ(n);
    if(n==1||n==2)printf("No answer");
    else printf("%d",p[n]);
    return 0;
}