【算法设计与分析】-- 回溯法

最新推荐文章于 2025-05-15 11:29:09 发布

四月天行健

最新推荐文章于 2025-05-15 11:29:09 发布

阅读量4.6k

点赞数 6

CC 4.0 BY-SA版权

分类专栏：算法设计与分析文章标签：算法数据结构 c++

本文链接：https://blog.youkuaiyun.com/Tir_zhang/article/details/127229024

算法设计与分析专栏收录该内容

5 篇文章

订阅专栏

本文详细介绍了回溯法的基本思想及应用，包括N皇后问题和图的M着色问题的具体解决方法。通过实例讲解了如何构造解空间树，并采用深度优先搜索策略来解决问题。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

一、基本思想

        回溯法有“通用的解题法”之称。用它可以求出问题的所有解(全部可行解或一个最优解)或任一解(可行解一解空间中满足约束条件的解)。

        回溯法是一个既带有系统性又带有跳跃性的搜索法。它在包含问题所有解的解空间树中，按照深度优先的策略，从根出发进行搜索。搜索每到达解空间树的一个结点，总是先判断以该结点为根的子树(或结点)是否肯定不包含问题的解。如果肯定不包含，则跳过对该子树的系统搜索，一层一层地向它的祖先回溯，直到遇上一个还有未被搜索过的儿子的结点，才转向该结点的一个未曾搜索过的儿子结点，继续搜索;否则，进入该子树，继续按深优先的策略进行搜索。

        回溯法在用来求问题的所有解(或最优解)时，要回溯到根，且根的所有儿子都已被搜索过才结束;而在用来求问题的任一解时，只要搜索到问题的一个解就可结束。

问题的解空间

例：对于有n种可选物品的0-1背包问题，其解空间由长度为n的0-1向量组成。该解空间包含了对变量的所有可能的0-1赋值，当n=3时，其解空间是：

{（0，0，0），（0，1，0），（0，0，1），（1，0，0），（0，1，1），（1，0，1），（1，1，0），（1，1，1）}

问题的解空间树

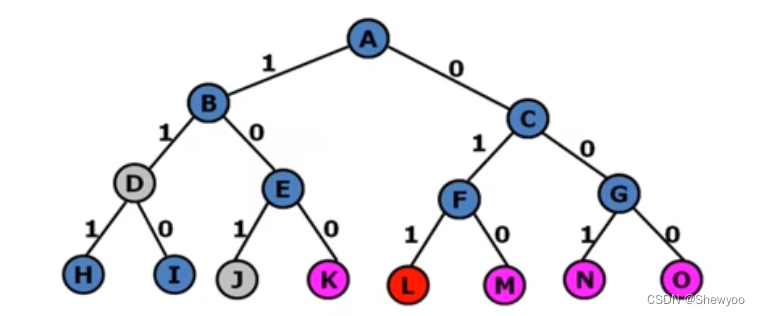
例:对于n=3时的0-1背包问题，其解空间用一棵完全二叉树表示：

搜索解空间树（回溯法的基本思想）

确定了解空间的组织结构后，回溯法就从开始结点(根结点)出发，以深度优先的方式搜索整个解空间。这个开始结点就成为一个活结点，同时也成为当前的扩展结点。在当前的扩展结点处，搜索向纵深方向移至一-个新结点。这个新结点就成为一个新的活结点，并成为当前的扩展结点。如果当前的扩展结点处不能再向纵深方向移动，则当前的扩展结点就成为死结点。此时应回溯到最近的一个活结点处，并使这个活结点成为当前的扩展结点。回溯法即以这种工作方式递归地在解空间中搜索，直至找到所要求的解或解空间中已无活结点时为止。

例：物品个数n = 3的0-1背包问题。W = [16,15,15]，V = [45,25,25]，c = 30.

对本例来说，图中的结点K、L、M、N、O分别对应一个可行解。如K结点100，只放入第一个物品可行，L结点011：放入第二三个物品也可行。结点K相应的解的价值是45，L是50，M25，N25，O0，结点L对应一个最优解。

子集树与排列树

当所给的问题是从n个元素的集合S中找出满足某种性质的子集时，相应的解空间树称为子集树。

void Backtrack(int t){
    if(t > n) Output(x);    //搜索至树叶
    else
        for(int i = 1;i<=n;i++)
        {
            x[t] = i;        //在当前扩展结点处X[t]取值可选i
            if(Constraint(t)&&Bound(t))
                Backtrack(t+1);
        }
}

当所给的问题是确定n个元素的满足某种性质的排列时，相应的解空间树称为排列树。

void Backtrack(int t){
    if(t > n) Output(x);    //搜索至树叶
    else
        for(int i = 1;i<=n;i++)
        {
            Swap(x[t],x[i]);
            if(Constraint(t)&&Bound(t))
                Backtrack(t+1);
            Swap(x[t],x[i]);
        }
}

二、N皇后问题

问题描述

n皇后问题要求在一个n：n格的棋盘上放置n格皇后，使得她们彼此不受攻击，一个皇后可以攻击与之同一行或同一列或同一斜线上的其他任何棋子，因此，n皇后问题等价于：任何两个皇后不能再同行、同列、同一斜线上。

算法设计

        对n后问题，可用n元组x[1:n]表示它的解。其中，x[i]表示皇后i放在棋盘的第i行(即，可保证不同的皇后放在不同行)的第x[i]列。

        由于不允许将两个皇后放在同一列，所以解向量中的x[i]互不相同。

        按照对nxn格棋盘的行和列分别从上到下和从左到右编号为1, 2, 3, 4, .... n,从棋盘左上角到右下角的主对角线及其平行线(即斜率为+1的各条斜线)上，各格的两个坐标的差值(行号-列号)相等;斜率为-1的每一条斜线上，各格的两个坐标的和值(行号+列号)相等。所以，若2个皇后放置的位置分别是(i,x[i]) 和(k,x[k])，则约束条件为:

        x[i]≠x[k] (不在同一列)

        i-x[i]≠k-x[k]，且i+x[i]≠k+x[k](不在同一斜线) ，即|i- k|≠x[i]-x[k]|

        用回溯法解n皇后问题时，可用可行性约束函数Place剪去不满足行、列和斜线约束的子树:以深度优先搜索方式递归地对可行子树进行搜索。

int n,x[N+1],sum = 0;//n为皇后个数，x数组记录当前解,sum可行解的个数
boolean Place(int k){//可行性约束函数 
	for(int j = 1;j<k;j++)
		if((abs(k-j)==abs(x[j]-x[k]))||x[j]==x[k])//不满足约束条件
			return FALSE;
	return TRUE; 
} 
void Backtrack(int t){ 
	if(t>n){	//搜索到叶结点，得到可行解 
		sum++;
		for(int i = 1;i<=n;i++)
			cout<<x[i]<<"";
		cout<<endl;
	}
	else
		for(int i = 1;i<=n;i++){
			x[t] = i;
			if(Place(t))//检查当前结点可行性，不满足则回溯 
				Backtrack(t+1);//满足则 向下搜索 
		}
}

时间复杂度

O（n^(n+1)）

三、图的M着色问题

问题描述

若一个图最少需要m种颜色才能使图中任何一条边连接的2个顶点着有不同颜色，则称这个数m为该图的色数。求一个图色数m的问题称为图的m可着色优化问题。

给定一个图G=（V,E）和m种颜色，如果这个图不是m可着色的，就“no”，如果是，则找出所有可着色方法，本问题除了回溯法外，目前无更好的方法。

算法设计

问题的解空间可以表示为高度为n+1的完全m叉树

void Backtrack(int t){
	if(t>n){
		sum++;
		for(int i = 1;i<=n;i++)
			cout<<x[i]<<"";
		cout<<endl;
	}
	else
		for(int i = 1;i<=m;i++){//m表示m种不同颜色 
			x[t] = i;
			if(Ok(t))
				Backtrack(t+1);
		}
} 
boolean Ok(int k){//检查颜色可用性 
	for(int j = 1;j<k;j++)
		if((a[k][j]==1)&&(x[j]==x[k]))//0不相连，1为相连，相连并且颜色相同则不可用 
				return false;
		return true;
}