本文介绍了两种解决NC110旋转数组问题的方法：一是利用取模性质和翻转技巧，通过三次翻转完成元素移动；二是通过模拟循环右移，将数组拆分成环进行独立操作。详细步骤和代码实现有助于理解数组旋转的算法原理。
NC110 旋转数组
题目大意
给出一个长度为 n n n 的一维数组 a r r arr arr，将 a r r arr arr 中的每个元素循环向右移动 m m m 个位置。更严格一点的定义是：将原本在位置 i i i 处的元素移动至 ( i + m ) m o d n (i+m)\bmod n (i+m)modn 处。
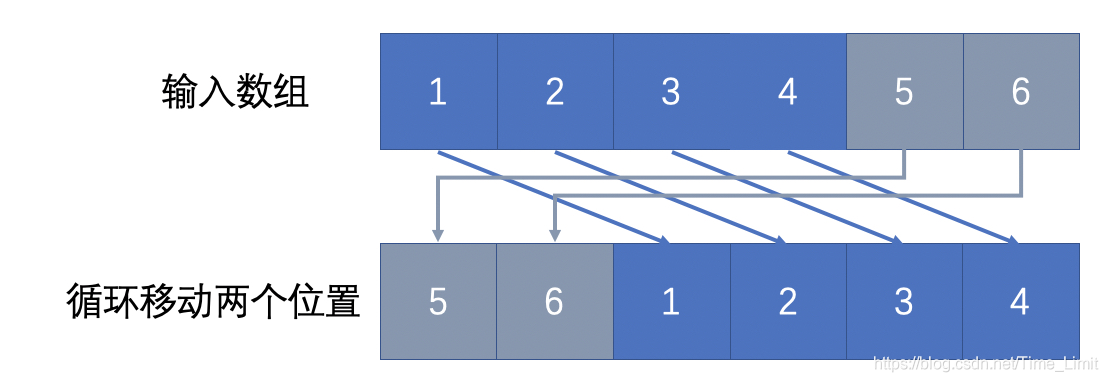
比如，输入为 ( 1 , 2 , 3 , 4 , 5 , 6 ) (1,2,3,4,5,6) (1,2,3,4,5,6)， m = 2 m=2 m=2，操作结果如下图示：
方法一
首先明确一件事情，根据取模运算的分配律可得
( i + m ) m o d n = ( i m o d n + m m o d n ) m o d n = ( i + m m o d n ) m o d n \begin{aligned} (i+m)\bmod n &= (i\bmod n + m\bmod n)\bmod n \\ &= (i + m\bmod n)\bmod n \end{aligned} (i+m)modn=(imodn+
最低0.47元/天 解锁文章
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
