《Probability for Data Science-Chapter_24》翻译

面向数据科学的概率论——第二十四章 简单线性回归

原文：https://nbviewer.jupyter.org/github/prob140/textbook/tree/gh-pages/notebooks/Chapter_24/

译者：ThomasCai

协议：CC BY-NC-SA 4.0

自豪地采用谷歌翻译

00 简单线性回归

在数据科学中，回归模型被广泛地应用于预测。本章从概率论的角度来研究线性最小二乘法。重点是简单回归，即基于一个数值属性的预测。

当属性$X$和响应$Y$的联合分布为二元正态分布时，$(X,Y)$的经验分布是橄榄球的形状，与数字8的非常相似。我们将从相关的几何解释开始，因为这有助于理解回归和二元正态分布。我们要推导的线性回归的方程，可以用几种方法来表示；在本章的末尾，我们将以最容易扩展到多元回归的方式来表示它。

01 二元正态分布

# HIDDEN
from datascience import *
from prob140 import *
import numpy as np
import warnings
import matplotlib.cbook
warnings.filterwarnings("ignore",category=matplotlib.cbook.mplDeprecation)
import matplotlib.pyplot as plt
plt.style.use('fivethirtyeight')
%matplotlib inline
from scipy import stats

# HIDDEN

def sin(theta):
    return np.sin(theta * np.pi/180)
def cos(theta):
    return np.cos(theta * np.pi/180)
def tan(theta):
    return sin(theta)/cos(theta)

def projection_1_2(theta):
    x = 1
    z = 2
    y = x*cos(theta) + z*sin(theta)
    plt.figure(figsize=(6, 6))
    plt.scatter(x, z, s=40, color='green')
    plt.plot([-3, 3], [0, 0], color='grey', lw=2, label=r'$X$'+' axis')
    plt.plot([0, 0], [-3, 3], color='grey', lw=2)
    plt.plot([-3, 3], [tan(theta)*(-3), tan(theta)*3], color='gold', lw=2, label='New axis at positive angle '+r'$\theta$ to the '+r'$X$'+' axis')
    plt.plot([0, x], [0, 0], color='blue', lw=2)
    plt.plot([x, x], [0, z], color='green', linestyle='--', lw=2)
    plt.plot([x, cos(theta)*y], [z, sin(theta)*y], color='green', linestyle='--', lw=2)
    plt.plot([0, cos(theta)*y], [0, sin(theta)*y], color='red', lw=2)         
    plt.axes().set_aspect('equal')
    plt.legend(bbox_to_anchor=(1.92, 1.02))
    plt.xlabel('$X$')
    plt.ylabel('$Z$', rotation=0)
    plt.title('Projection of $(X, Z) = (1, 2)$ on Gold Axis')
    plt.xlim(-3, 3)
    plt.ylim(-3, 3)
    
def projection_trig():
    x = 1
    z = 2
    x1 = x*cos(theta)
    x2 = z*sin(theta)
    y = x1 + x2
    plt.figure(figsize=(8, 8))
    plt.scatter(x, z, s=40, color='green')
    plt.plot([-3, 3], [0, 0], color='grey', lw=2)
    plt.plot([0, 0], [-3, 3], color='grey', lw=2)
    plt.plot([-3, 3], [tan(theta)*(-3), tan(theta)*3], color='gold', lw=2)
    plt.plot([0, x], [0, 0], color='blue', lw=2)
    plt.plot([x, x], [0, z], color='green', linestyle='--', lw=2)
    plt.plot([x, cos(theta)*y], [z, sin(theta)*y], color='green', linestyle='--', lw=2)
    plt.plot([x, cos(theta)*x1], [0, sin(theta)*x1], color='k', linestyle='--', lw=2)
    plt.plot([cos(theta)*y, x+cos(theta)*x2], [sin(theta)*y, sin(theta)*x2], color='k', linestyle='--', lw=2)
    plt.plot([x, x+cos(theta)*x2], [0, sin(theta)*x2], color='k', linestyle='--', lw=2)
    plt.plot([0, cos(theta)*x1], [0, sin(theta)*x1], color='brown', lw=3, label='Length = '+r'$X\cos(\theta)$')
    plt.plot([cos(theta)*x1, cos(theta)*y], [sin(theta)*x1, sin(theta)*y], color='darkblue', lw=3, label='Length = '+r'$Z\sin(\theta)$')
    plt.text(0.3, 0.06, r'$\theta$', fontsize=20)
    plt.text(1.03, 1.6, r'$\theta$', fontsize=20)
    plt.text(0.8, 2.1, r'$(X, Z)$', fontsize=15)
    plt.legend(bbox_to_anchor=(1.35, 1))
    plt.axes().set_aspect('equal')
    plt.xlabel('$X$')
    plt.ylabel('$Z$', rotation=0)
    plt.title('$Y =$ '+r'$X\cos(\theta) + Z\sin(\theta)$')
    plt.xlim(-0.5, 3)
    plt.ylim(-0.5, 3)

二元正态分布

多元正态分布由均值向量和协方差矩阵定义。协方差的单位通常难以理解，因为它们是两个变量的单位的乘积。

将协方差归一化以使其更容易解释是个好主意。正如你们在练习中看到的，对于联合分布的随机变量$X$和$Y$, $X$和$Y$之间的相关性（译者注：相关系数）定义为：
$$\tau {}_X{,}_Y=\frac{Cov(X,Y)}{\sigma {}_X\sigma {}_Y}=E(\frac{X-\mu {}_X}{\sigma {}_X}\cdot \frac{Y-\mu {}_Y}{\sigma {}_Y})=E(X{}^{\ast }Y{}^{\ast })$$

其中$X{}^{\ast }$是标准单位的$X$，$Y{}^{\ast }$是标准单位的$Y$。

相关性的性质

你在练习中可以看到这些。

• $\tau {}_X{,}_Y$只依赖于标准单位，因此它是一个没有单位的纯数
• $\tau {}_X{,}_Y=\tau {}_Y{,}_X$
• $-1\le \tau {}_X{,}_Y\le 1$
• 如果$Y=aX+b$，然后$\tau {}_X{,}_Y$是1或-1，这根据$a$的符号是正还是负。

我们认为$\tau {}_X{,}_Y$衡量了$X$和$Y$的线性关系。

和的方差

重写一下相关性的公式

$$Cov(X,Y)=\tau {}_X{,}_Y\sigma {}_X\sigma {}_Y$$

所以$X+Y$的方差是

$$\sigma {}_{X+Y}^2=\sigma {}_X^2+\sigma {}_Y^2+2\tau {}_{X,Y}{\sigma }_X{\sigma }_Y$$

注意与两个向量之和的长度的公式并行，相关性扮演着两个向量夹角的余弦的角色。如果这个角是90度，那么cos值为0。这对应于相关性也为零，因此随机变量是不相关的。

在$X$和$Y$的联合分布是二元正态分布的情况下，我们将可视化这个想法。

标准二元正态分布

令$X$和$Z$是独立的标准正态变量，即具有均值向量$0$和协方差矩阵等于单位矩阵的二元正态随机变量。 现在确定一个数$\rho$（即希腊字母rho，小写r），使$-1<\rho <1$，并令

$$A=\left[\begin{array}{cc}1& 0\\ \rho & \sqrt{1-\rho {}^2}\end{array}\right]$$

定义一个新的随机变量$Y=\rho X+\sqrt{1-\rho {}^2}Z$，并注意到

$$\left[\begin{array}{c}X\\ Y\end{array}\right]=\left[\begin{array}{cc}1& 0\\ \rho & \sqrt{1-\rho {}^2}\end{array}\right]\left[\begin{array}{c}X\\ Z\end{array}\right]=A\left[\begin{array}{c}X\\ Z\end{array}\right]$$

所以$X$和$Y$是均值向量为$0$和协方差矩阵的二元正态分布。

$$AIA{}^T=\left[\begin{array}{cc}1& 0\\ \rho & \sqrt{1-\rho {}^2}\end{array}\right]\left[\begin{array}{cc}1& \rho \\ 0& \sqrt{1-\rho {}^2}\end{array}\right]=\left[\begin{array}{cc}1& \rho \\ \rho & 1\end{array}\right]$$

我们说$X$和$Y$有标准的二元正态分布，相关性$\rho$。

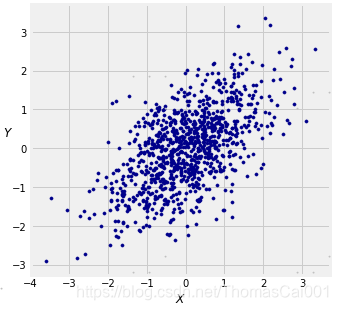
下图显示了在$\rho =0.6$的情况下1000个$(X,Y)$点的经验分布。 您可以改变$rho$的值（译者注：也就是$\rho$）并观察散点图是如何变化的。 它将使您想起数据8中的许多此类模拟。

# Plotting parameters
plt.figure(figsize=(5, 5))
plt.axes().set_aspect('equal')
plt.xlabel('$X$')
plt.ylabel('$Y$', rotation=0)
plt.xticks(np.arange(-4, 4.1))
plt.yticks(np.arange(-4, 4.1))

# X, Z, and Y
x = stats.norm.rvs(0, 1, size=1000)
z = stats.norm.rvs(0, 1, size=1000)
rho = 0.6
y = rho*x + np.sqrt((1-rho**2))*z
plt.scatter(x, y, color='darkblue', s=10);

余弦相关性

我们定义

$$Y=\rho X+\sqrt{1-\rho {}^2}Z$$

其中$X$和$Z$是独立同分布的标准正态变量。
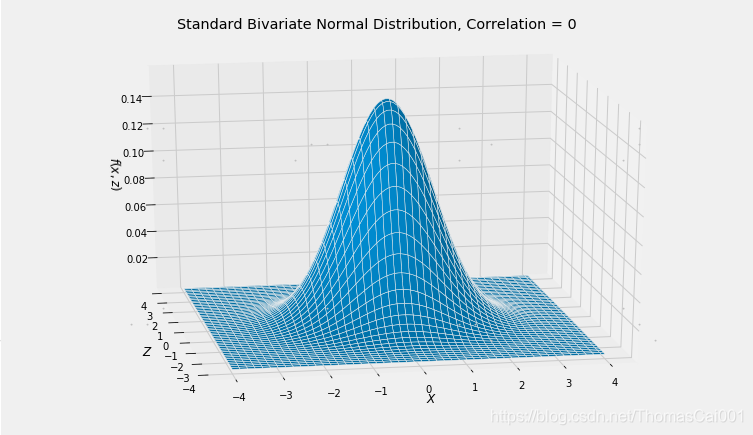
我们从几何上理解这个结构。一个好的起点是$X$和$Z$的联合密度，它具有圆的对称性。

# NO CODE

Plot_bivariate_normal([0, 0], [[1, 0], [0, 1]])
plt.xlabel('$X$')
plt.ylabel('$Z$')
plt.gca().set_zlabel('$f(x, z)$')
plt.title('Standard Bivariate Normal Distribution, Correlation = 0');

$X$轴和$Z$轴是正交的。让我们看看如果我们扭转它们会发生什么。

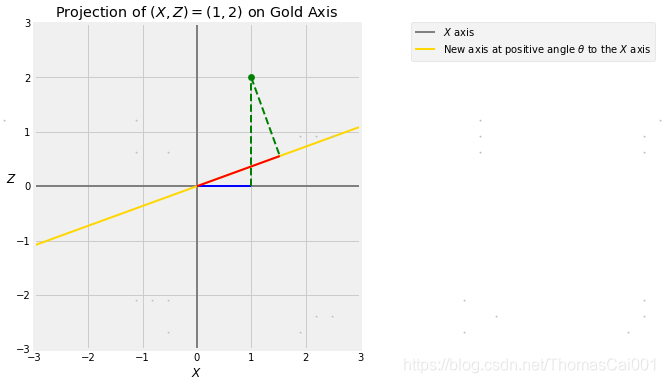
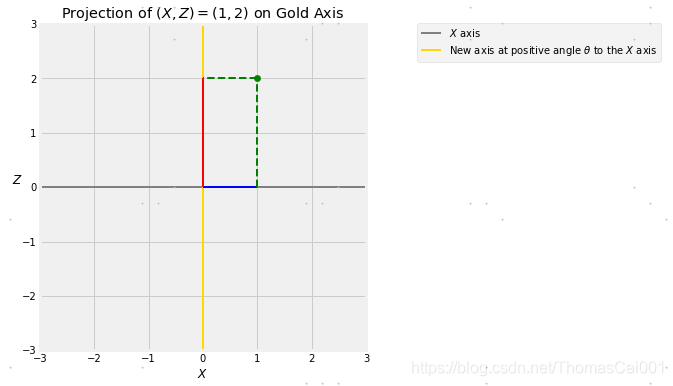
取任何正角度θ度并绘制与原始$X$轴成角度θ的新轴，每个点(X,Z)在这个轴上都有一个投影。

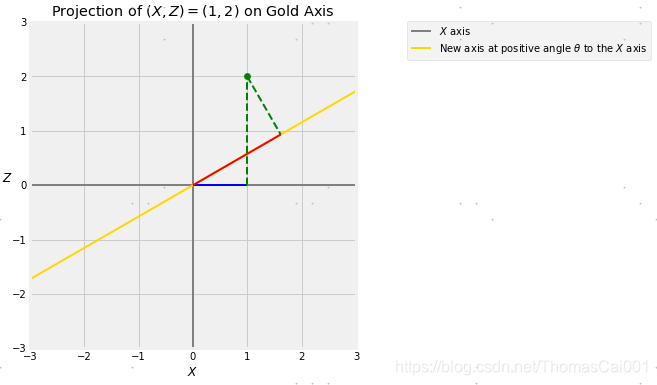
下图所示，点(X,Z)=(1,2)到金色轴的投影，金色轴与$X$轴成θ角。蓝色的部分是$X$的值，通过把(1,2)点向横轴上做垂线得到，称为(1,2)点到横轴上的投影。

红色部分是(1,2)点在金色轴上的投影，通过把(1,2)点向金色轴做垂线得到。

在下面的单元格中改变θ的值，可以观察到投影在金色轴旋转时如何变化。

theta = 20
projection_1_2(theta)

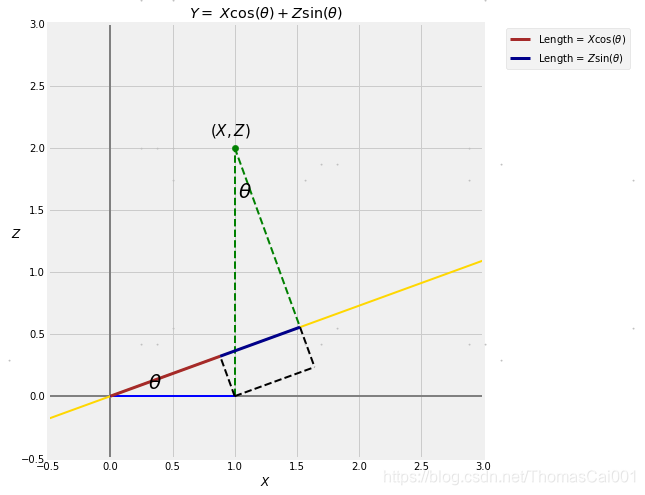
设$Y$是红色段的长度，并记住$X$是蓝色段的长度。 当θ非常小时，$Y$几乎等于$X$。当θ接近90度时，$Y$几乎等于Z。

一点三角法就表明了这一点：$Y=X\cos (\theta )+Z\sin (\theta )$

projection_trig()

因此

$$Y=X\cos (\theta )+Z\sin (\theta )=\rho X+\sqrt{1-\rho {}^2}Z$$

其中$\rho =\cos (\theta )$

下面的一系列图像说明了θ为30度的转换。

theta = 30
projection_1_2(theta)

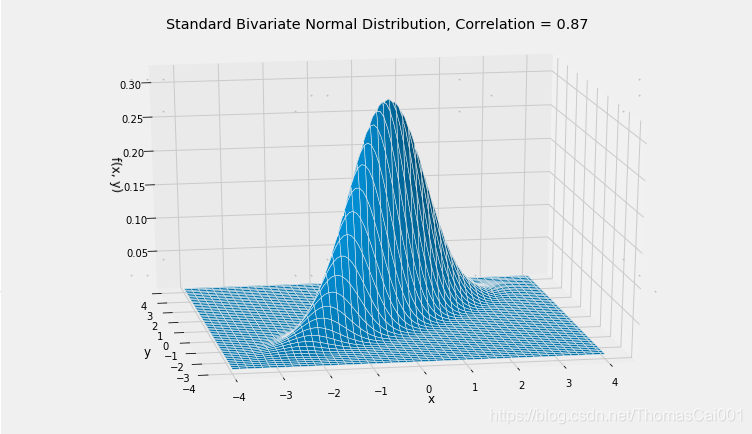
当原始点(X, Z)具有独立同分布的标准正态坐标时，二元正态分布是蓝色和红色长度X和Y的联合分布。此变换(X, Z)的联合密度表面的圆形轮廓成(X, Y)的联合密度表面的椭圆形轮廓。

cos(theta), (3**0.5)/2
>>(0.8660254037844387, 0.8660254037844386)

rho = cos(theta)
Plot_bivariate_normal([0, 0], [[1, rho], [rho, 1]])
plt.title('Standard Bivariate Normal Distribution, Correlation = '+str(round(rho, 2)));

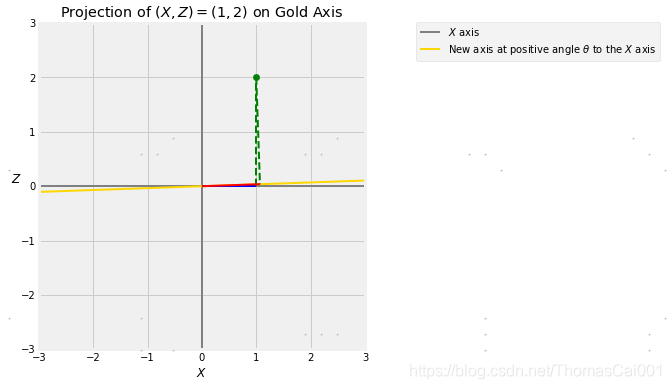
小的θ

正如我们前面看到的，当θ很小，几乎对轴的位置没做任何改变时，X和Y几乎相等。

theta = 2
projection_1_2(theta)

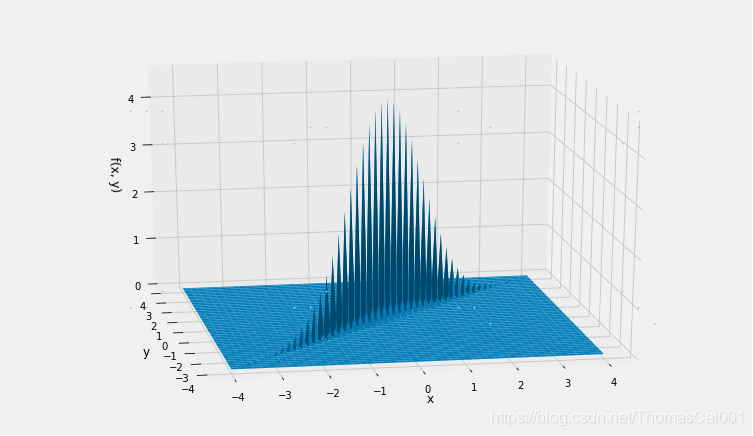
因此，X和Y的二元正态密度本质上受限于X=Y线。cos(θ)的相关性很大因为θ很小；它的值超过0.999。

从而可以看到绘图函数是很难表示这个联合密度面的。

rho = cos(theta)
rho
>>0.99939082701909576

Plot_bivariate_normal([0, 0], [[1, rho], [rho, 1]])

正交性和独立性

当θ是90度，金色轴正交于X轴，并且Y = Z（其中Z与X是独立的）。

theta = 90
projection_1_2(theta)

当θ= 90°时，cos(θ)= 0。(X,Y)的联合密度面与(X,Z)的联合密度面相同，并具有圆的对称性。

如果你把$\rho X$当作“信号”，把$\sqrt{1-\rho {}^2}Z$当作“噪声 ”，那么$Y$可以被认为是一个观察的值“信号加噪声”。在本章剩下的部分中，我们将看看是否能将信号与噪声分开。

二元正态的表示

当我们只处理两个变量X和Y时，矩阵表示通常是不必要的。我们将交替使用以下三种表示。

• $X{}_1$和$X{}_2$是具有$(\mu {}_1,\mu {}_2,\sigma {}_1^2,\sigma {}_2^2,\rho )$参数的二元正态变量
• 标准化变量$X{}_1^{\ast }$和$X{}_2^{\ast }$是标准的二元正态且相关性为$\rho$，那么$X{}_2^{\ast }=\rho X{}_1^{\ast }+\sqrt{1-\rho {}^2}Z$（其中标准正态$Z$与$X{}_1^{\ast }$是相互独立的）。这是由多元正态的定义2得出的。
• $X{}_1$和$X{}_2$有多元正态分布的均值向量$[\mu {}_1\mu {}_2]{}^T$和协方差矩阵
  $$\left[\begin{array}{cc}\sigma {}_1^2& \rho \sigma {}_1\sigma {}_2\\ \rho \sigma {}_1\sigma {}_2& \sigma {}_2^2\end{array}\right]$$

02 线性最小二乘法

# HIDDEN
from datascience import *
from prob140 import *
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('fivethirtyeight')
%matplotlib inline
from scipy import stats

最小二乘线性预测器

在这一节中，我们将远离二元正态分布，看看我们能否基于另一个数字变量的预测因子，从一个数字变量的所有线性预测因子中找出最好的，而不管这两个变量的联合分布如何。

对于联合分布随机变量$X$和$Y$，你知道$E(Y\mid X)$是$Y$基于$X$函数的最小二乘预测器。我们现在将允许的函数限制为线性函数，并且看看我们能否在其中找到最好的一个。下一节我们将看到这个最好的线性预测器，所有预测器中最好的，和二元正态分布之间的联系。

最小化均方误差

令$h(X)=aX+b$其中$a$和$b$为常量，并且使$MSE(a,b)$表示$MSE(h)$
$$MSE(a,b)=E((Y-(aX+b)){}^2)$$
为了找到最小二乘线性预测器，我们必须在所有$a$和$b$上最小化这个MSE。我们将使用微积分分两步完成：

• 固定$a$的值，并且在这个$a$下寻找$b{}_a^{\ast }$值以使得$MSE(a,b)$最小；
• 然后将这个最小化的值$b{}_a^{\ast }$代入$b$，并且最小化$MSE(a,b{}_a^{\ast })$以求出$a$。

步骤一

固定$a$且最小化$MSE(a,b)$以求得$b$

$$MSE(a,b)=E(((Y-aX)-b){}^2)=E((Y-aX){}^2)-2bE(Y-aX)+b{}^2$$

对b求导得

$$\frac{d}{db}MSE(a,b)=-2E(Y-aX)+2b$$

设置此值等于0并求解，可得对于a的固定值的最小化的b值

$$b{}_a^{\ast }=E(Y-aX)=E(Y)-aE(X)$$

步骤二

现在我们最小化以下函数并求得$a$

$$E((Y-(aX+b{}_a^{\ast })){}^2)=E((Y-(aX+E(Y)-aE(X))){}^2)=E\left(\right((Y-E(Y))-a(X-E(X))\left){}^2\right)=E((Y-E(Y)){}^2)-2aE((Y-E(Y))(X-E(X)))+a{}^{2}E((X-E(X)){}^2)=Var(Y)-2aCov(X,Y)+a{}^{2}Var(X)$$

对$a$求导得$-2Cov(X,Y)+2aVar(X)$。所以最小化的$a$是

$$a{}^{\ast }=\frac{Cov(X,Y)}{Var(X)}$$

在这一点上，我们应该检查我们所拥有的是最小值，而不是最大值，但是根据您的预测经验，您可能只愿意接受我们所拥有的最小值。如果不是，那么再次求导，看看得到的函数的符号。

回归线的斜率和截距

最小二乘直线称为回归线。最小二乘直线称为回归线。现在你可以从数据8中得到它的等式的证明。设$\tau {}_X{,}_Y$是$X$和$Y$之间的相关性。然后斜率和截距由下式给出：

$$回归线的斜率=\frac{Cov(X,Y)}{Var(X)}=\tau {}_X{,}_Y\frac{\sigma {}_Y}{\sigma {}_X}$$

$$回归线的截距=E(Y)-斜率\cdot E(X)$$

标准单位的回归

如果$X$和$Y$都是用标准单位测量的，那么回归线的斜率就是相关性$\tau {}_X{,}_Y$，截距为0。

换句话说，已知$X=x$标准单位，Y的预测值为$\tau {}_X{,}_{Y}x$标准单位。当$\tau {}_X{,}_Y$为正而不是1时，这个结果称为回归因子；Y的预测值比X的给定值更接近0。

散点图的线和形状

以上计算表明：

• 回归线经过这个点$(E(X),E(Y))$.
• 不管$X$和$Y$的联合分布如何，回归线的方程都成立。
• 无论$X$和$Y$之间的关系如何，在所有直线中始终存在最佳直线预测器。如果关系不是大致线性的，则不希望使用最佳直线进行预测，因为最佳直线仅仅是一类不好的预测结果中最好， 它总是存在。

03 回归和二元正态分布

# HIDDEN
from datascience import *
from prob140 import *
import numpy as np
import warnings
import matplotlib.cbook
warnings.filterwarnings("ignore",category=matplotlib.cbook.mplDeprecation)
import matplotlib.pyplot as plt
plt.style.use('fivethirtyeight')
%matplotlib inline
from scipy import stats

# HIDDEN 
def bivariate_normal_regression(rho, n):
    x = stats.norm.rvs(size=n)
    z = stats.norm.rvs(size=n)
    y = rho * x  +  (1 - rho**2)**0.5 * z
    plt.scatter(x, y, color='darkblue', s=10)
    if rho >= 0:
        plt.plot([-4, 4], [-4, 4], color='red', lw=2, label='y = x')
    else:
        plt.plot([-4, 4], [4, -4], color='red', lw=2, label='y = -x')
    
    plt.plot([-4, 4], [rho*(-4), rho*(4)], color='green', lw=2, label='Regression Line: y = '+str(rho)+'x')
    
    # Axes, labels, and titles
    plt.xlim(-4, 4)
    plt.ylim(-4, 4)
    plt.axes().set_aspect('equal')
    plt.legend(bbox_to_anchor=(2, 1.02))
    plt.xlabel('$X$')
    plt.ylabel('$Y$', rotation=0)
    plt.title('Standard Bivariate Normal, Correlation '+str(rho))

回归和二元正态

令$X$和$Y$为标准的二元正态变量。且他们的相关性为$\rho$。关系为：

$$Y=\rho X+\sqrt{1-\rho {}^2}Z$$

其中$X$和$Z$是独立的正态分布变量，他们直接导致了基于$X$的所有函数的的$Y$的最佳预测值。显然，最佳的预测为条件期望值$E(Y|X)$。

$$E(Y|X)=\rho X$$

因为$Z$与$X$是独立的，因此$E(Z)=0$。

因为$E(Y|X)$是$X$的一个线性函数，所以我们可以知道：

如果$X$和$Y$有一个标准的二元正态分布，那么基于$X$的$Y$的最佳预测值是线性的，并且有上一节推导的回归方程。

每一个二元正态分布都可以由标准二元正态变量的线性变换来构造。因此：

如果$X$和$Y$是二元正态的，那么基于X的Y的最佳线性预测因子也是基于$X$的$Y$的所有预测结果中最好的。

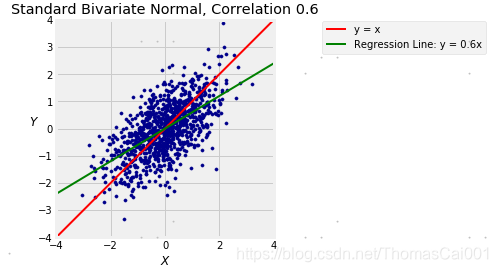
函数bivariate_normal_regression（代码中）以ρ和n为参数并显示由相关性ρ的标准二元正态分布产生的n个点的散点图。它也显示了45度“相同标准单位”线（红色）和$E(Y\mid X)=\rho X$（绿色）。

您在数据8中看到过这样的图，但是无论如何，请运行单元格几次以刷新内存。您可以看到当回归因子ρ> 0时；绿线比红线（“相同标准单位”45度线）更平。

bivariate_normal_regression(0.6, 1000)

预测误差

根据定义，$Y$等于一个“信号”，它是一个$X$的线性函数，再加上一些等于$\sqrt{1-\rho {}^2}Z$的噪声。基于$X$ 的$Y$的最佳预测为线性函数ρX。

这个预测的均方误差是

$$Var(Y|X)=(1-\rho {}^2)Var(Z)=1-\rho {}^2$$

它不依赖于$X$。这是有意义的，因为$Y$定义中的“噪声”项与$X$无关。

垂直带状分布

如果$X$和$Y$是相关性为ρ的标准二元正态变量，上面的计算可以表明，给定$X=x$的Y的条件分布是正态的，平均值为ρx和方差为$\sqrt{1-\rho {}^2}$。

预测排名

假设一大批学生的口语和数学考试成绩的散点图大致为椭圆形，两个变量之间的相关性为0.5。

给定一个随机挑选的口语成绩排在第80分位数的学生，您对这个学生的数学成绩的百分位的预测是什么?

回答这些问题的一种方法是做一些概率假设。对事实的粗糙估计，根据给定的信息，学生的标准化的数学分数$M$和标准化的口语分数$V$有相关性ρ= 0.5的标准二元正态分布。

考虑到学生的口语成绩是在第80分位数上，我们知道他们正处于Python所谓的标准正常曲线的80％点。所以他们的标准单位分数大约是0.84。

standard_units_x = stats.norm.ppf(0.8)
standard_units_x
>>>0.8416212335729143

数学分数标准单位的回归预测是$0.5\times 0.84=0.42$。

rho = 0.5
standard_units_predicted_y = rho * standard_units_x
standard_units_predicted_y
>>>0.42081061678645715

标准正常曲线下左侧0.42的区域约为66％，因此您的预测是学生将达到大约数学分数的第66分位数。

stats.norm.cdf(standard_units_predicted_y)
>>>0.6630533107760167

在这种设置中不要担心小数点和高精度。 计算基于关于数据的概率模型；偏离该模型对预测质量的影响要大于您的答案是第67分位数而不是第66分位数。

但是，您应该注意到，在答案中可以清楚地看到回归因子。学生预测的数学成绩比他们的口语成绩更接近平均水平。

04 回归方程

# HIDDEN
from datascience import *
from prob140 import *
import matplotlib.pyplot as plt
import numpy as np
plt.style.use('fivethirtyeight')
%matplotlib inline
from scipy import stats

回归方程

基于$X$的预测$Y$的回归方程可以用几种等价的方式表示。回归方程和回归估计中的误差最好用标准单位来表示。所有其他的表示都遵循简单的代数。

令$X$和$Y$是二元正态参数$(\mu X,\mu Y,\sigma {}^{2}X,\sigma {}^{2}Y,\rho )$。然后，正如我们所见，最佳预测值$E(Y\mid X)$是$X$的线性函数，因此$E(Y\mid X)$的公式也是回归直线的方程。

标准单位

设$X^{\ast }$为标准单位的$X$， $Y^{\ast }$为标准单位$Y$。回归方程为

$$E(Y^{\ast }|X^{\ast })=\rho X^{\ast }$$

且预测中的误差量通过下式计算

$$SD(Y^{\ast }|X^{\ast })=\sqrt{1-{\rho }^2}$$

条件标准差与预测的单位相同。条件方差是：

$$Var(Y^{\ast }|X^{\ast })=1-{\rho }^2$$

我们知道的不仅仅是条件期望和条件方差。已知给定$X^{\ast }$的$Y^{\ast }$的条件分布是正态的。这使得我们可以通过常规的正态曲线方法，找到给定$X^{\ast }$的条件概率。例如,

$$P(Y{}^{\ast }<y{}^{\ast }|X{}^{\ast }<x{}^{\ast })=\Phi (\frac{y{}^{\ast }-\rho x{}^{\ast }}{\sqrt{1-\rho {}^2}})$$

在高尔顿的一个著名数据集中，父子对的身高分布大致是二元正态分布，其相关系数为0.5。在身高比平均值高出两个标准差的父亲中，儿子身高比平均水平高出两个标准差的比例是多少?

通过回归效应，你知道答案必须小于50%。如果$Y^{\ast }$表示随机选取的儿子的身高(标准单位)，$X^{\ast }$表示他的父亲的身高(标准单位)，则比例近似为

$$P(Y{}^{\ast }>2|X{}^{\ast }=2)=1-\Phi (\frac{2-0.5\times 2}{\sqrt{1-0.5{}^2}})$$

这个值大约是12.4%。

1 - stats.norm.cdf(2, 0.5*2, np.sqrt(1-0.5**2))
>>> 0.12410653949496186

一种原始形式

通常，您想要以测量数据的单位进行预测。在改变上述公式中的单位之前，请记住$X$上的条件等价于$X^{\ast }$上的条件。如果你知道X或者$X^{\ast }$的值，你也知道另一个。

回归方程为

$$E(Y|X)=E(\sigma {}_{Y}Y{}^{\ast }+\mu {}_Y|X)=\sigma {}_{Y}E(Y{}^{\ast }|X)+\mu {}_Y=\sigma {}_Y\rho (\frac{X-\mu {}_X}{\sigma {}_X})+\mu {}_Y=\rho \frac{\sigma {}_Y}{\sigma {}_X}X+(\mu {}_Y-\rho \frac{\sigma {}_Y}{\sigma {}_X}\mu {}_X)$$

这和我们之前推导的最小二乘直线方程是一样的，我们没有对$X$和$Y$的联合分布做任何假设。这证实了我们的观察，如果$X$和$Y$是二元正态的，那么最佳的线性预测器就是所有预测器中最好的。

预测中的误差量由以下两式衡量

$$SD(Y|X)=SD(\sigma {}_{Y}Y{}^{\ast }+\mu {}_Y|X)=\sigma {}_{Y}SD(Y{}^{\ast }|X)=\sqrt{1-\rho {}^2}\sigma {}_Y$$

和

$$Var(Y|X)=(1-\rho {}^2){\sigma }_Y^2$$

给定$X$下的$Y$的条件分布为正态分布，上面计算的是均值和方差。

另一种形式

当只有两个变量时，二元正态的矩阵形式几乎没有必要。但仅用多元正态分布的参数（均值向量和协方差矩阵）就可以写出回归估计和条件方差。这项工作将在下一章中得到反馈，因为完全类似的公式将适用于多元回归。

定义$\rho {}_X{,}_Y=Cov(X,Y)$。那么$X$和$Y$有多元正态分布，其平均向量为$[\mu X,\mu Y]{}^T$和协方差矩阵

$$\left[\begin{array}{cc}\sigma {}_X^2& \sigma {}_X{,}_Y\\ \sigma {}_X{,}_Y& \sigma {}_Y^2\end{array}\right]$$

现在

$$\rho =\frac{\sigma {}_X{,}_Y}{\sigma {}_X\sigma {}_Y}$$

并且回归方程能被写为

$$E(X|Y)=\sigma {}_Y\rho (\frac{X-\mu {}_X}{\sigma {}_X})+\mu {}_Y=\frac{\sigma {}_X{,}_Y}{\sigma {}_X^2}(X-\mu {}_X)+\mu {}_Y=\sigma {}_Y{,}_X(\sigma {}_X^2){}^{-1}(X-\mu {}_X)+\mu {}_Y$$

同时

$$\rho {}^2=\frac{{\sigma }_{X,Y}^2}{\sigma {}_X^2\sigma {}_Y^2}$$

所以误差的方差为

$$Var(Y|X)=(1-\rho {}^2)\sigma {}_Y^2=\sigma {}_Y^2-{\sigma }_{X,Y}^2(\sigma {}_X^2){}^{-1}=\sigma {}_Y^2-{\sigma }_{Y,X}(\sigma {}_X^2){}^{-1}{\sigma }_{X,Y}$$