机器学习之深入理解矩阵求导的基本方法

一、分子布局、分母布局

前提： 若 x 为向量，则默认 $x$ 为列向量， $x^T$ 为行向量

布局简单地理解就是分子 y 、分母 x 是行向量还是列向量。

• 分子布局（Numerator-layout）： 分子为 $y$ 或者分母为 $x^T$(即分子为列向量或者分母为行向量)
• 分母布局（Denominator-layout）： 分子为 $y^T$ 或者分母为 $x$(即分子为行向量或者分母为列向量)

1. 分子布局

• 标量/向量：
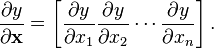  （分子为标量，分母的向量为行向量）

• 向量/标量：
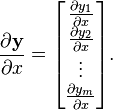  （分子的向量为列向量，分母为标量）

• 向量/向量：
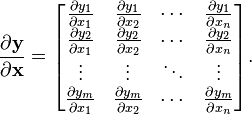  （分子为列向量横向平铺，分母为行向量纵向平铺）

• 标量/矩阵：
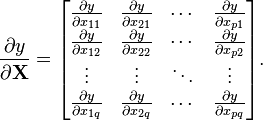  （分子为标量，分母为矩阵的转置）

• 矩阵/标量：
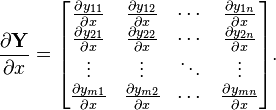  （分子为矩阵的转置，分母为标量）

2. 分母布局

• 标量/向量：
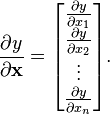  （分子为标量，分母的向量为列向量）

• 向量/标量：
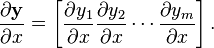  （分子的向量为行向量，分母为标量）

• 向量/向量：
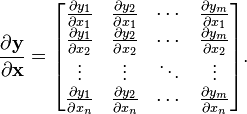  （分子为行向量纵向平铺，分母为列向量横向平铺）

• 标量/矩阵：
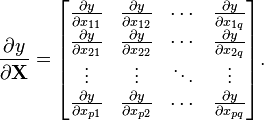  （分子为标量，分母的矩阵为原始矩阵）

二、几个重要的定义

定义1、梯度（Gradient）

设$f(x)$是一个变量为$x$的标量函数，其中$x=(x_1...x_N{)}^T$。那么定义$f(x)$对$x$的梯度为$\frac{df(x)}{dx}$：

梯度的转置是一个行向量：

定义2. 海塞矩阵（Hessian matrix）

设$f(x)$是一个二阶可微分的标量函数，其中$x=(x_1...x_N{)}^T$。那么定义$f(x)$对$x$的海塞矩阵为$\frac{d^{2}f(x)}{dxd{x}^T}$：

定义3. 雅可比矩阵（Jacobian matrix）

设$f(x)$是一个K x 1的列向量函数

其中$x=(x_1...x_L{)}^T$。那么定义$f(x)$对$x$的雅可比矩阵为$\frac{df(x)}{d{x}^T}$：

定义4. 矩阵对标量微分

M × N的矩阵$A$的元素是一个向量$x$的元素$x_q$的函数，定义$\frac{\partial A}{\partial x_q}$为：

矩阵的二阶微分：

三、矩阵迹的微分（Derivative of Traces）

在机器学习中，有时候需要对一个矩阵的F模进行微分，而矩阵的F是可以转换为矩阵的迹，矩阵的迹的微分的计算可以帮助我们计算矩阵的F模的微分。矩阵的F模和迹的关系：

其中$A^{\ast }$是$A$的共轭转置。矩阵的迹的性质：

$$\frac{\partial }{\partial x}\mathrm{tr}(F(x))=f(x{)}^T$$

其中，$f()$是$F()$的微分。

一阶：

二阶：

高阶：

如果想要更多的资源，欢迎关注 @我是管小亮，文字强迫症MAX~

回复【福利】即可获取我为你准备的大礼，包括C++，编程四大件，NLP，深度学习等等的资料。

想看更多文（段）章（子），欢迎关注微信公众号「程序员管小亮」~

参考文章：

• 矩阵、向量微分计算
• 维基百科 Matrix calculus