机器学习之深入理解凸优化次梯度算法

什么是次梯度？并不是很懂，就抽了一些时间，查了资料（很多资料来自百度百科），总结整理了这个博文，记录下自己的学习过程。

0、前言

次梯度方法(subgradient method)是传统的梯度下降方法的拓展，用来处理不可导的凸函数。它的优势是比传统方法处理问题范围大，劣势是算法收敛速度慢。但是，由于它对不可导函数有很好的处理方法，所以学习它还是很有必要的。

1、导数(Derivative)

导数（Derivative），也叫导函数值。又名微商，是微积分中的重要基础概念。导数是函数的局部性质。一个函数在某一点的导数描述了这个函数在这一点附近的变化率。导数的本质是通过极限的概念对函数进行局部的线性逼近。

对于一般的函数$f(x)$，在点$x_0$处的导数为：
$$f^{\prime }(x)=\underset{\Delta x\to 0}{\lim }\frac{\Delta y}{\Delta x}=\underset{\Delta x\to 0}{\lim }\frac{f\left(x_0+\Delta x\right)-f\left(x_0\right)}{\Delta x}$$
等同于
$$f^{\prime }(x)=\underset{\Delta x\to 0}{\lim }\frac{f(x+\Delta x)-f(x)}{\Delta x}=\underset{\Delta x\to 0}{\lim }\frac{f(x)-f(x-\Delta x)}{\Delta x}$$
如果不使用增量，$f(x)$在$x_0$处的导数 也可以定义为：当定义域内的变量$x$趋近于$x_0$时，
$$f^{\prime }(x)=\frac{f(x)-f\left(x_0\right)}{x-x_0}$$

2、次导数(subderivative)

次导数、次切线和次微分的概念出现在凸分析，也就是凸函数的研究中。

设$f:I\to R$是一个实变量凸函数，定义在实数轴上的开区间内。这种函数不一定是处处可导的，例如最经典的例子就是$f(x)=|x|$，在$x=0$处不可导。但是，从下图的可以看出，对于定义域内的任何$x_0$，我们总可以作出一条直线，它通过点$(x_0,f(x_0))$，并且要么接触f的图像，要么在它的下方。直线的斜率称为函数的次导数，次导数的集合称为函数$f$在$x_0$处的次微分。

3、次微分(subdifferential)

凸函数$f:I\to R$在点$x_0$的次导数，是实数$c$使得：
$$f(x)-f\left(x_0\right)\ge c\left(x-x_0\right)$$
对于所有$I$内的$x$。我们可以证明，在点$x_0$的次导数的集合是一个非空闭区间 [a, b]，其中$a$和$b$是单侧极限
$$a=\underset{x\to x_0^{-}}{\lim }\frac{f(x)-f\left(x_0\right)}{x-x_0}$$
$$b=\underset{x\to x_0^{+}}{\lim }\frac{f(x)-f\left(x_0\right)}{x-x_0}$$
它们一定存在，且满足$a\le b$。所有次导数的集合 [a,b] 称为函数$f$在$x_0$的次微分。

例子：考虑凸函数$f(x)=|x|$。在原点的次微分是区间 [−1, 1]。$x_0<0$时，次微分是单元素集合 {-1}，而$x_0>0$，则是单元素集合{1}。

4、次梯度(subgradient)

在优化问题中，我们可以对目标函数为凸函数的优化问题采用梯度下降法求解，但是在实际情况中，目标函数并不一定光滑、或者处处可微，这时就需要用到次梯度下降算法。

次梯度与梯度的概念类似，凸函数的$First-ordercharacterization$是指如果函数$f$可微，那么当且仅当$dom(f)$为凸集，且对于$\forall x,y\in dom(f)$，使得$f(y)\ge f(x)+\nabla f(x{)}^T(y-x)$，则函数$f$为凸函数。这里所说的次梯度是指在函数$f$上的点$x$满足以下条件的$g\in R^n$：
$$f(y)\ge f(x)+g^T(y-x)$$
其中，函数$f$不一定要是凸函数，非凸函数也可以，即对于凸函数或者非凸函数而言，满足上述条件的$g$均为函数在该点的次梯度。但是，凸函数总是存在次梯度（可以利用epigraph和支撑平面理论证明），而非凸函数则不一定存在次梯度，即使$f$可微。该定义说明，用次梯度对原函数做出的一阶展开估计总是比真实值要小。

很明显，凸函数的次梯度一定存在，如果函数$f$在点$x$处可微，那么$g=\nabla f(x)$，为函数在该点的梯度，且唯一；如果不可微，则次梯度不一定唯一。但是对于非凸函数，次梯度则不一定存在，也不一定唯一。

例如，凸函数$\Vert x{\Vert }_p$范数为凸函数，但不满足处处可微的条件，因此，函数的次梯度不一定唯一，如下图：

• 左图为$\Vert x{\Vert }_2$，函数在$x\ne 0$时，次梯度唯一，且$g=x/\Vert x{\Vert }_2$；当$x=0$时，次梯度为$z:\Vert z{\Vert }_2\le 1$中的任意一个元素；

• 右图为$\Vert x{\Vert }_1$，函数在$x\ne 0$时，次梯度唯一，且$g=sign(x)$；当$x=0$时，次梯度为 [−1,1] 中的任意一个元素；

同样，绝对值函数$f(x)=\mid x\mid$和最大值函数 f ( x ) = m a x { f 1 ( x ) , f 2 ( x ) } f(x)=max\{f_1(x),f_2(x)\} f(x)=max{f1​(x),f2​(x)}在不可微点处次梯度也不一定唯一，如下图：

• 左函数为绝对值函数$f(x)=\mid x\mid$，其在满足$x=0$的点处，次梯度为任意一条直线，在向量$\nabla f_1(x)$和$\nabla f_2(x)$之间。；
• 右函数为最大值函数 f ( x ) = m a x { f 1 ( x ) , f 2 ( x ) } f(x)=max\{f_1(x),f_2(x)\} f(x)=max{f1​(x),f2​(x)}，其在满足$f_1(x)=f_2(x)$的点处，次梯度为任意一条直线，在向量$\nabla f_1(x)$和$\nabla f_2(x)$之间。

5、次梯度的性质

• Scalingf：$\partial (af)=a\cdot \partial f$；
• Addition：$\partial (f_1+f_2)=\partial f_1+\partial f_2；$
• Affine composition：$如果g(x)=f(Ax+b)，那么\partial g(x)=A^T\partial f(Ax+b)；$
• Finite pointwise maximum：$如果f(x)={\max }_{i=1,\dots ,m}{f}_i(x)，那么\partial f(x)=\mathrm{conv}\left({\bigcup }_{i:f_i(x)=f(x)}\partial f_i(x)\right)；$

6、灵魂一问：为什么要计算次梯度？

对于光滑的凸函数而言，我们可以直接采用梯度下降算法求解函数的极值，但是当函数不处处光滑，处处可微的时候，梯度下降就不适合应用了。因此，我们需要计算函数的次梯度。对于次梯度而言，其没有要求函数是否光滑，是否是凸函数，限定条件很少，所以适用范围更广。

次梯度具有以下优化条件：对于任意函数$f$（无论是凸还是非凸），函数在点$x$处取得最值等价于：
$$f\left(x^{\ast }\right)=\underset{x}{\min }f(x)\iff 0\in \partial f\left(x^{\ast }\right)$$
即，当且仅当$0$属于函数$f$在点$x^{\ast }$处次梯度集合的元素时，$x^{\ast }$为最优解。

证明：当次梯度$g=0$时，对于所有$y\in dom(f)$，存在$f(y)\ge f(x^{\ast })+0^T(y-x^{\ast })=f(x^{\ast })$，所以，$x^{\ast }$为最优解，即证。

7、次梯度算法(Subgradient method)

次梯度算法与梯度下降算法类似，仅仅用次梯度代替梯度，记$f:{\mathbb{R}}^n\to \mathbb{R}$为定义在${\mathbb{R}}^n$上的凸函数，即：
$$x^{(k+1)}=x^{(k)}-{\alpha }_k{g}^{(k)},k=1,2,3,\dots$$
其中$g^{(k)}$表示函数$f$在$x^{(k)}$的次梯度。如果$f$可微，它的次梯度就是梯度向量$\nabla f$。有时，$-g^{(k)}$不是函数$f$在$x^{(k)}$的下降方向。因此采用一系列可能的$f_{best}$来追踪目标函数的极小值点，即
$$f_{\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}}^{(k)}=\min \left\{f_{\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}}^{(k-1)},f\left(x^{(k)}\right)\right\}$$
另一点与梯度下降算法不同的是：次梯度算法没有明确的步长选择方法，类似Exact line search和Backtracking line search的方法，只有步长选择准则，具体如下：

8、次梯度算法实例

A. Regularized Logistic Regression

对于逻辑回归的代价函数可记为：
$$f(\beta )=\sum _{i=1}^n\left(-y_i{x}_i^T\beta +\log \left(1+\exp \left(x_i^T\beta \right)\right)\right)$$
明显，上式是光滑且凸的，而正则化则是指优化目标函数为：
$$\underset{\beta \in {\mathbb{R}}^p}{\min }f(\beta )+\lambda \cdot P(\beta )$$
如果$P(\beta )=\Vert \beta {\Vert }_2^2$，则成为岭回归（ridge problem），如果$P(\beta )=\Vert \beta {\Vert }_1$则称为Lasso。对于岭回归，我们仍然可以采用梯度下降算法求解目标函数，因为函数处处可导光滑，而Lasso问题则无法用梯度下降算法求解，因为函数不是处处光滑，具体可参考下面的图，所以，对于Lasso问题需要选用次梯度算法求解。

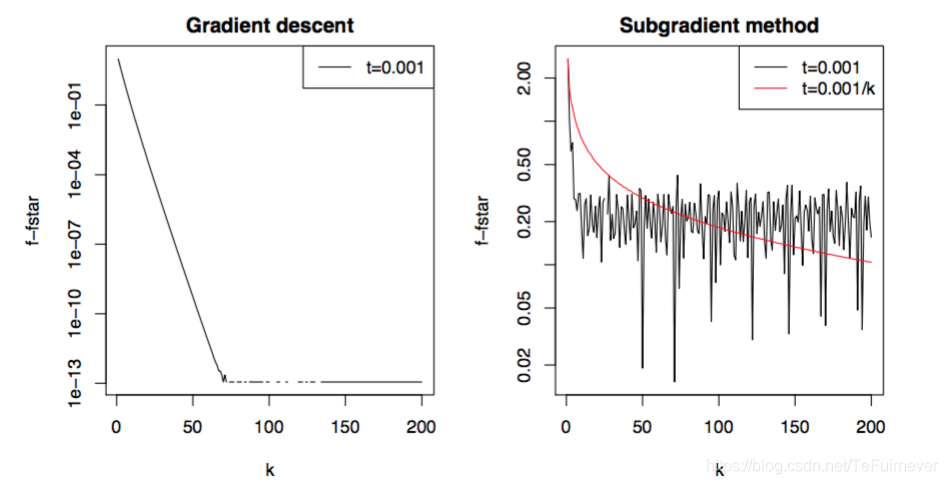
下图是对于同样数据集下分别对逻辑回归选用岭惩罚和Lasso惩罚求解最优解的实验结果图$（n=1000,p=20）$：

B. 随机次梯度算法

随机次梯度算法（Stochastic Subgradient Method）与次梯度算法(Subgradient Method)相比，每次更新次梯度是根据某一个样本计算获得，而不是通过所有样本更新次梯度。

所以，根据梯度更新的方式不同，次梯度算法和梯度下降算法一般被称为“batch method”。从计算量来讲，$m$次随机更新近似等于一次batch更新，二者差别在于${\sum }_{i=1}^m\left[\nabla f_i\left(x^{(k+i-1)}\right)-\nabla f_i\left(x^{(k)}\right)\right]$，当$x$变化不大时，差别可以近似等于0。

对于随机更新次梯度，一般随机的方式有两种：

• Cyclic rule：选择$i_k=1,2,\dots ,m,1,2,\dots ,m,\dots$；
• Randomized rule：均匀随机从$1,\dots ,m$选取一点作为$i_k$。

与所有优化算法一样，随机次梯度算法能否收敛？

答案是肯定的，这里就不在做证明，有兴趣的同学可以参考boyd教授的论文，这里仅给出收敛结果，如下：
$$\underset{k\to \infty }{\lim }f\left(x_{best}^{(k)}\right)\le f^{\ast }+\frac{5m^2{G}^{2}t}{2}$$
对于Cyclic rule，随机次梯度算法的收敛速度为$O(m^3{G}^2/{ϵ}^2)$；对于Randomized rule，随机次梯度算法的收敛速度为$O(m^2{G}^2/{ϵ}^2)$。

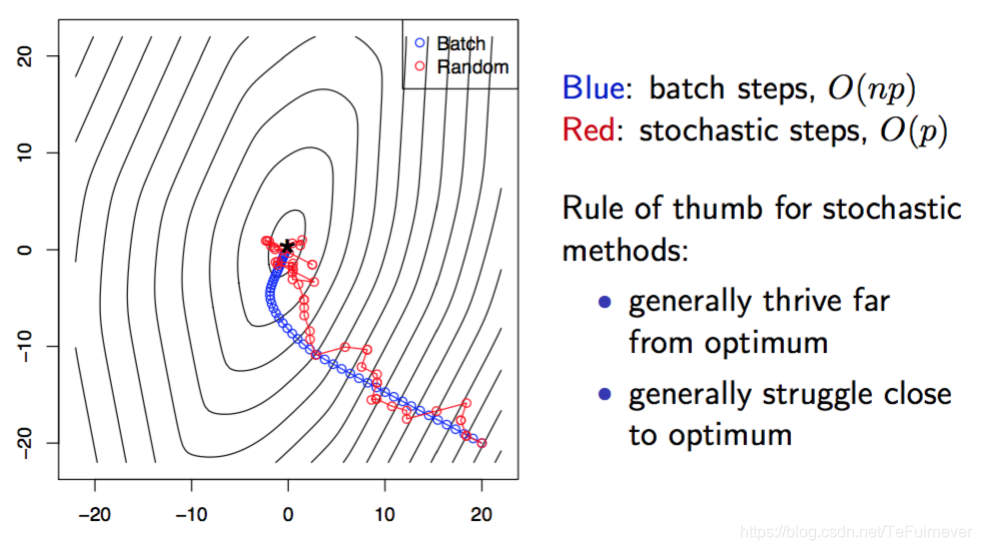
下图给出梯度下降和随机梯度下降算法在同一数据下迭代结果：

如果想要更多的资源，欢迎关注 @我是管小亮，文字强迫症MAX~

回复【福利】即可获取我为你准备的大礼，包括C++，编程四大件，NLP，深度学习等等的资料。

想看更多文（段）章（子），欢迎关注微信公众号「程序员管小亮」~

参考文章

• 百度百科——次梯度方法(subgradient method)
• 百度百科——导数（Derivative）
• 百度百科——次导数
• 凸优化-次梯度算法