LeetCode 1008 Construct Binary Search Tree from Preorder Traversal (dfs)

最新推荐文章于 2025-12-20 23:56:26 发布

原创最新推荐文章于 2025-12-20 23:56:26 发布 · 151 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#leetcode

Leetcode Medium 同时被 2 个专栏收录

244 篇文章

订阅专栏

dfs/bfs

16 篇文章

订阅专栏

本文解析了如何通过给定的整数先序遍历序列，利用递归策略重建二叉搜索树。重点讲解了查找插入位置的二分搜索法，并提供了Java代码示例。理解这个过程对于解决LeetCode上的相关问题至关重要。

Given an array of integers preorder, which represents the preorder traversal of a BST (i.e., binary search tree), construct the tree and return its root.

It is guaranteed that there is always possible to find a binary search tree with the given requirements for the given test cases.

A binary search tree is a binary tree where for every node, any descendant of Node.left has a value strictly less than Node.val, and any descendant of Node.right has a value strictly greater than Node.val.

A preorder traversal of a binary tree displays the value of the node first, then traverses Node.left, then traverses Node.right.

Example 1:

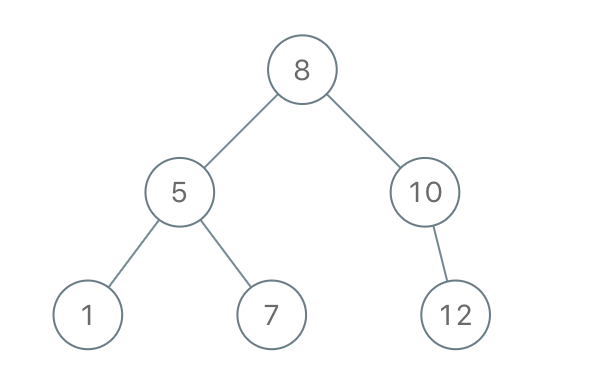
Input: preorder = [8,5,1,7,10,12]
Output: [8,5,10,1,7,null,12]

Example 2:

Input: preorder = [1,3]
Output: [1,null,3]

Constraints:

1 <= preorder.length <= 100
1 <= preorder[i] <= 108
All the values of preorder are unique.

题目链接：https://leetcode.com/problems/construct-binary-search-tree-from-preorder-traversal/

题目大意：根据先序遍历结果恢复二叉搜索树

题目分析：二分找到大于当前根的最小值的下标，然后再分情况二分建树

0ms，时间击败100%

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    
    private int bsearch(int[] a, int l, int r, int val) {
        int mid = 0, ans = -1;
        while (l <= r) {
            mid = (l + r) >> 1;
            if (a[mid] > val) {
                r = mid - 1;
                ans = mid;
            } else {
                l = mid + 1;
            }
        }
        return ans;
    } 
    
    public void solve(TreeNode root, int[] preorder, int l, int r) {
        if (l > r || root == null) {
            return;
        }
        int rp = bsearch(preorder, l, r, root.val);
        root.right = rp == -1 ? null : new TreeNode(preorder[rp]);
        root.left = (rp != -1 && l >= rp) ? null : new TreeNode(preorder[l]);

        solve(root.left, preorder, l + 1, rp == -1 ? r : rp - 1);
        solve(root.right, preorder, rp + 1, r);
    }
    
    public TreeNode bstFromPreorder(int[] preorder) {
        TreeNode root = new TreeNode(preorder[0]);
        solve(root, preorder, 1, preorder.length - 1);
        return root;
    }
}