SVM 支持向量机 推导过程 软硬间隔最大化 线性SVM到非线性SVM 核函数 SMO 三种模型推导证明过程 （Ⅰ）

（一）支持向量机的思想

其实这个模型是为了解决分类问题。而且是基于线性模型的。
我们从最简单的二分类问题入手。
先定义数据集：
T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) . . . ( x N , y N ) } T=\left\{\left(x_1,y_1\right),\left(x_2,y_2\right)...\left(x_N,y_N\right)\right\} T={(x1​,y1​),(x2​,y2​)...(xN​,yN​)}
T = { ( x i , y i ) }          ( i = 1 , 2... N ) T=\left\{\left(x_i,y_i\right)\right\}\;\;\;\;(i=1,2...N) T={(xi​,yi​)}(i=1,2...N)
其中，x是n维的特征向量，y是分类情况用 +1 ， -1 表示。
{ x i ∈ X ⊑ R n y i ∈ Y = { + 1 , − 1    } \left\{\begin{array}{l}x_i\in X\sqsubseteq\mathbb{R}^n\\\\y_i\in Y=\{+1,-1\;\}\end{array}\right. ⎩⎨⎧​xi​∈X⊑Rnyi​∈Y={+1,−1}​
上面我们的工作是把我们的数据集用数学语言表达出来了。现在我们把我们的目标用数学语言表达出来：
首先，要引入最大间隔分类这个问题，其实这个问题我们很早就碰到的了，但是没有细思。

当我们在学习感知机的时候，当时的问题也是分类，但是我们最终分出来的$\omega$参数是和我们第一次选取的随机初始值有关的，也就是说 在感知机中，我们分类的决策限界不是唯一的。对于分类问题 我有很多种分法：

最大间隔分类器的提出：其实就是为了解决在这堆分类方法中选择一个最好的情况。

从直觉上来说我们看两个例子：


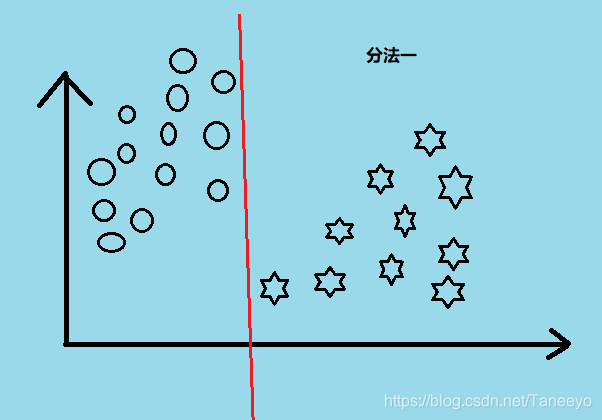
图比较丑，将就看把。按照直觉我们会觉得分法二比较好，因为感觉给人很舒适的感觉。分法一会给人一种很勉强的感觉。其实这里我的理解是 分法二可以保证更高的准确度，可以细思，想想就清楚了。

而这种直觉在数学上是可以定义出来的，它在数学角度上就是一种最大的间隔。我们只要把两个分类之间的那个间隔设置为最大，即为最优的那种分类。
用数学语言表达：
$$goal：max（margin）$$
间隔用margin表示，啊，同时别忘了我们的假设函数：
$$h(x;w)=w^{T}x+b$$
现在把我们的假设函数，和我们要寻找的最大间隔这个目标结合起来。首先$w^{T}x+b=0$ 这个表示决策界限，可以理解的话继续：

这个 $margin$ 从图中来看是可以用N个的对吧，因为对于每个点$x_i$到决策界限都会有一个距离，这个距离的二倍就是$margi{n}_i$ 但是，我们用不了这么多$margin$，不是不想用，其实是用不了，比如我随便找一个$margin$

我们可以看到，在间隔里面已经有一些样本点了。这是不行的。我们目的就是要找一个有宽度的界限能够最大分开这些点。现在我们说的是硬间隔（之后解释），所以说要找的$margin$只能从距离决策限界最近的那个点来做。
$$\begin{gathered} margin=min（x_i到wx+b=0的距离的2倍） \\ margin=min（\frac{2|wx+b|}{\parallel w\parallel }) \end{gathered}$$
结合刚刚的目标有：
$$\begin{gathered} goal：max（margin） \\ goal：maxmin（\frac{2|wx+b|}{\parallel w\parallel }） \end{gathered}$$

（二） 决策函数的粗略推导

现在完善一下我们的表达：
$$\begin{gathered} goal：\underset{w,b}{\max }（margin） \\ goal：\underset{w,b}{\max }\underset{i=1...N}{\min }（2\frac{|w{x}^{(i)}+b|}{\parallel w\parallel }） \end{gathered}$$
同时别忘了线性可分的约束：（我们这一切工作都是建立在数据集线性可分的角度上的，所以约束别忘了）$$y_i(w{x}_i+b)\ge 0$$

发现分母L2范数是和i无关的，可以提出来：
$$goal：\underset{w,b}{\max }\frac{2}{\parallel w\parallel }\underset{i=1...N}{\min }|w{x}^{(i)}+b|$$

现在有个不好理解的问题了，现在函数间隔$|w{x}^{(i)}+b|$的取值是不影响我们这个max求解过程的解。事实上，我们假设将$\omega$和b按比例缩放：$\lambda \omega$ $\lambda b$这时，函数间隔$|w{x}^{(i)}+b|=\lambda |w{x}^{(i)}+b|$。这个对我们的之前那个约束不等式是没有影响的，对目标函数优化也没有影响呢。所以，为了我们计算方便，把它 即 $min|w{x}^{(i)}+b|$ 设为 1 。

则有：
（注意这里我们假设以后，约束项会大于等于1而不是0）
$$\{\begin{array}{l}\underset{w，b}{\max }\frac{2}{\parallel w\parallel }\\ \\ s.t.y_i(w^T{x}_i+b)\ge 1\end{array}$$
我们给它变型：
$$\Rightarrow \{\begin{array}{l}\underset{w，b}{\min }\frac{1}{2}\parallel w{\parallel }^2\\ \\ s.t.y_i(w^T{x}_i+b)-1\ge 0\end{array}$$
如果有数学基础的话，就可以明显看出这是一个凸二次优化问题。或是说凸二次规划问题。

通过求解这个凸优化问题，我们会得到参数 $\stackrel{\wedge }{w}，\stackrel{\wedge }{b}$ 由此可以得到分离超平面：
$$\stackrel{\wedge }{w}x+\stackrel{\wedge }{b}=0$$
以及我们的决策函数：
$$h(x;w,b)=sign(\stackrel{\wedge }{w}x+\stackrel{\wedge }{b})$$
(注：w和x应该是点乘，也就是内积。为了简洁我没有加转置符号)

结论：
我们得到的决策函数是唯一的，也就是说，给我一个线性可分的数据集，那么有个最大间隔分离的超平面是存在且唯一的。我们可以用它做很好的分类，通常比感知机要nb得多。

$$-$$

（三）细化推导过程 利用拉格朗日对偶性 及KKT条件 完善推导

上面到达凸优化的时候，$\stackrel{\wedge }{w}，\stackrel{\wedge }{b}$这两个参数我们其实是没有解出来，上面只是说说推导思路嘛，现在才是怎么把$\stackrel{\wedge }{w}，\stackrel{\wedge }{b}$他们具体的值求出来的过程。

这里的步骤可能需要一些数学知识，不然可能很难理解。关于数学知识部分，之后有空了另外写几篇数学基础的理解。现在就默认已经有这些知识的情况进行推导。

刚刚到了这一步：
$$\Rightarrow \{\begin{array}{l}\underset{w，b}{\min }\frac{1}{2}\parallel w\parallel \\ \\ s.t.y_i(w^T{x}_i+b)-1\ge 0\end{array}$$
现在构建拉格朗日函数：
$$L(w,b,\lambda )=\frac{1}{2}\parallel w\parallel -\sum _{i=1}^N{\lambda }_i{y}_i(w{x}_i+b)+\sum _{i=1}^N{\lambda }_i$$

可以这样理解，对于带约束的情况：
$$\{\begin{array}{l}\underset{w,b}{\min }\frac{1}{2}\parallel w\parallel \\ \\ s.t.y_i(w{x}_i+b)\ge 1\end{array}$$
现在我们再把L函数整理得到：

$$L(w,b,\lambda )=\frac{1}{2}\parallel w\parallel +\sum _{i=1}^N{\lambda }_i(1-y_i(w{x}_i+b))$$
重点看$(1-y_i(w{x}_i+b))$这个式子。

$$\cdot 当(1-y_i(w{x}_i+b))>0时,由于\lambda 是大于0的，因此L(w,b,\lambda )的max也即是最大值，是发散的，趋近无穷$$
$$\begin{gathered} \cdot 当(1-y_i(w{x}_i+b))\le 0时,由于\lambda 是大于0的， \\ 因此maxL(w,b,\lambda )，不是发散的，这个max是存在的 \end{gathered}$$
这个其实也很好理解，maxL（w,b$\lambda$）中有一项是$\lambda$和$(1-y_i(w{x}_i+b))$这个式子的乘积，在第二种情况中，这个乘积是小于0的数，也就是说$\lambda (1-y_i(w{x}_i+b))\le 0$。这时$maxL(w,b,\lambda )$最大值就是当$\lambda =0$,$(1-y_i(w{x}_i+b))=0$ 时。

写整齐一点就是：
$$\{\begin{array}{l}\underset{\lambda }{\max }L(w,b,\lambda )=\infty if(1-y_i(w{x}_i+b))>0\\ \underset{\lambda }{\max }L(w,b,\lambda )=\frac{1}{2}\parallel w\parallel if(1-y_i(w{x}_i+b))=0\\ \underset{\lambda }{\max }L(w,b,\lambda )=Qif(1-y_i(w{x}_i+b))<0(Q<\frac{1}{2}\parallel w\parallel )\end{array}$$
整理得到：
$$\{\begin{array}{l}\underset{\lambda }{\max }L(w,b,\lambda )=\infty if(1-y_i(w{x}_i+b))>0\\ \underset{\lambda }{\max }L(w,b,\lambda )=\frac{1}{2}\parallel w\parallel if(1-y_i(w{x}_i+b))\le 0\end{array}$$
现在把我们原问题拿过来比对：
$$\{\begin{array}{l}\underset{w,b}{\min }\frac{1}{2}\parallel w\parallel \\ \\ s.t.y_i(w{x}_i+b)\ge 1\end{array}$$
正好就是刚刚上面推导式子的第二种情况对吧。
所以整理后

我们的目标转变为求：
$$\{\begin{array}{l}\underset{w,b}{\min }\underset{\lambda }{\max }L(w,b,\lambda )\\ \\ s.t.{\lambda }_i\ge 0\end{array}$$
这一步就是从对w，b的约束到 无对w，b约束 的转换。

由因为二次凸优化问题是强对偶关系：

（minmax问题=maxmin问题，有定理，可以证明的，这里略过）

我们的目标转变为求：
$$\{\begin{array}{l}\underset{\lambda }{\max }\underset{w,b}{\min }L(w,b,\lambda )\\ \\ s.t.{\lambda }_i\ge 0\end{array}$$
好了，现在问题先求解一个拉格朗日的最小值，可以用偏微分求解，得到一些条件。
即对
$$L(w,b,\lambda )=\frac{1}{2}{w}^{T}w+\sum _{i=1}^N{\lambda }_i(1-y_i(w{x}_i+b))$$
求关于参数的偏微分
$$\begin{gathered} \frac{\partial L(w,b,\lambda )}{\partial w}=w-\sum _{i=1}^N{\lambda }_i{y}_i{x}_i=0 \\ \Rightarrow w=\sum _{i=1}^N{\lambda }_i{y}_i{x}_i \end{gathered}$$
$$\begin{gathered} \frac{\partial L(w,b,\lambda )}{\partial b}=-\sum _{i=1}^N{\lambda }_i{y}_i=0 \\ \Rightarrow \sum _{i=1}^N{\lambda }_i{y}_i=0 \end{gathered}$$

有了这两个条件以后，原来的拉格朗日函数就可以进一步在最小值的条件中化简：
为了计算严谨，这里wx的点乘，表示为矩阵的转置乘法$w^{T}x$
$$\begin{gathered} L(w,b,\lambda )=\frac{1}{2}{w}^{T}w+\sum _{i=1}^N{\lambda }_i(1-y_i(w^T{x}_i+b)) \\ \Rightarrow minL(w,b,\lambda )=\frac{1}{2}{(\sum _{i=1}^N{\lambda }_i{y}_i{x}_i)}^T(\sum _{i=1}^N{\lambda }_i{y}_i{x}_i)+\sum _{i=1}^N{\lambda }_i-\sum _{i=1}^N{\lambda }_i{y}_i{w}^T{x}_i-\sum _{i=1}^{N}b{\lambda }_i{y}_i \\ \Rightarrow \frac{1}{2}{(\sum _{i=1}^N{\lambda }_i{y}_i{x}_i)}^T(\sum _{i=1}^N{\lambda }_i{y}_i{x}_i)+\sum _{i=1}^N{\lambda }_i-\sum _{i=1}^N{\lambda }_i{y}_i{w}^T{x}_i \\ \Rightarrow \frac{1}{2}(\sum _{i=1}^N\sum _{j=1}^N{\lambda }_i{\lambda }_j{y}_i{y}_j{x^T}_i{x}_j)+\sum _{i=1}^N{\lambda }_i-\sum _{i=1}^N{\lambda }_i{y}_i{w}^T{x}_i \\ \Rightarrow \frac{1}{2}(\sum _{i=1}^N\sum _{j=1}^N{\lambda }_i{\lambda }_j{y}_i{y}_j{x^T}_i{x}_j)+\sum _{i=1}^N{\lambda }_i-\sum _{i=1}^N{\lambda }_i{y}_i{(\sum _{j=1}^N{\lambda }_j{y}_j{x}_j)}^T{x}_i \\ \Rightarrow \frac{1}{2}(\sum _{i=1}^N\sum _{j=1}^N{\lambda }_i{\lambda }_j{y}_i{y}_j{x^T}_i{x}_j)+\sum _{i=1}^N{\lambda }_i-\sum _{i=1}^N\sum _{j=1}^N{\lambda }_i{y}_i{\lambda }_j{y}_j{x^T}_j{x}_i \\ \Rightarrow -\frac{1}{2}(\sum _{i=1}^N\sum _{j=1}^N{\lambda }_i{\lambda }_j{y}_i{y}_j{x^T}_i{x}_j)+\sum _{i=1}^N{\lambda }_i \end{gathered}$$
忙了半天我们现在可以更新我们的目标了：
$$\{\begin{array}{l}\underset{\lambda }{\max }-\frac{1}{2}({\sum }_{i=1}^N{\sum }_{j=1}^N{\lambda }_i{\lambda }_j{y}_i{y}_j{x^T}_i{x}_j)+{\sum }_{i=1}^N{\lambda }_i\\ s.t.\lambda \ge 0\end{array}$$
由KKT条件：

$$\{\begin{array}{l}\frac{\partial L}{\partial w}=0,\frac{\partial L}{\partial b}=0,\frac{\partial L}{\partial \lambda }=0\\ \\ {\lambda }_i(1-y_i(w{x}_i+b))=0\\ \\ 1-y_i(w{x}_i+b)\le 0\\ \\ {\lambda }_i\ge 0\end{array}$$
最终结果即将诞生：
(先推一下b，怕不知道b怎么来的)
$$\begin{gathered} 1-y_i(w{x}_i+b)=0 \\ {y}_i(w{x}_i+b)=1 \\ {y}_i^2(w{x}_i+b)=y_i \\ w{x}_i+b=y_i \\ b=y_i-w{x}_i \end{gathered}$$
最终结果：

$$\{\begin{array}{l}\begin{array}{l}\stackrel{\wedge }{w}={\sum }_{i=1}^N{\lambda }_i{y}_i{x}_i\\ \\ \stackrel{\wedge }{b}=y_k-x_k{\sum }_{i=1}^N{\lambda }_i{y}_i{x}_i\end{array}\end{array}$$
我们的决策函数即为：

$$h(x;w,b)=sign({\stackrel{\wedge }{w}}^{T}x+\stackrel{\wedge }{b})$$
这样我们的决策函数就出来了，关于后续的核函数和SMO方法 还有软间隔下一篇继续写，今天先写这么多。主要就是SVM的思想，优化办法，详细的推导过程与证明。
$$$$