凸优化

凸优化理论本身非常博大，事实上我也只是了解了一个皮毛中的皮毛，但是对于广大仅仅想要了解一下机器学习或者深度学习的同学来说，稍微了解一点凸优化也就够了。在实际工程问题中，比如现在我们用的最多的深度神经网络的求解优化问题，都是非凸的，因此很多凸优化理论中非常有价值的定理和方法，在非凸优化问题中不适用，或者说并没有收敛保证等。但是，作为知识的基础，依然有必要来理解和学习一下凸优化，本篇整理了非常基础的一些概念。主要参考网上一些资料，和《凸优化》这本书的一些概念。

凸优化理论基础中的基础

1. 为什么要学习凸优化？

凸优化在数学规划领域具有非常重要的地位。一旦将一个实际问题表述为凸优化问题，大体上意味着相应问题已经得到彻底解决，这是非凸的优化问题所不具有的性质。其应用非常广泛，机器学习中很多优化问题都要通过凸优化来求解；在非凸优化中，凸优化同样起到重要的作用，很多非凸优化问题，可以转化为凸优化问题来解决；

2. 什么是优化问题？ 

3. 什么是凸优化问题？ 

4. 什么是凸函数？ 

 
有一个经典的示意图：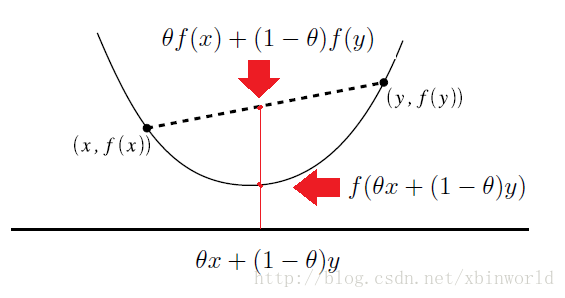 
 
凸函数的几何意义表示为函数任意两点的连线上的取值大于该点在函数上的取值

5. 凸函数的一阶充要条件 

一阶条件的意义是，对于函数在定义域的任意取值，函数的值都大于或者等于对函数在这点的一阶近似。用图来说明就是下图： 

口语化理解就是说凸函数总是在其任意一点的切线的上方（或者可以有部分相切的）。通过图可以很清楚地理解这个充要条件，但是，具体在应用中，我们不可能对每一个点都去计算函数的一阶导数，因此后面会说道利用凸函数的二阶特征来进行判断一个函数是否是一个凸函数。下面贴一下证明充分性和必要性的过程，来自《convex optimization》，不是很在意的同学可以跳过，直接看下一节。但是建议手推一下，还是比较简单的：

6. 凸函数的二阶充要条件 
记函数的一阶导数和二阶导数为g和H， 

其中要求函数ff二阶可微，则函数ff在定义域上式convex函数的充要条件是：函数的二阶导数（即Hessian矩阵）是半正定的，也就是所有的特征值都是大于等于0的。特殊的，对于一元函数，可以退化为f′′(x)≥0
--------------------- 
作者：大饼博士X 
来源：优快云 
原文：https://blog.youkuaiyun.com/xbinworld/article/details/79113218 
版权声明：本文为博主原创文章，转载请附上博文链接！