统计学习方法--笔记2

第二章  感知机

2.1感知机

感知机：二类线性分类模型，旨在求出将训练数据进行线性划分的分离超平面S

感知机属于判别模型：即直接求出条件概率

方法：导入基于误分类的损失函数，利用梯度下降法对损失模型进行最小化，求出模型
分类：原始模型和对偶模型

神经网络与支持向量机的基础

f(x)=sign(w*x+b)：感知机
w为权值向量，b为偏置(bias) sign()为符号函数，即x大于等于0,sign(x)=1，反之=-1

解释1：
    w*x+b=0是超平面S，其中w是S的法向量，b是S的截距，S被称为分离超平面，位于两部分的点分别被分为正、负两类。

2.2 学习策略
线性可分：存在某个S：w*x+b=0能偶将数据集完全正确划分，则称该数据集为线性可分数据集

为了确定w和b,需要确定一个学习策略，即定义 经验损失函数并将损失函数极小化

损失函数选择：
    1. 误分类点个数：不是连续可导函数，拒绝
    2. 误分类点到超平面距离：接受
        |w*x0+b|/|w|   其中|w|是 w的范数
   
    即：L(w,b)=-求和(y(w*x+b))   y是类的实际标签  

2.3 学习算法

M为误分类点的集合

感知机学习算法是误分类驱动，具体采用随机梯度下降法
先任意的选取超平面w0,b0，然后使用梯度下降法不断极小化目标函数 L(w,b)=-求和(y(w*x+b))

损失函数L(w,b)的梯度由

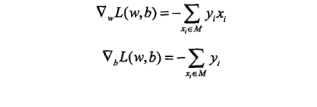
图1
给出，随机选取一个误分类点，对w,b进行更新：
w <- w+uyx
b <- b+uyx      //u是步长，又可以叫 学习率

原始形式：
    感知机的原始学习算法如图所示：

    图2
    理解：当一个实例点被误分类 ，即位于错误的一侧，则调整w,b的值，使超平面向该误分类点的一侧移动

感知机学习算法由于采用不同的初值或选取不同的误分类点，解可以不同

2.4 算法的收敛性：
将偏置b加入权重向量w中 w'=(w,b) ，同时，输入向量加以扩充补个1 x'=(x,1)
    w'*x'=w*x+b

定理1：Novikoff
    存在满足|w'|=1的超平面w'*x'=0将训练集完全正确分开，且存在s>0,使得y(w'*x')>=s
    令R=max|x'| ，则误分类次数k<=(R/s)^2

    

    说明误分类次数是有上界的，经过有限次搜索可以找到将训练数据完全正确分开的分离超平面S
   

    只要线性可分，感知机学习算法原始形式的迭代就是收敛的 
   

    当训练数据集线性不可分的时候，感知机算法不收敛，迭代结果会震荡

对偶形式：
    算法如图所示：

    图3
    对偶形式中训练实例仅以内积的形式出现，用矩阵的形式存储，即Gram矩阵