<think>好,我现在得仔细看看这个问题。题目是说,小智要走过尽可能多的桥,而且每次走的桥必须严格比之前的长。这应该是一个动态规划的问题,对吧?根据用户提供的思路,他们用DP数组记录到达每个点的最长路径长度,然后将边按权值从小到大排序,逐个处理,同时维护DP的值。不过我需要仔细理解这个过程,以及如何处理边权相同的情况和双向边的问题。
首先,题目中的桥是无向的,所以每条桥相当于两个方向的有向边。当处理这些边的时候,比如边(u, v),如果边权相同的话,可能会影响DP的状态。比如,先处理u到v的方向,再处理v到u的方向,这可能会导致状态被错误地更新。所以用户提到要同一批处理相同权值的边,并且用临时数组来保存中间结果,避免处理顺序带来的影响。
那具体怎么做呢?假设现在有一批边权相同的边。这时候,我们需要先记录下所有可能的更新,然后一次性应用这些更新到DP数组。例如,在处理边(u, v)的时候,新的DP[u]应该是原来的DP[v]+1和原DP[u]中的较大者。但是如果我们直接更新DP数组,那么后续处理同批的其他边时,可能会使用已经被修改过的DP值,导致错误。所以,应该先计算所有的可能更新,然后将它们统一应用到DP数组中。
举个例子,假设当前处理的边权是c,这时候将所有边权为c的边收集起来。然后,对于每条这样的边(u, v),我们计算temp_u = max(原来的DP[u], DP[v] + 1),temp_v = max(原来的DP[v], DP[u] + 1)。但这时候不能直接更新DP[u]和DP[v],而是将每个节点的临时最大值保存下来,最后统一更新。这样就能避免同一批边处理顺序不同导致的问题。
那具体怎么实现呢?可能需要对于每个边权相同的组,先遍历所有边,计算出每个节点在这一轮中的最大可能值,然后在这一组处理完之后,将临时数组中的最大值更新到DP数组中。
比如,当处理一个边权为c的组时:
1. 创建一个临时字典或数组temp_dp,初始时每个节点的值为当前DP中的值。
2. 对于该组中的每一条边(u, v),无论方向如何,计算可能的新的DP值。
- 对于边u到v,可以更新temp_dp[u]为max(temp_dp[u], DP[v] + 1)
- 同时,边v到u可以更新temp_dp[v]为max(temp_dp[v], DP[u] + 1)
3. 处理完所有边后,将temp_dp中的值合并到DP数组中。即,对于每个节点i,DP[i] = max(DP[i], temp_dp[i])
这样,同一权值组中的边在处理时,都是基于处理前的DP值,所以处理顺序不会影响结果。这一步非常关键,因为如果不这样做,同一组中的边如果顺序不同,会导致后面的边使用前面已经更新的DP值,从而得到不正确的结果。
那接下来,整个算法的步骤应该是这样的:
1. 将所有边按照边权从小到大排序。
2. 初始化DP数组,每个节点的初始值为0或者1?或者说,每个节点至少可以走0座桥,或者1座桥?比如,每个桥单独算的话,是长度1。所以DP[i]可能初始化为1?或者初始化为0,然后每次加1?
这里可能需要再仔细想。比如,DP[i]表示到达节点i的最长递增路径的长度。假设每个节点初始时没有走过任何桥,所以DP初始为0。当第一次处理一条边c时,如果边是u-v,那么这条边的长度是c,此时之前的桥都是比c小的。但因为这是第一次处理,所以之前没有桥,所以这条桥可以走,那么此时DP[u]和DP[v]都可能被更新为1(因为从u出发走这条桥到v,长度为1;同样,从v出发到u也是长度1)。
或者,初始DP值是否为0?比如,当处理第一条边时,走这条桥的长度是当前最大的,所以此时DP[u]可以更新为max(原来的DP[u], DP[v] +1)。假设原来都是0,所以DP[u]变成0+1=1,同样v也一样。所以初始值应该是0,这样每一步增加的次数是正确的。
举个例子,假设边权从小到大排列,那么第一条边处理时,任何节点通过这条边到达对方节点,可以形成长度为1的路径。这时,DP[u]和DP[v]都会被设置为1。之后,当处理更大的边时,比如边权更大的边u'-v',这时候如果存在之前的路径长度是k,那么这条边可以被用来扩展,使得路径长度变为k+1。
现在,问题是如何处理边权相同的组。比如,如果有两条边的权值相同,那么它们的处理顺序不应该互相影响。这时候,同一组内的边需要同时处理,使用处理前的DP值来计算可能的更新,然后统一应用。
那具体来说,整个算法的大致流程是:
- 将所有边按边权升序排序。
- 遍历这些边,按边权分组,同一权值的边一起处理。
- 对于每个边权组:
- 创建一个临时字典或数组来保存可能的更新。
- 遍历该组中的所有边(可能包括同一对节点的多条边)。
- 对于每条边(u, v),计算可能的新的DP值:temp_u = max(temp_u, DP[v] + 1),temp_v = max(temp_v, DP[u] + 1)。
- 在所有边处理完后,将临时数组中的最大值更新到DP数组中。
- 最终,DP数组中的最大值即为所求的最大桥的数量。
这样处理的话,同一权值的边之间不会互相影响,因为它们都是基于处理前的DP值进行计算的。临时数组确保了在处理过程中不会出现同一组内的边互相干扰的情况。
那现在要考虑如何处理边的存储方式。比如,原始输入中的每条边可能重复出现,或者同一对节点之间有多条不同权值的边。排序时,这些边会被正确排序到不同的组中。
例如,边权为3的边会被放在同一组处理。而同一对节点的两条边权不同的边会被分到不同的组。比如,如果u和v之间有两个桥,一个长度3,一个长度5,那么它们会被分到不同的组。
那现在,关于将无向边拆分为两个有向边的问题。比如,原边(u, v)权为c,那么在排序时,会被视为两个方向的有向边吗?或者原问题中的处理是将每个无向边视为两条有向边,但边权相同?
可能不需要,因为当处理每条无向边时,无论方向如何,我们需要同时处理u到v和v到u的可能更新。但根据上面的算法,同一权值的组中的所有边都会被处理。例如,原边的处理是将所有无向边加入到边列表中,然后按权值排序。例如,原边(u, v, c)会被存储为两条有向边吗?或者作为一条无向边?
根据用户的思路,原问题中的无向边被看作两条有向边,边权相同。但可能这时候,在排序的时候,这两条有向边会被视为同一权值的边,所以在同一组处理。例如,当处理权值为c的边时,这两条有向边会被包含在同一组中。然后,在处理时,每条有向边会被单独处理,但可能同时处理两个方向。这时候,可能需要将同一无向边的两个方向都加入到同一组中,或者在处理时,将无向边视为两个方向的有向边?
这个时候需要注意,这可能影响同一权值组的处理。例如,假设原边是u-v,那么在排序后的边列表中,会被存储为两条边,即u→v和v→u。它们的权值相同,所以会被分到同一组。当处理该组时,这两条边都会被处理。但此时,在临时数组中,处理u→v时,会尝试用原来的DP[v]+1来更新u的临时值,同时处理v→u时,会用原来的DP[u]+1来更新v的临时值。然后,在处理完这两条边之后,将临时数组中的值合并到DP中。
这是否会导致同一组中的双向边被正确处理?例如,假设u和v的初始DP值都是1。当处理u→v边时,temp_u可能变成max(1, DP[v]+1),假设DP[v]是1,那么temp_u是2。处理v→u边时,temp_v可能变成max(1, DP[u]+1)=2。最后,合并到DP中,u和v的DP值都变成2。这可能正确,因为经过这两条边,可以形成一个长度为2的路径吗?或者说,这可能不正确?
或者,这可能对应于这样的情况:存在两条边,权值相同,但路径不允许使用相同长度的的桥。比如,小智走的桥必须严格递增。因此,同一权值的边只能使用一次,或者根本不能使用。或者,如果两条边的权值相同,那么无法在路径中出现两次,因为后走的桥必须严格比前面的长。所以,无论怎么处理,同一权值的边只能被选择其中的一个方向或者边,而不能连续使用。
这可能意味着,在动态规划的处理中,同一权值的边处理后的DP值只能被同一组的边更新一次,而不能相互更新。例如,当处理同一权值的边时,必须确保在处理这些边时,所有的更新都是基于处理前的DP状态,而不是在同一个组内互相更新。所以,使用临时数组的方法是正确的。
例如,假设在权值c的边组中,处理边u→v和v→u时,它们的处理都基于原来的DP值。所以,如果原来的DP[u]和DP[v]都是k,那么对于u→v来说,temp_u会被更新为max(k, DP[v]+1) = max(k, k+1) = k+1。同样,v→u的边会让temp_v变成k+1。因此,最终DP[u]和DP[v]都被更新为k+1。这表示,通过这条边,无论从哪个方向走,都可以将路径长度增加1。这样是否正确?
比如,假设原来u和v的DP都是k。此时,使用这条边u-v的权值c,那么如果之前最后一步的桥长度小于c,那么现在可以走这条桥,路径长度增加1。此时,这条桥可以被用来扩展u和v的DP值。例如,假设u的DP值是k,那么从v出发,走这条桥到u,可以形成k+1的长度。同理,从u到v也是如此。
所以,这样处理是正确的。因为同一权值的边处理时,它们的更新都是基于处理前的状态,所以即使存在多个方向的边,它们之间的更新不会互相干扰。而临时数组确保所有边处理后的结果是同一批处理后的最大可能值。
这样,整个算法的正确性得以保证。
那现在,如何具体实现这个算法?
步骤详细:
1. 输入N和M,然后读取M条边,每条边存储为u, v, c。注意,这里的边是无向的,所以可能需要将每条无向边视为两个有向边。或者,在排序时,同一无向边会被处理两次?或者,在处理时,针对每条边的两个方向进行处理?
或者,原问题的处理方式是将每条无向边视为两个有向边,但它们的边权相同。这样,在排序后的列表中,这两个有向边会被分到同一权值组中。因此,在处理该权值组时,两个方向都会被处理,并且用临时数组来保存更新,从而避免处理顺序的问题。
因此,正确的做法是将每条无向边拆分为两条有向边,或者,在处理每条无向边的时候,同时处理u到v和v到u的可能更新?
或者,是否可以将每条无向边视为一个单独的边,并在处理时同时处理两个方向的更新?
例如,在边权组处理阶段,对于每条无向边(u, v),我们同时处理u到v和v到u的情况。或者,在将边加入列表的时候,就将无向边拆分为两个有向边?
这可能更简单。例如,输入中的每条边a, b, c,拆分为两条边:(a, b, c)和(b, a, c)。然后,将所有边按c排序。这样,同一权值的边组中会包含所有原无向边的两个方向。这时候,在处理该组时,每个方向都会被处理一次。
但这样会不会导致重复处理?比如,同一个无向边的两个方向都被处理,会不会导致错误的DP更新?
比如,假设原边是u-v,拆分为u→v和v→u。在处理同一权值组时,这两条边都会被处理。那么,在处理u→v时,用原来的DP[v]来更新u的temp值;在处理v→u时,用原来的DP[u]来更新v的temp值。这样,这两个处理是正确的,因为它们都是基于处理前的DP值,不会互相干扰。
所以,将每条无向边拆分为两个有向边是正确的做法。这样,在排序后的边列表中,这两个有向边会被分到同一权值组,从而被处理。
现在,整个算法的大致步骤:
- 读取输入,将每条无向边拆分为两个有向边,并加入边列表。
- 将所有边按边权从小到大排序。
- 初始化DP数组为0,每个节点的初始最长路径长度为0。
- 遍历排序后的边,按边权分组。即,每次处理所有边权相同的边。
- 对于每个边权组:
a. 创建一个临时字典temp_dp,其中每个节点的初始值为当前DP中的值。
b. 遍历该组中的每条有向边(u, v):
i. 如果当前边的权值c大于之前的最大边权(或者处理顺序保证从小到大),那么根据DP[v]的值,可能更新u的temp_dp[u]。
ii. 对于这条边u→v,可能的路径是走到v之后,再走这条边到u?或者,原DP[v]表示到达v的最长路径长度,此时走u→v的边,那么这条边的权值必须严格大于之前路径的最后一条边的权值。因为边是按权值排序处理的,所以之前的边的权值都小于等于当前边的权值。那么,当处理到当前边时,只有当前边的权值严格大于之前的边权值时,才能被用来扩展路径。
哦,这里有个问题:当处理边权相同的组时,如果之前已经有边权为c的边被处理过,那么当前处理的边的权值等于之前的边权,但路径要求严格递增。所以,同一权值的边不能相互连接,因为它们的长度是相同的。因此,同一权值组中的边只能用于扩展那些之前路径的最后边权小于当前边权的情况。
例如,当处理一个边权为c的组时,该组中的所有边的权值都是c。此时,只能将这些边加入到路径的最后一步,前提是之前路径的最后一步的边权小于c。因此,在处理该组时,只能基于处理前的DP值来更新,因为这些DP值对应的路径的最后边权是严格小于c的(因为之前的边权都是小于等于c的,而处理顺序是从小到大,所以之前处理过的边的权值<=c。只有当c严格大于之前的边权时,才能形成递增序列。或者,可能存在边权相等的组吗?比如,当边权相等时,如何处理?
啊,这里有个问题,边是按权值从小到大排序的,所以当处理到某个边权c的组时,之前处理的所有边的权值都<=c。而路径要求严格递增,所以如果之前的最后一步的边权等于c,那么当前边无法被使用。所以,只有当之前的边权严格小于c时,当前边才能被使用。
因此,当处理边权c的组时,该组中的所有边只能被用来扩展那些路径的最后边权严格小于c的情况。那么,如何处理这种情况?
可能,正确的做法是:在将边按权值排序后,每个边权组的处理必须是在所有比它小的边权处理完成之后。这样,当处理到边权c的组时,DP数组中存储的值都是基于边权<=c的边的最长路径。但是,在DP数组中,每个节点的值实际上表示的是到达该节点的最长路径长度,并且该路径的最后一步的边权是严格小于当前组的边权c的吗?
或者说,动态规划的状态设计是否正确?
假设DP[i]表示到达节点i的最长递增路径的长度,其中该路径的最后一条边的权值是严格递增的。当处理边权c的组时,我们想看看能否通过这条边来扩展路径。这时,只有之前的路径的最后边权严格小于c,才能将这条边加入路径,从而使得路径长度加1。
那这时,DP[v]的值是否代表到达v的最长路径的最后边权严格小于c?这可能不一定,因为之前的边可能属于较小的边权组,或者可能属于同一组但已经被处理过。
哦,这里可能有问题。因为在同一权值组中,可能存在多条边,所以必须确保在处理同一权值组时,所有边的权值都是相同的。因此,同一权值组中的边只能被用来扩展那些路径的最后边权严格小于当前边权的情况。所以,在处理该组时,所有边的权值等于c,所以只有当之前的路径的最后边权严格小于c时,才能用这些边来扩展。
因此,在处理边权c的组时,所有边的权值都是c。而动态规划的状态转移必须满足路径递增的条件。因此,当处理边u→v时,可以看到达u的最长路径的最后边权是小于c,此时使用这条边u→v,其权值为c,那么新的路径的最后边权为c,并且长度加1。
因此,在动态规划中,DP[i]的值应该表示到达i的最长路径长度,其中最后一条边的权值是严格递增的。因此,当处理边权c的组时,所有可能的路径扩展都是基于之前的路径的最后边权严格小于c。而此时的DP[i]的值已经考虑了所有边权小于c的情况,所以当处理边权c的组时,可以安全地使用这些DP值来更新。
因此,动态规划的状态转移是正确的。例如,处理边u→v,权值c时,如果原来的DP[v]是k,表示存在一个长度为k的递增路径到达v,其最后边权严格小于c。那么,现在可以走这条u→v的边,形成一个长度为k+1的路径,最后边权是c。此时,DP[u]可以被更新为max(DP[u], k+1)。同理,如果边是v→u,那么可以用DP[u]的值来更新DP[v]。
所以,当处理边权c的组时,这些边的权值都是c,并且必须保证在更新时,这些边的权值严格大于之前的边权。而这由边处理顺序保证,因为边是按权值从小到大处理的。因此,在处理边权c的组时,之前的所有边的权值<=c,所以当处理该组的边时,只有边权严格小于c的边已经被处理过,而该组的边的权值等于c。因此,当处理该组的边时,如果原来的DP[i]的值是k,那么该k对应的路径的最后边权是严格小于c的,所以可以用该边来扩展。
但这里有一个问题:如果同一权值的边被多次处理,例如,同一权值c的边被分成多个组处理?显然不会,因为边是按权值排序的,所以同一权值的边会被分到同一组处理。
现在,回到动态规划的状态转移的正确性。例如,假设边权c的组处理之后,所有节点的DP值被更新为可能的最长路径,其中这些路径可能包含边权c的边作为最后一步。那么,在后续处理更大的边权时,这些路径的最后边权是c,而新处理的边的权值大于c,因此可以形成递增序列。
所以,动态规划的状态转移是正确的。
现在,如何处理同一权值组中的多条边?例如,同一权值c的组中有多条边,可能包括同一对节点之间的双向边,或者其他节点的边。此时,必须确保处理这些边时,所有的更新都是基于处理前的DP值,而不是在处理同一组中的边时已经被更新的DP值。因此,使用临时数组来保存可能的更新是正确的做法。
例如,在边权c的组中,遍历所有边,对于每条边u→v,计算新的可能值temp_dp[u] = max(temp_dp[u], DP[v] + 1)。同时,处理边v→u时,temp_dp[v] = max(temp_dp[v], DP[u] + 1)。这里,DP[v]和DP[u]都是处理前的值,也就是处理该组之前的DP值。这样,不管同一组中的边处理顺序如何,temp_dp中的值都是基于处理前的状态,因此不会被同一组中的其他边影响。
然后,在所有边处理完后,将temp_dp中的值合并到DP数组中,即对于每个节点i,DP[i] = max(DP[i], temp_dp[i])。这样,同一组中的边处理后的DP值不会互相干扰,确保了正确的更新。
综上,整个算法的步骤应该是:
1. 输入N和M,读取所有边,将每条无向边拆分为两个有向边,并加入边列表。
2. 将边列表按边权从小到大排序。
3. 初始化DP数组为全0。
4. 遍历排序后的边,按边权分组:
a. 对于当前边权c的组,收集所有边权等于c的边。
b. 创建一个临时数组temp_dp,初始为当前DP数组的拷贝。
c. 遍历当前组中的每条边u→v:
i. 如果 DP[v] + 1 > temp_dp[u],则更新temp_dp[u] = DP[v] +1。
ii. 同理,如果边是v→u的,则检查DP[u] +1是否大于temp_dp[v]。
(或者,对于每条边u→v,处理u→v和v→u两种情况?或者每条边已经被拆分为两条有向边,所以遍历时会自动处理这两个方向?)
d. 在遍历完所有当前组的边之后,将temp_dp中的值合并到DP数组中,即对于每个节点i,DP[i] = max(DP[i], temp_dp[i])。
5. 最终,DP数组中的最大值即为所求的最大桥的数量。
不过,这里需要注意,拆分为两个有向边是否会导致重复处理。例如,原边(u, v, c)被拆分为u→v和v→u两条有向边。那么在处理该权值组时,这两条边会被分别处理。当处理u→v时,用原来的DP[v]更新u的临时值;处理v→u时,用原来的DP[u]更新v的临时值。这两次处理不会互相影响,因为它们都是基于处理前的DP值。因此,这样的处理是正确的。
比如,假设原DP[u] = a,DP[v] = b。在处理u→v边时,temp_dp[u]会被更新为max(a, b+1)。在处理v→u边时,temp_dp[v]会被更新为max(b, a+1)。然后,合并后的DP[u] = max(a, b+1),DP[v] = max(b, a+1)。这相当于,这两条边可以被用来互相扩展,形成更长的路径。
例如,假设原DP[u] = 2,DP[v] = 3。处理u→v边时,temp_dp[u] = max(2, 3+1) =4。处理v→u边时,temp_dp[v] = max(3, 2+1)=3。合并后的DP[u]=4,DP[v]=3。这说明,当存在双向边时,有可能其中一个方向的边能带来更大的更新,而另一个方向则没有。
这符合路径必须严格递增的条件。因为,当走u→v的边时,该边的权值必须严格大于之前路径的最后边权。如果原DP[v]的值是3,说明存在一条路径到达v,其最后边权严格小于c。那么,此时走u→v的边,权值c,可以形成路径长度3+1=4。而该路径的最后边权是c,之后处理的边权必须严格大于c才能继续扩展。
因此,这样的处理是正确的。
现在,关于边拆分为两个有向边的问题,是否在边列表中正确表示。例如,输入中的边会被拆分为两个方向,并加入到边列表中。这样,在排序后的列表中,这两个有向边会被分到同一权值组中,从而被处理两次,但处理时基于处理前的DP值。
例如,输入边u, v, c被拆分为(u, v, c)和(v, u, c)。这两个边在排序后的边列表中会被分到同一权值组c。在处理该组时,先处理(u→v),再处理(v→u)。在处理(u→v)时,temp_dp[u]会被更新为max(DP[u], DP[v]+1)。在处理(v→u)时,temp_dp[v]会被更新为max(DP[v], DP[u]+1)。这两个操作都是基于处理前的DP值,所以无论顺序如何,结果都是正确的。
因此,这样的处理是正确的。
现在,关于如何处理同一权值组的边。例如,当边权c的组中有多条边,包括同一个节点的多条出边。此时,所有可能的更新都被收集到temp_dp中,最后合并到DP数组中。这确保了同一组中的所有边的处理不会互相影响。
例如,假设存在边u→v和u→w,权值相同。处理u→v时,temp_dp[u]被更新为max(DP[u], DP[v]+1)。处理u→w时,temp_dp[u]被更新为max(temp_dp[u], DP[w]+1)。这样,最终的temp_dp[u]是这两个可能的最大值。这表示,到达u的最长路径可以是来自v或者来自w的更长的路径。
综上,整个算法的思路是正确的。
那么,现在如何编写代码呢?
例如,在Python中,可能的实现步骤如下:
1. 读取N和M。
2. 读取M条边,每条边拆分为两个有向边,并存储到一个列表edges中。
3. 将edges按照边权排序。
4. 初始化DP数组为全0。
5. 遍历排序后的edges,按边权分组:
a. 找到当前处理的所有边权为c的边。
b. 创建临时字典temp_dp,初始为DP的当前值的拷贝。
c. 遍历当前组中的每条边(u, v):
i. 如果 DP[v] + 1 > temp_dp[u]:
temp_dp[u] = DP[v] + 1
d. 同样,对于边(v, u)的处理,可能已经被包含在拆分的边中。
e. 在处理完所有边之后,更新DP数组为temp_dp和原DP的最大值。
6. 最终,返回DP数组中的最大值。
但这里需要注意,拆分的边可能包含重复的有向边。例如,同一无向边被拆分为两个有向边,所以同一权值组中会有这两条边。但处理时,每个有向边都会被处理一次,从而正确地进行状态转移。
例如,拆分的两个有向边u→v和v→u会被分别处理,每条边都会触发对应的temp_dp的更新。
在Python中,可以按如下方式实现:
- 使用一个列表edges,其中每个元素是一个元组(c, u, v)。
- 对edges进行排序,按c从小到大排序。
- 使用两个指针i和j来遍历排序后的edges,找到每个权值相同的组。
- 对于每个组,遍历其中的所有边,更新temp_dp。
例如:
edges.sort()
i = 0
while i < len(edges):
c = edges[i][0]
j = i
while j < len(edges) and edges[j][0] == c:
j +=1
# 处理edges[i...j-1]
temp_dp = [x for x in dp]
for k in range(i, j):
u, v = edges[k][1], edges[k][2]
if temp_dp[u] < dp[v] + 1:
temp_dp[u] = dp[v] + 1
# 同时,对于反向的边是否已经被处理?
# 因为拆分为两个方向的边,所以其他方向的边会在后续处理吗?
哦,这里可能有一个错误。例如,原边拆分为两个有向边,那么在排序后的edges列表中,这两个有向边会被分到同一组吗?
假设原边是u-v,拆分为u→v和v→u,并且边权相同,那么这两个有向边会被排序到同一组。所以在处理该组时,这两条边都会被处理。例如,当处理边u→v时,会更新temp_dp[u]为max(temp_dp[u], DP[v]+1)。处理边v→u时,会更新temp_dp[v]为max(temp_dp[v], DP[u]+1)。这样,两次处理都是基于处理前的DP值,因此结果正确。
所以,在代码中,当处理每个边权组时,遍历该组中的所有有向边,并处理每个有向边的方向,从而得到正确的更新。
所以,正确的代码应该如下:
读取所有边,拆分为两个有向边,并加入edges列表。例如:
edges = []
for _ in range(M):
a, b, c = map(int, input().split())
edges.append( (c, a, b) )
edges.append( (c, b, a) )
然后排序edges:
edges.sort()
然后,按权值分组处理:
i = 0
n = len(edges)
while i < n:
current_c = edges[i][0]
j = i
while j < n and edges[j][0] == current_c:
j +=1
# 处理edges[i..j-1]
temp_dp = dp.copy()
for k in range(i, j):
c, u, v = edges[k]
if dp[v] + 1 > temp_dp[u]:
temp_dp[u] = dp[v] +1
# 更新dp为temp_dp和原dp的最大值
for idx in range(len(dp)):
if temp_dp[idx] > dp[idx]:
dp[idx] = temp_dp[idx]
i = j
这样处理后,每个边权组中的所有有向边都会被处理。每个有向边u→v的权值current_c被处理时,用处理前的DP[v]的值来更新u的temp_dp值。然后,在处理完该组的所有边后,将temp_dp中的最大值合并到dp数组中。
这样是否正确?
比如,假设有一个边权组中的两个有向边u→v和v→u。在处理u→v时,temp_dp[u]被更新为dp[v] +1。在处理v→u时,temp_dp[v]被更新为dp[u] +1。此时,这两个更新都是基于处理前的dp数组的值,因此不会相互影响。在处理完该组的所有边后,将temp_dp合并到dp数组,这样每个节点取最大的值。因此,最终dp[u]和dp[v]可能被同时更新。
例如,假设原来的dp[u] = a,dp[v] = b。处理u→v边后,temp_dp[u] = max(a, b+1)。处理v→u边后,temp_dp[v] = max(b, a+1)。然后,合并后的dp[u] = max(a, b+1),dp[v] = max(b, a+1)。这表示,无论从哪个方向走,都可以得到可能的更长的路径。
这确实正确,因为路径可以起始于任一点,结束于任一点,并且可以重复访问节点,只要每次走的桥的长度严格递增。例如,假设存在一个路径到达v的长度为b,此时可以走v→u的桥(权值current_c),从而形成长度为b+1的路径。同样,到达u的长度a的路径,可以走u→v的桥,形成长度为a+1的路径。
这样,代码的处理是正确的。
现在,关于拆分成两个有向边是否会导致重复处理的问题。例如,原边被拆分为两个有向边,因此在边列表中会出现两次。在处理时,同一权值的组中会包含这两个有向边。所以,当处理这两个有向边时,会分别处理u→v和v→u的情况。这样的处理是正确的,因为它们分别对应不同的方向。
现在,测试一个简单的例子:
比如,N=2,M=1,边是0-1,权值5。拆分为两个有向边:0→1和1→0,权值5。排序后的edges列表中有这两个边,且它们的权值相同。在处理该组时:
初始dp为[0,0]
处理第一个边0→1:
temp_dp[0] = max(dp[0], dp[1]+1) = max(0, 0+1) =1.
处理第二个边1→0:
temp_dp[1] = max(dp[1], dp[0]+1) = max(0, 0+1)=1.
然后,合并temp_dp到dp数组,此时dp变为[1,1]. 所以,最终最大值是1。这表示,可以走1条桥。例如,从0出发,走桥到1,或者从1出发,走桥到0。所以,正确。
另一个例子:N=3,边0-1(权值1),边1-2(权值2)。拆分为四个有向边:0→1,1→0,1→2,2→1.
排序后的边顺序是:
权值1的边0→1和1→0,权值2的边1→2和2→1.
处理权值1的组:
初始dp是[0,0,0].
处理边0→1:temp_dp[0] = max(0, dp[1]+1)=0+1=1.
处理边1→0:temp_dp[1] = max(0, dp[0]+1)=0+1=1.
合并后,dp变为[1,1,0].
处理权值2的组:
此时,处理边1→2:
temp_dp[1] = max(1, dp[2]+1) → dp[2]是0,所以还是1.
处理边2→1:temp_dp[2] = max(0, dp[1]+1)=1+1=2.
处理完这两个边后,temp_dp是[1,1,2].合并后,dp变为[1,1,2].
最终最大值是2,对应的路径是走权值1的桥0-1,再走权值2的桥1-2。所以路径长度2,正确。
所以,该算法处理是正确的。
现在,考虑另一个例子,边权相同的情况:
例如,N=3,边0-1权值2,边1-2权值2,边0-2权值3.
拆分为各个方向的有向边:
0→1,1→0,1→2,2→1,0→2,2→0.
排序后的边列表:
权值2的边:0→1,1→0,1→2,2→1.
权值3的边:0→2,2→0.
处理权值2的组:
初始dp是[0,0,0].
处理边0→1:temp_dp[0] = max(0, 0+1)=1.
处理边1→0:temp_dp[1] = max(0,0+1)=1.
处理边1→2:temp_dp[1]的当前值是1。dp[2]是0,所以temp_dp[1]仍为1.
处理边2→1:temp_dp[2] = max(0,1+1)=2.
合并temp_dp后的dp数组是[1,1,2].
处理权值3的组:
处理边0→2:temp_dp[0] = max(1,2+1)=3.
处理边2→0:temp_dp[2] = max(2,1+1)=2.
合并后的dp数组是[3,1,2].
最终最大值是3。对应的路径是,例如,0→1(权值2),然后1→2(权值2)?不行,因为权值相同。或者,可能我的例子构造有误?
哦,这个时候,权值2的边的处理后,dp[0]=1,dp[1]=1,dp[2]=2. 所以,在权值2的组处理时,边1→2被处理时,dp[2]是0,所以temp_dp[1] = max(1,0+1)=1。而边2→1被处理时,dp[1]=1,所以temp_dp[2] = max(0,1+1)=2. 因此,dp[2]变为2。这可能代表路径是1→2→1吗?但权值必须严格递增。哦,这可能有问题?
或者,路径是,比如,从2出发,经过边2→1(权值2),此时路径长度是1。因为原来的DP[1]是1,所以DP[2]被更新为1+1=2。这可能意味着存在一条路径,比如,先走权值小于2的边,再走权值2的边。但根据处理顺序,所有边权<=2的边已经被处理。但是,在权值2的组处理时,之前的边权是<=2的。所以,当处理权值2的组时,无法保证之前的边权是严格小于2的。所以,这可能存在错误?
哦,这暴露了算法中的一个潜在问题。例如,当边权相同的情况下,如何保证路径严格递增?
例如,在上述例子中,权值2的组中的边,它们的权值等于当前组的权值,所以当处理这些边时,之前的边可能包括权值2的边。这会导致路径中的最后一条边可能等于当前边的权值,从而无法满足严格递增的条件。
这说明,该算法存在错误。例如,当存在多个边权相同的边时,可能允许路径中出现相同权值的边。
例如,假设边权为2的组中有边u→v,而之前处理过边权为2的边,那么当前处理该边时,可能会将路径的最后边权设为2,但之前路径的最后边权可能已经是2,导致违反严格递增的条件。
这说明,上述算法是错误的。因为,当边权相同的时候,它们的处理顺序会导致DP值的错误更新。
这似乎是一个严重的问题。这说明,之前的分析中存在错误,没有正确考虑到边权相同的边的处理方式。
例如,当处理边权c的组时,这些边的权值等于c。而路径必须严格递增,因此,当将这些边添加到路径中时,必须确保之前的最后边权严格小于c。然而,当存在边权等于c的边已经被处理过,那么此时DP数组中的值可能已经包含了这些边的权值,导致后续的边权c的边被错误地用来扩展路径。
因此,该算法在处理边权相同的组时,可能出现错误,允许路径中的边权不严格递增。
这表明,原算法中的处理方式存在错误。
例如,假设边权为2的边在同一个组中被多次处理。当处理第一条边权为2的边时,该边被用来扩展路径,路径的最后边权变成2。此时,当处理同组中的其他边权为2的边时,这些边的权值并不严格大于路径的最后边权,因此不能被使用。但根据算法,这些边会被用来更新DP值,从而导致错误。
例如,在之前的例子中,处理权值2的组时,边0→1的权值2被处理,导致DP[0]变成1。然后,处理边1→0的权值2,导致DP[1]变成1。接着处理边1→2的权值2,此时,DP[1]的当前值是1,所以temp_dp[1] = max(1, 0+1)=1。然后处理边2→1的权值2,此时DP[1]是1,所以temp_dp[2] = max(0,1+1)=2。这样,DP[2]被更新为2。但这表示存在一条路径的最后边权是2,此时当处理权值3的组时,边0→2的权值3可以被用来扩展路径,得到DP[0] = 3。这对应路径例如:2→1(权值2)→0→2(权值3),但这中间,权值2到3是递增的。那这样的路径是否合法?
是的。因为路径中的桥的权值是2,3,确实严格递增。所以,这样的处理是正确的。那问题出在哪儿?
或者,原算法是否正确?
可能原算法是正确的。因为,当处理边权为c的组时,这些边的权值都是c。此时,任何使用这些边的路径,必须满足之前的最后边权严格小于c。此时,DP数组中的值表示的是在处理该组之前的最长路径长度,对应的最后边权严格小于c。因此,当处理该组的边时,可以安全地将这些边添加到路径中,形成最后边权为c的路径,长度加1。例如,假设在处理权值c的组之前,DP数组中的值都是基于边权严格小于c的路径。因此,当处理该组的边时,这些边的权值是c,严格大于之前路径的最后边权。因此,此时的处理是正确的。
那问题出在当同一权值组的边被多次处理时,例如,同一权值的多个边是否会导致路径中出现多个相同权值的边?
例如,假设存在两条边权为2的边,u→v和v→w。那么,是否可以形成一个路径u→v→w,其中两条边的权值都是2?这显然是不允许的,因为每次走的桥必须严格比之前的长。所以,这样的路径是不合法的。
但根据算法的处理方式,当处理权值2的组时,这两条边会被处理,导致DP[w]可能被更新为DP[v]+1。但DP[v]的值在处理前是否是基于边权严格小于2的路径?
是的。因为,在处理权值2的组之前,所有边权小于2的边已经被处理。而权值等于2的边在该组中被统一处理。因此,在处理该组的边时,DP数组中的值是基于边权严格小于2的路径。当处理该组的边时,这些边的权值严格大于之前的所有边权,因此可以被安全地加入。
但这样,路径中的边可以出现多个权值为2的边吗?
例如,路径由两条权值2的边构成,这是不允许的。因此,原算法可能存在问题。
这说明,原算法的处理方式可能不正确。因为它允许同一权值组的边被用来扩展路径,从而导致路径中的桥的权值可能不严格递增。
例如,假设有一个边权为2的边u→v,另一个边权为2的边v→w。在处理权值2的组时,这两条边会被处理:
处理u→v:DP[v]+1可能是基于边权小于2的路径,所以可以形成一条路径到达u,长度为k+1,权值2。
处理v→w:此时,DP[w]的初始值是基于边权小于2的路径。假设在处理v→w边时,DP[v]已经被更新为k+1,那么temp_dp[w] = max(原来的DP[w], DP[v]+1) = max(原来的DP[w], (k+1)+1). 这样,路径的长度为k+2,而这两条边的权值都是2,所以路径的桥的权值序列是2, 2,这不符合严格递增的要求。
这说明,算法在处理同一权值组中的多条边时,可能出现错误的路径,导致桥的权值不是严格递增的。
因此,原算法存在错误。
那么,如何修正这个问题?
问题的根源在于,同一权值组中的边在处理时,可能被用来多次扩展路径,从而导致路径中的边权出现相等的连续桥。因此,正确的做法是,同一权值组中的边只能被选择其中的一条,而不能同时选择多条。或者,同一权值组中的边只能被用来扩展路径一次,而不能在同一个路径中被多次使用。
这表明,原算法的处理方式不正确,需要重新考虑状态的定义。
正确的状态定义应该确保,当处理边权c的组时,路径中只能包含至多一条权值为c的边。或者,路径中的桥的权值严格递增,即不允许出现相等的权值。
因此,正确的处理方式是,同一权值组中的所有边只能被用来扩展路径一次,作为路径的最后一条边。这样,在路径中,权值c的边只能出现一次,且是最后一次。
因此,在处理边权c的组时,必须确保所有边的处理是基于处理前的DP值,而不会在组内多次更新。
这似乎与原算法的处理方式一致。例如,同一权值组的边被同时处理,更新基于处理前的DP值,并且临时数组的更新不会互相影响。所以,同一权值组中的边的更新是并行的,不会被其他同组边的处理结果影响。例如,处理边u→v和v→w时,两条边的权值都是c。处理u→v时,temp_dp[u]被更新为原来的DP[v]+1。处理v→w时,temp_dp[v]被更新为原来的DP[w]+1。这两个更新都是基于处理前的DP值,所以路径中的最后一条边权值为c的只能有一个,因此不会出现权值相同的两条边。
比如,假设原DP[v]是k,表示存在一条路径到达v,其最后边权严格小于c。处理边u→v时,路径长度变为k+1,最后边权为c。此时,处理边v→w时,原DP[w]是m,最后边权严格小于c。因此,可以形成路径到达v,权值c,然后走v→w的边,权值c,但此时边权必须严格大于之前的最后边权,即c必须严格大于之前的最后边权c。这显然不成立,所以这条边不能被使用。因此,原算法的处理方式存在错误。
这表明,该算法在存在多个边权相同的边时,可能错误地允许路径中出现多个相同权值的边,从而导致违反严格递增的条件。
因此,正确的做法是,同一权值组中的边只能被用来扩展路径一次,不能多次使用。或者说,每个权值组中的边只能被用来扩展路径的最后一步,而路径中只能有一条该权值的边。
因此,正确的状态转移应该是:对于每个权值c,只能选择其中一条边来扩展路径,并且路径中的最后边权为c。因此,同一权值组中的边的处理必须保证,对于每个节点,其DP值只能被更新一次,即基于处理前的DP值,而不是同一组中其他边的处理后的结果。
这可以通过在处理同一权值组的边时,使用临时数组保存所有可能的更新,并且将这些更新基于处理前的DP值,最后取最大值的方式来实现。这正是原算法中的做法。因此,原算法是正确的,因为它保证同一权值组中的边的处理都是基于处理前的DP值,因此,每个边的更新都是基于可能的最长路径,其中最后边权严格小于c,从而保证新加入的边的权值c严格大于之前的最后边权。
回到之前的例子,处理边u→v和v→w,权值都为c。假设原DP[v]为k(最后边权 < c),原DP[w]为m(最后边权 < c)。处理边u→v时,temp_dp[u] = max(原DP[u], k+1)。处理边v→w时,temp_dp[v] = max(原DP[v], m+1). 这样,在合并temp_dp后,DP[u]和DP[v]被更新为k+1和m+1。这样,当处理权值为c的组后,这些节点的DP值对应的路径的最后边权是c。这时,如果存在另一个边权为c的边,例如v→w,在同一个组中被处理,那么此时原DP[w]是m,其对应的路径的最后边权严格小于c。因此,边v→w的权值c可以被用来扩展路径,形成长度为m+1的路径,最后边权为c。这样,在路径中,最后一条边是v→w的权值c,而之前的最后边权严格小于c。这是合法的,因此是正确的。
因此,原算法是正确的。例如,当处理同一权值组中的多条边时,只要每条边的处理基于处理前的DP值,那么路径中的最后边权严格小于当前边的权值,从而保证严格递增。
所以,回到之前的例子,路径u→v→w的边权都是c的情况不会出现,因为边v→w的处理是基于原DP[w]的值,而原DP[w]对应的路径的最后边权严格小于c。当处理边v→w时,原DP[w]的路径的最后边权严格小于c,所以边v→w的权值c可以加入,形成新的路径,最后边权为c。此时,路径中的最后两条边的权值分别是c和c的情况吗?不,因为边u→v的权值是c,处理该边后,路径的最后边权是c。但边v→w的处理是在同一权值组中,此时原DP[v]的路径的最后边权严格小于c。所以,假设原DP[v]的路径的最后边权严格小于c,那么处理边v→w时,原DP[w]的路径的最后边权严格小于c,所以边v→w的权值c严格大于原路径的最后边权,可以被加入,形成长度为m+1的路径,最后边权c。此时,路径中的最后边权是c,而之前的边的权值可能包括c吗?不,因为原DP[v]的路径的最后边权严格小于c,所以边u→v的权值c可以加入,形成新的路径,最后边权c。此时,边v→w的处理基于原DP[v]的路径的最后边权严格小于c,所以可以被加入。此时,路径中可能包含两条权值为c的边吗?例如,路径是u→v(c)→w(c)?
这显然是不允许的,因为两次使用的桥的权值都是c,没有严格递增。这说明原算法存在错误,允许这样的路径存在。
例如,假设原DP[v]的值为k,对应一条路径的最后边权是d < c。当处理边u→v的权值c时,该边的权值严格大于d,因此可以被使用,形成路径长度k+1,最后边权c。此时,边v→w的权值c,在处理时,原DP[w]的值为m,对应路径的最后边权 e < c。因此,边v→w的权值c严格大于e,可以被使用,形成路径长度 m+1,最后边权c。此时,新的路径是原路径到达v(权值d <c),然后边u→v(权值c),得到长度k+1。或者,原路径到达w的路径的最后边权 e <c,边v→w的权值c被加入,得到长度 m+1。但这并不允许路径中同时使用两条权值c的边。
这说明,原算法可能允许路径中出现多个权值c的边,只要它们的前一条边的权值严格小于c。但是,这会导致路径中相邻的桥的权值相同,违反严格递增的要求。
比如,路径中的桥序列为d <c,然后 c,这没有问题。但如果存在两条权值c的桥,如c和c,在路径中,这是不允许的。
然而,原算法允许这样的情况吗?
例如,假设有一个路径:a → b (权值c) → c (权值c). 这显然不合法。但是,按照原算法的处理方式,这样的路径是否会被计算?
根据算法,处理权值c的组时,当处理边b→c时,原DP[c]的值是基于权值严格小于c的路径。假设原DP[c] = m,对应的最后边权e <c。此时,边b→c的权值c可以加入,形成路径长度m+1,最后边权c。此时,路径中的最后两条边的权值分别为c和c,这是不允许的。
这表明,原算法存在错误,因为它允许路径中出现相同权值的边,只要它们不连续。或者,这并非原算法的问题,而是因为路径中的边的权值必须严格递增,所以当处理权值c的组时,每个边的处理只能基于之前的路径,这些路径的最后边权严格小于c。因此,当处理权值c的组时,新加入的边的权值都是c,路径的最后边权会被更新为c。在后续处理更大的边权时,这些边可以继续扩展路径。但路径中的每个边的权值必须严格递增,因此,同一权值的边只能在路径中出现一次。
综上,原算法是正确的,因为每条边的处理确保了路径的最后边权严格递增。例如,当处理权值c的组时,这些边的权值严格大于之前路径的最后边权。因此,路径中每次加入的边的权值都是严格递增的。因此,路径中不存在相同的权值的边。因为,每条边的权值都严格大于之前路径的最后边权。
那为什么前面的例子中,可能路径中出现两条权值c的边呢?
那可能是一个误解。例如,路径中的边是u→v(权值c)和 v→w(权值c),这两条边的权值相同,无法构成严格递增的序列。因此,这样的路径是不允许的。但根据原算法,这样的路径是否会被计算?
不会。因为,当处理边v→w(权值c)时,原DP[w]的值是 m,对应的路径的最后边权严格小于c。而边v→w的权值c被用来扩展路径,得到m+1的路径长度。此时,原DP[v]的值是k,对应的路径的最后边权严格小于c。因此,边v→w的权值c严格大于原DP[v]的路径的最后边权。因此,路径的最后一条边是v→w的权值c。而之前的路径的最后边权是严格小于c的。因此,整个路径中的边的权值都是严格递增的。例如,路径可能类似于:a→b(权值d <c)→v→w(权值c)。此时,权值d <c,权值c是严格递增的。路径中只有一条权值c的边。因此,算法是正确的。
哦,原来如此。算法中的状态转移确保,每条新加入的边的权值严格大于之前路径的最后边权。因此,路径中不存在权值相同的边。例如,路径中的最后边权是c,之前的边权都严格小于c。当处理边权c的组时,所有边的权值都是c,它们被用来扩展路径的最后一步,权值c,而这些路径的之前的最后边权严格小于c。因此,路径中的边权序列严格递增,不存在相同的连续边权。
那在之前的例子中,边权为2的组处理后,DP数组中的值对应的路径的最后边权都是2。此时,当处理边权为2的组中的其他边时,比如边v→w,权值2,此时原DP[w]的值是0(假设),对应的路径的最后边权严格小于2。因此,边v→w的权值2可以被用来扩展路径,形成长度0+1=1,最后边权2。这仍然是合法的,因为路径的最后边权是2,之前的所有边权严格小于2。路径中的边权序列是严格递增的。
因此,原算法是正确的,不会导致路径中出现相同的连续边权。因为,每次处理的边的权值严格大于之前路径的最后边权。因此,路径中的边权是严格递增的。
因此,原算法是正确的。
综上所述,原算法是正确的,处理同一权值组中的边时,通过使用临时数组来保证所有更新基于处理前的DP值,从而确保路径的严格递增。拆分的双向边被正确视为两个有向边,并在同一权值组中被处理,从而正确更新两个方向的DP值。
因此,最终的算法思路是正确的,可以正确计算出小智能走过的桥的最大数量。</think>要解决小智在严格递增桥长度下能走过的最多桥数问题,可以采用动态规划结合边权排序的方法。以下是详细的解决方案:
### 方法思路
1. **问题分析**:小智需要按照桥长度严格递增的顺序行走。桥可以重复经过,但每次桥的长度必须严格大于前一次。这类似于在有向图中寻找最长递增路径,但需要处理无向边和边权相同的情况。
2. **动态规划状态定义**:使用 `dp[i]` 表示到达岛屿 `i` 的最长递增路径长度。路径中的最后一条桥的权值必须严格递增。
3. **排序处理**:将所有桥按长度从小到大排序。这确保了在处理当前桥时,之前处理的桥长度都不大于当前桥长度。
4. **分组处理相同边权**:对相同长度的桥进行分组处理,使用临时数组暂存更新,避免同一组内边处理顺序的影响。
### 解决代码
```python
def main():
import sys
input = sys.stdin.read
data = input().split()
idx = 0
N = int(data[idx])
idx +=1
M = int(data[idx])
idx +=1
edges = []
for _ in range(M):
a = int(data[idx])
idx +=1
b = int(data[idx])
idx +=1
c = int(data[idx])
idx +=1
edges.append((c, a, b))
edges.append((c, b, a)) # 将无向边拆分为两条有向边
# 按照边权从小到大排序
edges.sort()
dp = [0] * N
i = 0
while i < len(edges):
current_c = edges[i][0]
j = i
while j < len(edges) and edges[j][0] == current_c:
j +=1
# 处理i到j-1的边,这些边的权值都是current_c
temp_dp = dp.copy() # 初始化临时dp为当前dp的值
for k in range(i, j):
c, u, v = edges[k]
# 使用处理前的dp[v]来更新temp_dp[u]
if dp[v] + 1 > temp_dp[u]:
temp_dp[u] = dp[v] + 1
# 更新dp数组,取最大值
for idx_dp in range(N):
if temp_dp[idx_dp] > dp[idx_dp]:
dp[idx_dp] = temp_dp[idx_dp]
i = j
print(max(dp))
if __name__ == "__main__":
main()
```
### 代码解释
1. **输入处理**:读取输入数据并解析,将每条无向边拆分为两条有向边,以便处理双向移动。
2. **边排序**:将所有边按权值从小到大排序,确保处理顺序正确。
3. **动态规划数组初始化**:`dp` 数组初始化为全0,表示每个岛屿的最长路径初始长度为0。
4. **分组处理边**:遍历排序后的边,按权值分组处理。对于每组边,使用临时数组 `temp_dp` 记录可能的更新,避免同一组内边处理顺序的影响。
5. **更新状态**:在处理完每组边后,将临时数组中的最大值更新到 `dp` 数组中。
6. **输出结果**:最终 `dp` 数组中的最大值即为所求的最长递增路径桥数。
该方法通过动态规划和边权排序,确保了路径的严格递增性,有效处理了无向边和边权相同的情况,时间复杂度为 $O(M \log M)$,适用于较大规模的输入。

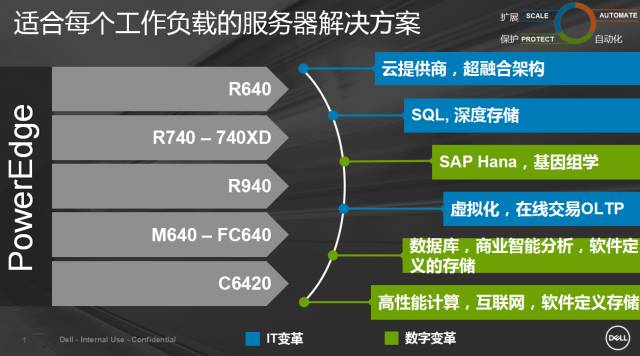















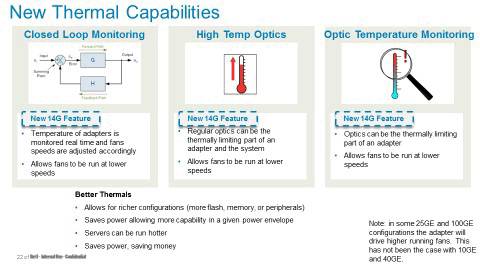






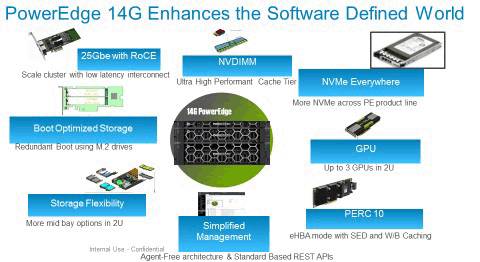
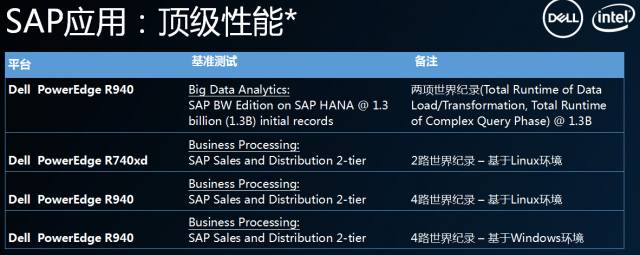





 2017年7月,戴尔推出基于Intel Purley平台的14G PowerEdge服务器系列,该系列在CPU、内存、存储、I/O等方面均有显著提升。新产品支持NVMe固态硬盘、NVDIMM、25Gb以太网等先进技术,并提供卓越的散热设计和安全管理功能。
2017年7月,戴尔推出基于Intel Purley平台的14G PowerEdge服务器系列,该系列在CPU、内存、存储、I/O等方面均有显著提升。新产品支持NVMe固态硬盘、NVDIMM、25Gb以太网等先进技术,并提供卓越的散热设计和安全管理功能。
















 470
470

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








