FC成环器内部真的是个环么

FC成环器内部真的是个环么

       我们知道在FC流行的时代，控制器与硬盘之间的连接方式是FC-AL仲裁环。环上的所有节点手拉手连接起来，将数据在这个大环上传递，每个节点根据数据包的FCAL地址来判断是不是给自己，的是就收下，不是就继续往外扔，直到某个节点认领。

         然而，如果盘数一增多，那么手拉手接力传数据的方式显然效率是很低的。而且FCAL环有个毛病就是必须按照一个方向传递，同时它还是个同步环，也就是环上同一时刻只有两个节点之间在互传数据，其他节点只起到接力的作用。这显然效率也很低，理论上完全可以做到环内任意两个点之间可以同时并行传输数据。但是FC协议刚出现的时候，那时候瓶颈其实还不在于FC传递上，而在于FC网络节点的性能自身。比如机械硬盘平均处理每个IO耗费10ms，而FCAL环路就算绕一大圈也不过几百微秒的时延，相比机械硬盘的慢速响应而言微不足道。但是随着FCAL环接入硬盘数量的不断增加，系统需要同时将指令发送给多个硬盘并行处理，并发请求数量上来之后，FCAL的同步特性就严重制约了并发度。

         于是人们就在想能否让数据一条直达。当FC协议在传统存储系统中得到大量普及之后，业界做FC成环器的厂商比如当时的PMC-Sierra公司，就发明了一种直接交换而不用大家手拉手接力传递的成环芯片，其内部其实是个Crossbar交换电路了，只不过依然需要遵循FCAL的协议，也就是先仲裁，后传数据。

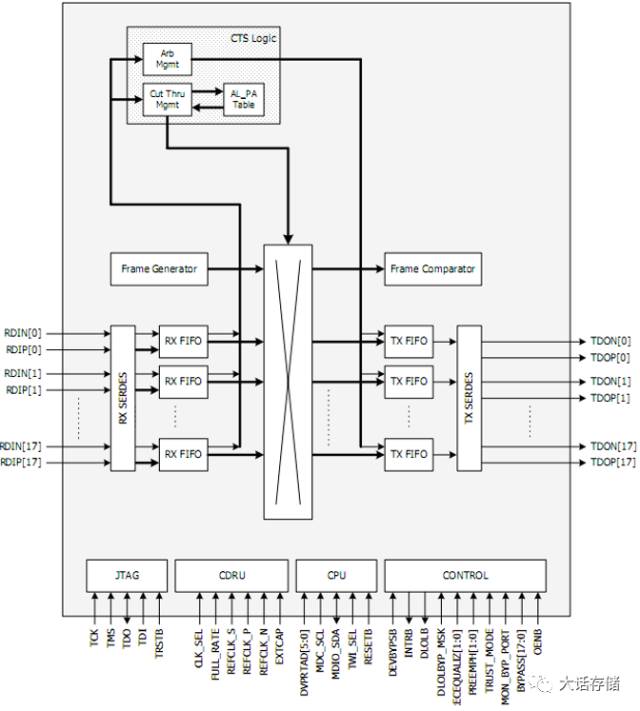
         其内部的固件负责接收仲裁广播，并直接独立裁决，也就是不将这笔广播发送到FC环路上真的让大家参与仲裁，因为这样会非常慢。裁决模块会均衡的让所有人都有机会获得仲裁胜利。仲裁模块会直接返回仲裁成功结果给发起端，降低了时延，于是发起端直接开始传送数据，发起端节点并不知道该数据是怎么传递到目的的，它认为底层还是大家帮忙接力传过去的。而实际上，是由成环器芯片通过Crossbar电路直接交换到对端的。利用这种方式，既能保持对上层协议的不修改、对节点固件的不修改，还能够提升性能。