Common Subsequence POJ（最长公共子序列+动态规划）

题意
题意非常的明显及求给定两个序列的最长公共子序列，值得一提的是这个题目是求最长公共子序列，并不要求所求得的序列连续(求最长公共子串是要求连续的，不知道大家什么感觉反正菜鸡的我经常把这个两个问题搞混)；
题目连接：原题连接
解析
最长公共子序列问题一般都是用动态规划来解题，当然动态规划的用途有很多，这只是其中之一。
动态规划的解题关键就是寻找子问题，把大问题分解成子问题，可以通过子问题的结果进而来得到大问题的结果，说白了就是自底向上的求解问题的过程。
首先我们将两个字符串分别设为"a0,a1…,an"以及"b0,b1,…bm",c[i][j]用来储存到ai以及bj时的最长公共子序列，对于这一个问题，我们可以分解为两种情况：
1.当ai==bj时，这时可知c[i][j]=c[i-1][j-1]。
2.当ai!=bj时，这时的c[i][j]易得即为max(c[i-1][j],c[i][j-1])。
附上公式即为：

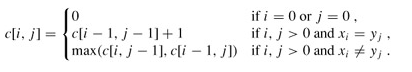
代码

#include<stdio.h>
#include<string.h>
char s1[505],s2[505];
int dp[505][505];
int max(int a,int b)
{
    return a>b?a:b;
}
int main()
{
    while(scanf("%s%s",s1,s2)!=EOF)
    {
        memset(dp,0,sizeof(dp));
        int len1=strlen(s1);
        int len2=strlen(s2);
        for(int i=1;i<=len1;i++)
        {
            for(int j=1;j<=len2;j++)
            {
                if(s1[i-1]==s2[j-1])
                {
                    dp[i][j]=dp[i-1][j-1]+1;
                }
                else
                {
                    dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
                }
            }
        }
        printf("%d\n",dp[len1][len2]);
    }
    return 0;
}

若有不妥，欢迎指正。