【c/c++】机试中的动态规划问题

动态规划问题(DP).

1. 递推求解问题

题目描述：

N 阶楼梯上楼问题：一次可以走两阶或一阶，问有多少种上楼方式。（要求采用非递归）

输入：

输入包括一个整数 N,(1<=N<90)。

输出：

可能有多组测试数据，对于每组数据，输出当楼梯阶数是 N 时的上楼方式个数。

样例输入：

4

样例输出： 

5

解题思路，当只有1层阶梯时只有1种上楼方式，2层阶梯时有2中上楼方式，当有n层阶梯时，则为 F(n-1)，即从n-1层直接到达，或者是从n-2层直接到达，故 F[n] = F[n-1] + F[n-2],代码为：

#include<stdio.h>
//结果可能非常大
long long F[91];
int main()
{
	int N;
	F[1] = 1;
	F[2] = 2;
	for (int i = 3; i <= 90; i++)
		F[i] = F[i - 1] + F[i - 2];
	while (scanf("%d", &N) != EOF)
	{
		printf("%lld\n", F[N]);
	}
	return 0;
}

 2. 错排公式问题

 假设有n个信封，求n个信全部装错信封的情况。问题的思路是当只有1个信时，F[1] = 0, 当有2个信时，F[2] = 1，当有 n 个信时，分2种情况：1是n-1个信装错了信封，第n个信没有装错，则将第n个信封中的信n装到前 n - 1个信封中的任意一个即可，共有n-1中选择，则这种方式共有 (n - 1) * F[n - 1]种情况；2是n-2个信封全部装错，第n-1和第n-2个信封装对，则调换第 n - 1和第 n 个信封中的信即可，第n-1个信封有 n -1 中选择，所以共有 (n -1)*F[n - 2]种情况。

如果上面的描述比较难以理解的话，可以理解为：第n个信封装了信k，第m个信封装了信n，若果k 不为m，调换过两个信封后，有n - 1个信封全部装错，又因为 m 是不为n的信封，共有n-1种选择，所以用 (n - 1) * F[n - 1]种情况；当k为m，调换后共有n - 2个信封装错，同样m有 n - 1种选择，所以用 (n -1)*F[n - 2]种情况，F[n] = (n - 1) * F[n - 1] + (n - 1) * F[n - 2];

代码为：

#include<cstdio>
using namespace std;
long long F[21];

int main()
{
    F[1] = 0;
    F[2] = 1;
    for(int i = 3; i <= 20; i++)
        F[i] = (i - 1) * F[i - 1] + (i - 1) * F[i - 2];
    int n;
    while(scanf("%d", &n) != EOF)
        printf("%d\n", F[n]);
    return 0;
}

运行结果：

3. 最长递增子序列问题：

给定一个序列，序列本身是无序的，要求从这个序列中找出一个最长的子序列，该子序列递增。

思想是，当只有1个元素时，F[1] = 1; 当有多个元素时，每个元素 ai ，F[i]表示以ai为结尾的递增子序列的长度，如果ai 在原序列中所有 j < i,都有 aj >= ai， 则F[i] = 1, 如果 存在 j < i， 又有 aj < ai, 那么结果是 所有 F[j] + 1中最大的那个值作为 F[i]。

同理当要求得一个非递增子序列的最长长度，同样可以使用这种方法，只需求 所有 满足 j < i,有aj >= ai的F[j] + 1中的最大值作为F[i]即可，最后遍历所有的F[i]找到最大的那个即为最长非递增子序列。

非递增子序列的代码为：

#include<cstdio>
#include<algorithm>
//包含了max函数，可以处理整数与浮点数
//max(x, max(y,z))可以得到三个数中的最大值
using namespace std;
int list[26];
int dp[26];

int main()
{
    int n;
    while(scanf("%d", &n) != EOF)
    {
        for(int i = 1; i <= n; i++)
            scanf("%d", &list[i]);
        for(int i = 1; i <= n; i++)
        {
            int tmax = 1;
            for(int j = 1; j <= i; j++)
            {
                if(list[j] >= list[i])
                {
                    tmax = max(tmax, dp[j] + 1);
                }
            }
            dp[i] = tmax;
        }
        int ans = 1;
        for(int i = 1; i <= n; i++)
            ans = max(ans, dp[i]);
        printf("%d\n", ans);
        sort(dp + 1, dp + n + 1);
        printf("sort后得到的结果: %d\n", dp[n]);
    }
    return 0;
}

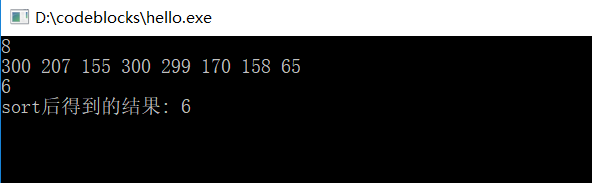
运行结果为：

4. 最长公共子序列问题

给出2个字符串，要求给出它们最长的公共子序列，子序列不一定是连续的，思路是dp[i][0] = dp[0][j] = 0，0表示一个字符串的前0个字符，而对于S1的第 i 个字符，S2的第 j个字符，若 S[i - 1] == s[j - 1]，则dp[i][j] = dp[i - 1][j - 1] + 1，不相同时有dp[i][j] = max(dp[i-1][j], dp[i][j-1])，因为dp[i][j]之前的dp都是已知的。

代码为：

#include<cstdio>
#include<string.h>
#include<algorithm>
//包含了max函数，可以处理整数与浮点数
//max(x, max(y,z))可以得到三个数中的最大值
using namespace std;
int dp[101][101];

int main()
{
    char S1[101], S2[101];
    while(scanf("%s%s", S1, S2) != EOF)
    {
        int L1 = strlen(S1);
        int L2 = strlen(S2);
        //注意字符串的下标应该从1开始，0表示长度为0，S1[0]的值应该以下标为1来表示
        //dp中的下标表示的是用来比较的两个子串的长度
        for(int i = 1; i <= L1; i++)
            dp[i][0] = 0;
        for(int i = 1; i <= L2; i++)
            dp[0][i] = 0;
        for(int i = 1; i <= L1; i++)
        {
            for(int j = 1; j <= L2; j++)
            {
                if(S1[i - 1] != S2[j - 1])
                {
                    dp[i][j] = max(dp[i][j - 1], dp[i - 1][j]);
                }
                else
                    dp[i][j] = dp[i - 1][j - 1] + 1;
            }
        }
        printf("%d\n", dp[L1][L2]);
    }
    return 0;
}

运行结果：

5. 最长回文子串问题

对于回文问题，可以设置两个端点 i 和 j ，分别从字符串的开始与末尾推进，判断当前子串是否是回文的，回文串逆序后与原字符串顺序相同，可以i不动，j从后推进到字符串首，然后i再推进一步，j再从串尾推进到串首。

当然为了简便起见，这里使用动态规划的方法实现，dp[i][j]为0时表示下标从i到j的子串不为回文串，为1时表示为回文串,

边界 dp[i][i] = 1, dp[i][i+1] = 1(S[i] = S[i+1])，或者dp[i][j] = dp[i + 1][ j - 1]，S[i] == S[j]时成立; 否则为0.

最难的部分是 i 和 j 的推进顺序，因为dp[i][j]要依赖于dp[i+1][j - 1]，而这个数可能还没有出来。

解决办法是对长度为3一直到总长的子串进行遍历，这样可以保证上面的问题不会发生。

代码为：

#include<cstdio>
#include<string.h>
#include<algorithm>
//包含了max函数，可以处理整数与浮点数
//max(x, max(y,z))可以得到三个数中的最大值
using namespace std;
int dp[101][101];

int main()
{
    char S[101];
    gets(S);
    int len = strlen(S);
    int ans = 1;//回文子串的长度最小为1，因为一个字符就是一个回文子串
    memset(dp, 0, sizeof(dp));
    //设定边界
    for(int i = 0; i < len; i++)
    {
        dp[i][i] = 1;
        if(i < len - 1)
        {
            if(S[i] == S[i+1])
            {
                dp[i][i+1] = 1;
                ans = 2;
            }
        }
    }
    for(int L = 3; L <= len; L++)
    {
        for(int i = 0;i + L - 1 < len; i++)//每次推进1步
        {
            int j = i + L - 1;//判别当前子串的右端点
            if(S[i] == S[j] && dp[i + 1][j - 1] == 1)
            {
                dp[i][j] = 1;
                ans = L;
            }
        }
    }
    printf("%d\n", ans);
    return 0;
}

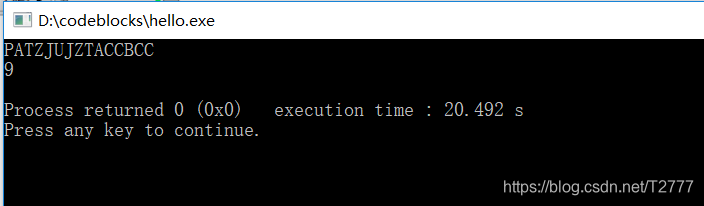
运行结果(ATZJUJZTA)：

6. 背包问题

0-1背包问题：

对于0-1背包问题，背包容量为s，现在有n种物品，每种物品只有1个，物品的体积为w，价值为v，要求求得最大背包能放物品的价值。

暴力的方法就是枚举进行，当然这种方法不太现实，用动态规划的方法考虑，dp[i][j]表示体积不超过 j 时，前 i 个物品所能达到的最大价值，此时不一定 i 个物品全都放入背包，但是是遍历到所给出的前 i 个物品用容量为 j 的背包所能得到的最大价值，j <= s,此时dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - list[i].w] +list[i].v)，即根据两者的最大值选择放入第 i 个物品或者选择不放入第 i 个物品，以此将所有的dp[i][j]求得，并根据dp[i - 1]求得dp[i]的各个值，注意代码中要对容量进行限制：

代码为：

#include<cstdio>
#include<string.h>
#include<algorithm>
//包含了max函数，可以处理整数与浮点数
//max(x, max(y,z))可以得到三个数中的最大值
using namespace std;
int dp[101][101];
struct E{
    int w;
    int v;
}list[101];

int main()
{
    int s, n;//s表示背包的总重量，n表示共有多少物品
    while(scanf("%d%d", &s, &n) != EOF)
    {
        for(int i = 1; i <= n; i++)
            scanf("%d%d", &list[i].w, &list[i].v);
        for(int i = 0;i <= s; i++)
            dp[0][i] = 0;
        for(int i = 1; i <= n; i++)
        {
            for(int j = s; j >= list[i].w; j--)
            {
                dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - list[i].w] + list[i].v);//根据条件选择加入背包或者不加入
            }
            for(int j = list[i].w - 1; j >= 0; j--)
                dp[i][j] = dp[i - 1][j];//不能加入背包
        }
        printf("%d\n", dp[n][s]);
    }
    return 0;
}

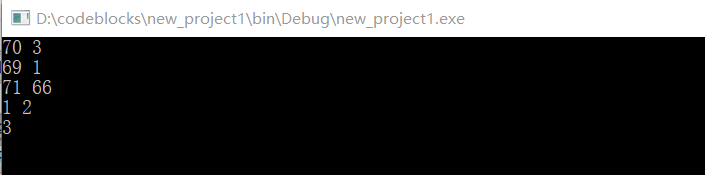
运行结果：

对于0-1背包问题可以将二维数组转变为一维的情况，需要注意的是上面的j的遍历从前往后或从后往前都不影响，但是一维的情况，dp[i][j] = max(dp[i-1][j], dp[i -1][j - list[i].w] + list[i].v)给出了是由i-1推导出的，但是用一维的情况时，由于不再记录i-1,而是对dp[j]进行更新，dp[j-list[i].w]（是上次i-1遍历时的结果）必须在不被更改的情况下对dp[j]实现修改，而dp[j-list[i].w]则需要在后面进行修改，它的更改不依赖于比自己下标大的。

用一维实现的代码：

#include<cstdio>
#include<string.h>
#include<algorithm>
//包含了max函数，可以处理整数与浮点数
//max(x, max(y,z))可以得到三个数中的最大值
using namespace std;
int dp[101];
struct E{
    int w;
    int v;
}list[101];

int main()
{
    int s, n;//s表示背包的总重量，n表示共有多少物品
    while(scanf("%d%d", &s, &n) != EOF)
    {
        for(int i = 1; i <= n; i++)
            scanf("%d%d", &list[i].w, &list[i].v);
        for(int i = 0;i <= s; i++)
            dp[i] = 0;
        for(int i = 1; i <= n; i++)
        {
            //j < list[i].w时，dp[j] = dp[j]不做修改
            for(int j = s; j >= list[i].w; j--)
            {
                dp[j] = max(dp[j], dp[j - list[i].w] + list[i].v); //括号里的dp[j]实际是dp[i-1][j]
            }
        }
        printf("%d\n", dp[s]);
    }
    return 0;
}

运行结果：

完全背包问题：

完全背包问题中，每种物品可以有无穷多个，题目为：背包重量为s,要求恰好装到s，共有n种物品，求最小的价值：

恰好要做的改变 dp[0] = 0, 其它的 dp[i] = 无穷大即不存在 dp[0][i](i > 0) 这种0个物品恰好重量为 i 的情况，只要满足了这个边界条件，就能使得恰好成立。最小的价值只要将max改为min即可，正因为有恰好这个条件，所以才能求 min。

完全背包的遍历要从小到大，即从 list[i].w到 s，因为每种物品可以有多个，dp[i][j] = min(dp[i-1][j], dp[i][j - list[i].w] + list[i].v),所以大的dp[j]要根据小的dp[j]来确定。

代码为：

#include<cstdio>
#include<string.h>
#include<algorithm>
#define INF 0x3fffffff
//包含了max函数，可以处理整数与浮点数
//max(x, max(y,z))可以得到三个数中的最大值
using namespace std;
int dp[101];
struct E{
    int w;
    int v;
}list[101];

int main()
{
    int T;
    scanf("%d", &T);
    while(T--)
    {
        int s, tmp;
        scanf("%d%d", &tmp, &s);
        s -= tmp;
        int n;
        scanf("%d", &n);
        //i表示前i种物品，所以下标从1开始
        for(int i = 1; i <= n; i++)
            scanf("%d%d", &list[i].v, &list[i].w);//注意输入顺序
        for(int i = 0; i <= s; i++)
            dp[i] = INF;
        dp[0] = 0;
        for(int i = 1; i <= n; i++)
            for(int j = list[i].w; j <= s; j++)
            {
                if(dp[j - list[i].w] != INF)
                {
                    dp[j] = min(dp[j], dp[j - list[i].w] + list[i].v);
                }
            }
        if(dp[s] != INF)
            printf("%d\n", dp[s]);

    }
    return 0;
}

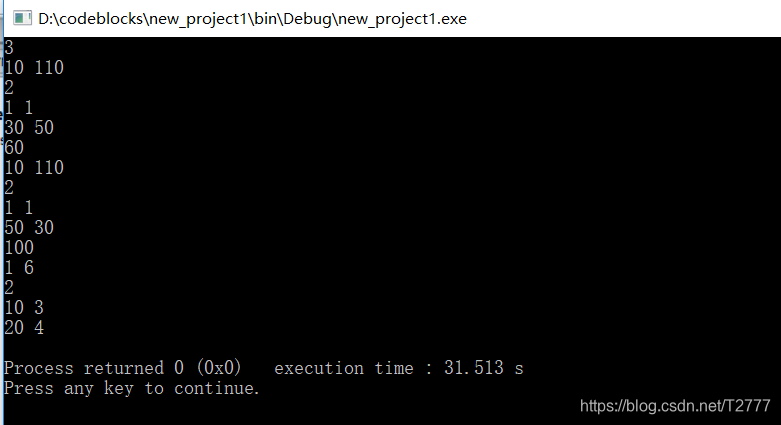
运行结果：

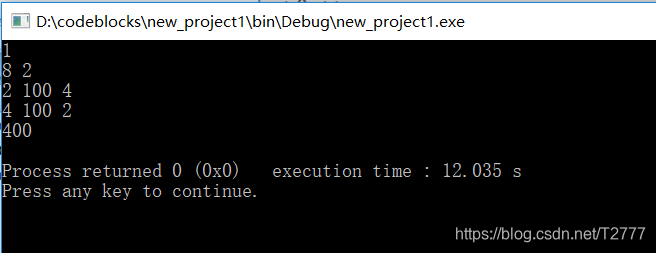
多重背包问题：

多重背包问题的思想是每种物品的数量不再是一种或者是无穷，而给出确定的数目，解决办法是转换为0-1背包问题，即将同一种物品看做不同的物品，将它们按照 0 - 1背包问题去解决。为了进一步的优化，对于第 i 种物品有 k 件，我们将它按照 1 件 2件，4件。。。直到 k - 2^c + 1（最后剩余的不够幂的）件进行分组，每一组成为一个新的物品，这样因为价值最大的取法，要么取1件，要么取2件，3,。。。都能用 1 搭配取到1,2,3,4,5...，所以按照这种思想可以大大降低复杂度。剩下的按照0-1背包问题解决即可，不同的分组，都视为 1 种新的物品，所以 n 将要更新为新的cnt。

大米代码为：

#include<cstdio>
#include<string.h>
#include<algorithm>
#define INF 0x3fffffff
//包含了max函数，可以处理整数与浮点数
//max(x, max(y,z))可以得到三个数中的最大值
using namespace std;
int dp[101];
struct E{
    int w;//价格成为重量
    int v;//重量成为价值
}list[101];

int main()
{
    int T;
    scanf("%d", &T);
    while(T--)
    {
        int s, n;
        int cnt = 0;
        scanf("%d%d", &s, &n);
        for(int i = 1; i <= n; i++)
        {
             int v, w, k;
             scanf("%d%d%d", &w, &v, &k);
             int c = 1;
             while(k - c > 0)
             {
                 k -= c;
                 list[++cnt].w = c * w;
                 list[cnt].v = c * v;
                 c *= 2;
             }
             list[++cnt].w = w * k;
             list[cnt].v = v * k;
        }
        for(int i = 0; i <= s; i++)
            dp[i] = 0;
        for(int i = 1; i <= cnt; i++)
            for(int j = s; j >= list[i].w; j--)
            {
                dp[j] = max(dp[j], dp[j - list[i].w] + list[i].v);
            }
        printf("%d\n", dp[s]);
    }
    return 0;
}

运行结果：