蓝桥杯 剪邮票 A组 C++

剪邮票

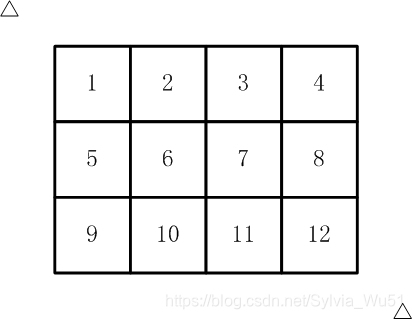
如【图1.jpg】, 有12张连在一起的12生肖的邮票。
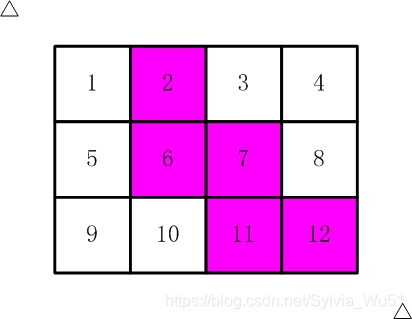
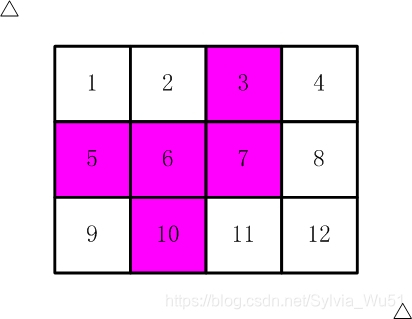
现在你要从中剪下5张来，要求必须是连着的。（仅仅连接一个角不算相连）比如，【图2.jpg】，【图3.jpg】中，粉红色所示部分就是合格的剪取。

请你计算，一共有多少种不同的剪取方法。

请填写表示方案数目的整数。
注意：你提交的应该是一个整数，不要填写任何多余的内容或说明性文字。



方法一：

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
int a[12]={0,0,0,0,0,0,0,1,1,1,1,1};
int map[3][4];

void dfs(int x,int y,int mapp[3][4]){
	mapp[x][y]=0;
	if(x-1>=0&&mapp[x-1][y]==1)  dfs( x - 1, y,mapp);
	if(x+1<3&&mapp[x+1][y]==1)  dfs(x + 1, y,mapp);
	if(y-1>=0&&mapp[x][y-1]==1)  dfs( x, y - 1,mapp);
	if(y+1<4&&mapp[x][y+1]==1)  dfs(x, y + 1,mapp);
	
} 
bool check(int a[12]){
	memset(map,0,sizeof(map));
	for(int i=0;i<3;i++){             //将一维坐标转为二维坐标 
		for(int j=0;j<4;j++){
			if(a[i*4+j]==1){
				map[i][j]=1;
			}
		}
	}
	int count=0; //记录连通数 
	for(int i=0;i<3;i++){             //判断连通性 
		for(int j=0;j<4;j++){
			if(map[i][j]==1){  //如果找到一个标记为1的点，则用深度搜索将这个点周围的点标记为0  
				dfs(i,j,map);  //如果所有点是连通的count=1； 
				count++; 
			}
		}
	}
	if(count!=1){
		return false;
	}
	return true;
} 
int main(){
	int ans=0;
	do{            //对数组a进行全排列，1表示选中 
		if(check(a)){ //检查是否连通 
			ans++;
		}
		
	}while(next_permutation(a,a+12));
	cout<<ans;
	return 0;
} 

方法二：
(转自：https://blog.youkuaiyun.com/u014552756/article/details/50946197)
思路：先找到5个数的组合，然后从第一个数字开始遍历，经过上下左右操作检测5个数是否都被访问一遍，如果5个数都可以遍历到则种类+1。

在原图中向上为-4，向下为+4，向左为-1，向右为+1，但是遇到3 4 5 7 8这种4+1=5但是这种情况不符合，所以重构一下原图：

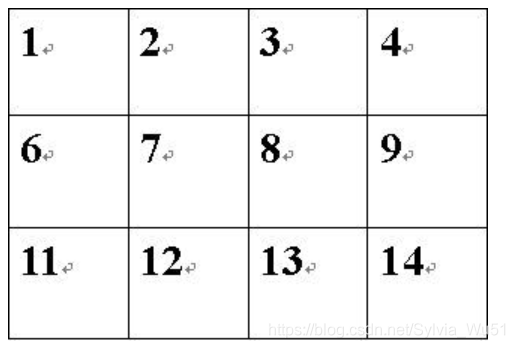
这样，向上为-5，向下为+5，向左为-1，向右为+1，避免了每行最后一个+1后等于下一行第一个的情况。

答案：116

#include <iostream>
using namespace std;
int mp[12]= {1,2,3,4,6,7,8,9,11,12,13,14};  
int aa[5],vis[5],sum=0;  //aa[5]用来存储当前选中的5个数   
int b[4]= {-1,1,-5,+5};
void dfs(int n)
{
    for(int i=0; i<4; i++)
    {
        int t=aa[n]+b[i];    //计算这个数相邻的点的数值 
        if(t<1||t>14||t==5||t==10) continue; 
        for(int j=0; j<5; j++)      //判断剩下的四个数字中是否有和这个数相邻的点的相等数值 
            if(!vis[j]&&aa[j]==t)   //若相等说明有相邻的数 
            {
                vis[j]=1;    //将这个相邻的点标记为访问过 
                dfs(j);    //访问这个相邻点的相邻点 
            }
    }
}
 
int main()
{
 
    for(int a=0; a<12; a++)
        for(int b=a+1; b<12; b++)
            for(int c=b+1; c<12; c++)
                for(int d=c+1; d<12; d++)
                    for(int e=d+1; e<12; e++)
                    {
                        aa[0]=mp[a];
                        aa[1]=mp[b];
                        aa[2]=mp[c];
                        aa[3]=mp[d];
                        aa[4]=mp[e];
                        for(int i=0; i<5; i++)   //初始化数组vis[n]; 
                            vis[i]=0;
                        vis[0]=1;  //aa[0]标记已访问  
                        dfs(0);  
                        int flag=1;
                        for(int i=0; i<5; i++)   //若每个点都能被标记访问过说明这5个点是连通的 
                        {
                            if(vis[i]!=1)    //如果有一个不为1说明其中有点不连通 
                            {
                                flag=0;
                                break;
                            }
                        }
                        if(flag==0) continue;  
                        else
                            sum++;
                    }
 
    cout<<sum<<endl;
 
    return 0;
}