n的阶乘中尾随零的个数（了解到大数操作）

计算n(1<=n<=1000)的阶乘有多少个尾随零。

阶段1：

思路：

• 刚开始做这道题的时候，我是先求出n！再计算有多少个0
  这样的复杂度很大，而且当n逐渐增大，int甚至long都存储不下n的阶乘的值。了解到可以使用BigInteger类型来存放阶乘值（暂未深入了解，先不展开说）。

• n!可以质因数分解，由于2*5=10，所以尾零的个数只与2和5有关
  一组2,5说明尾零个数+1，但是能被2整除的频率比被5整除的频率高的多，所以尾零的个数其实只和5相关，
  n！能被多少个5整除，就有多少个0

阶段2（循环）：

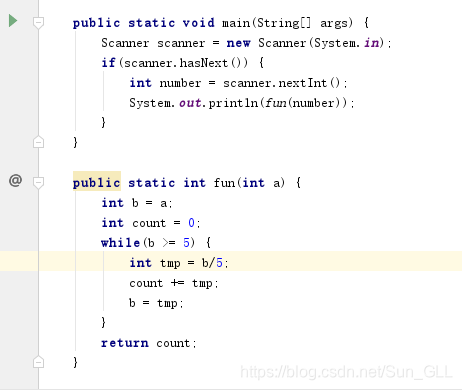
阶段三（递归）：