排序算法---归并排序（JAVA）

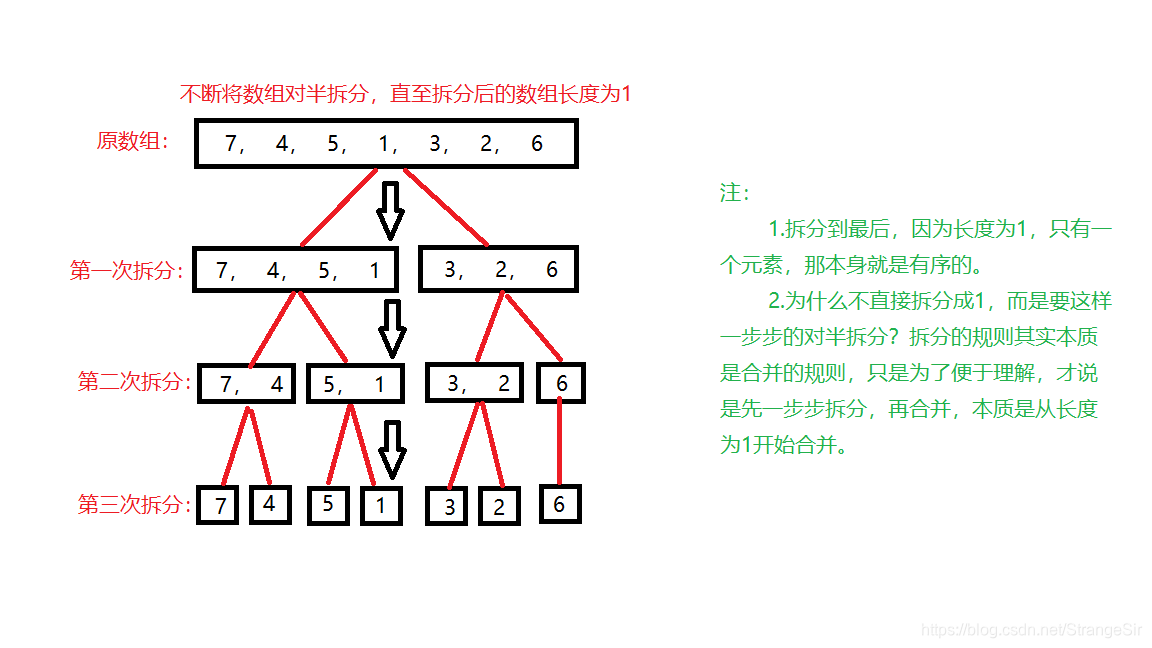
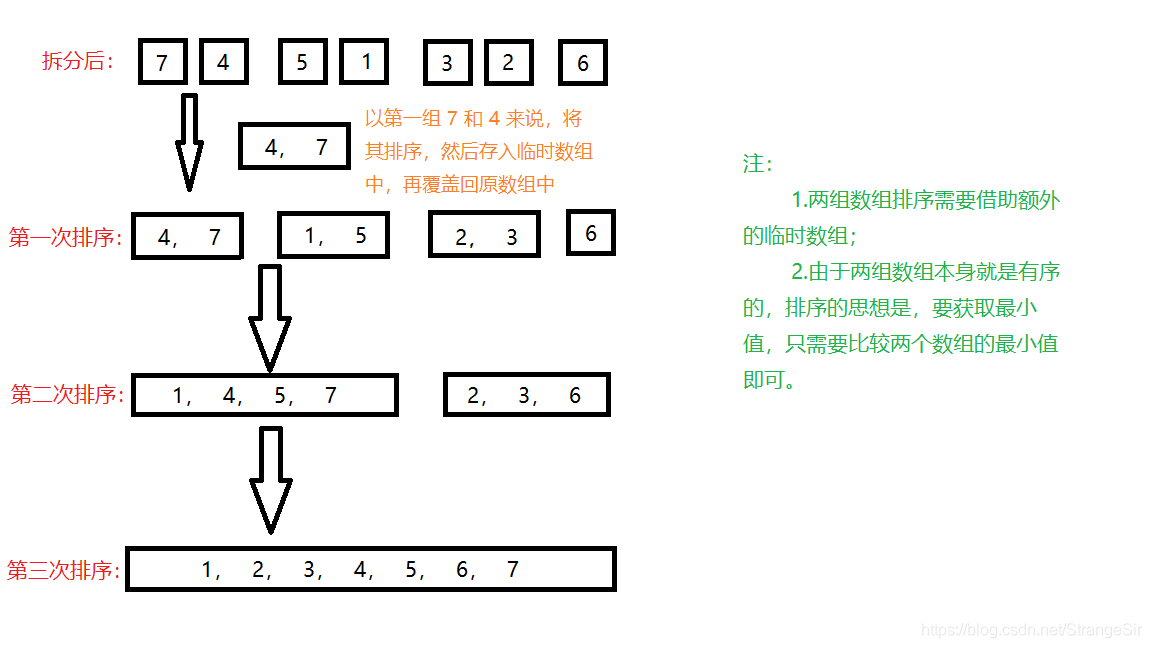
思路

代码

// 归并排序
public static void mergeSort(Integer[] arr) {
	mergeSort(arr, new int[arr.length], 0, arr.length-1);
}

// 归并排序
private static void mergeSort(Integer[] arr, int[] temp, int start, int end) {
	if (start < end) {
		int mid = (start + end) / 2;
		mergeSort(arr, temp, start, mid);
		mergeSort(arr, temp, mid + 1, end);
		merge(arr, temp, start, mid, end);
	}
}

/**
 * 归并排序，合并两个数组
 * @param arr 原数组
 * @param temp 临时数组
 * @param start 准备排序的左边数组的起始索引
 * @param mid 准备排序的左边数组的结束索引
 * @param end 准备排序的右边数组的结束索引
 */
private static void merge(Integer[] arr, int[] temp, int start, int mid, int end) {
	if (start >= end) {
		return;
	}
	int start1 = start;
	int end1 = mid;
	int start2 = mid + 1;
	int end2 = end;
	int len = end2 - start1 + 1;
	// 将两段数组合并排序到临时数组中
	for (int i = 0; i < len; i++) {
		if (start1 > end1) {
			temp[i] = arr[start2++];
			continue;
		}
		if (start2 > end2) {
			temp[i] = arr[start1++];
			continue;
		}
		if (arr[start1] < arr[start2]) {
			temp[i] = arr[start1++];
		} else {
			temp[i] = arr[start2++];
		}
	}
	// 将临时数组的数据覆盖回原数组
	for (int i = start; i <= end; i++) {
		arr[i] = temp[i-start];
	}
}

总结

归并排序体现了一种分治的思想，将数组的排序拆分成若干个长度为1的数组的组合排序，再将组合好的继续组合。这同样用到了递归，在数组长度较大时，要注意堆栈溢出的问题，解决思路同样是在拆分到一定大小时，选择使用其它的排序方式，减少递归次数。