台湾大学林轩田《机器学习基石》学习笔记第13讲——Hazard of Overfitting

上一节课中，我们介绍了通过non-linear feature transform把non-linear问题转化到linear问题进行学习，带来的代价是model complexity的增加。这节课我们将来看看complexity的增加带来的overfitting的问题。

一、What is Overfitting?

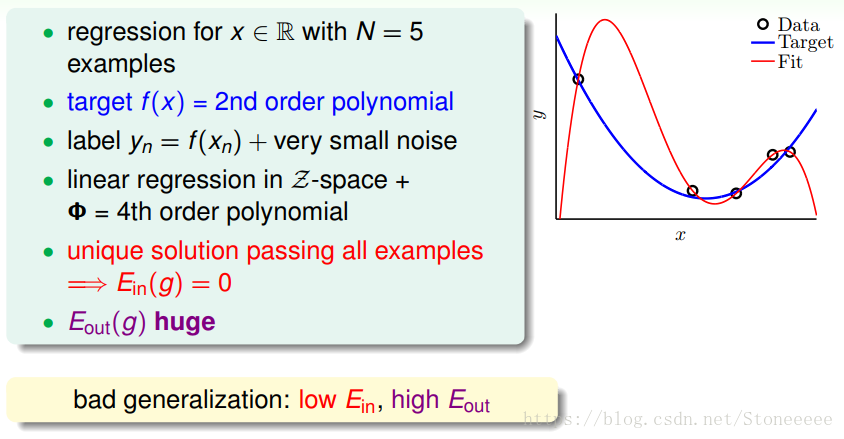
• 首先，看这样一个例子，红色线使用了更高阶的函数来进行学习，虽然所有的训练data都正确，即Ein(g)=0，但Eout(g)却很大，因此我们说这样的算法bad generalization泛化能力差。
  
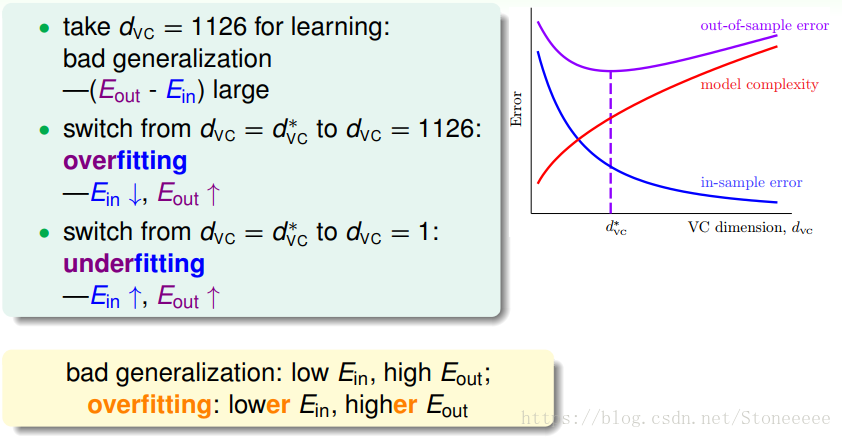
• 机器学习的目标结果是希望Eout很小，但有两种情况可能导致Eout变大：
• overfitting：Ein↓ Eout↑
• underfitting：Ein↑ Eout↑
  
• 导致overfitting的因素可能有：
• $d_{VC}$
• noise
• limited data size N

二、The Role of Noise and Data Size

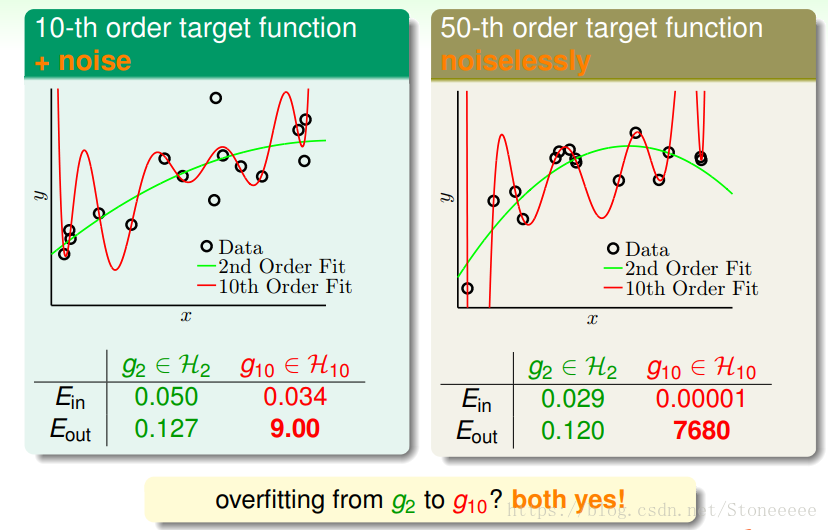
• 考虑这样的两个case：
• 第一个case中的training data包含noise，同时已知其目标函数是10阶的；第二个case中的training data不包含noise，同时已知其目标函数是50阶的；然后分别用2阶和10阶的模型去做fitting；
• 结果10阶模型都发生了过拟合，反而2阶的模型却表现得相对不错。这好像违背了我们的第一感觉，比如对于目标函数是10阶多项式，加上noise的模型，按道理来说应该是10阶的模型更能接近于目标函数，因为它们阶数相同。但是，事实却是2阶模型泛化能力更强；
• 这种现象产生的原因，从哲学上来说，就是“以退为进”。有时候，简单的学习模型反而能表现的更好。

首先回顾一下第9节中学到learning curve：

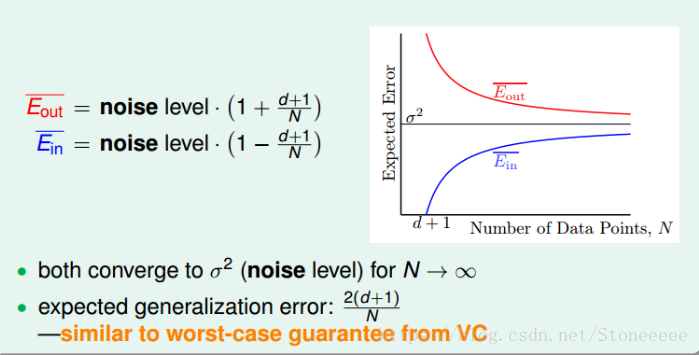
以下分别是2阶和10阶的learning curve：

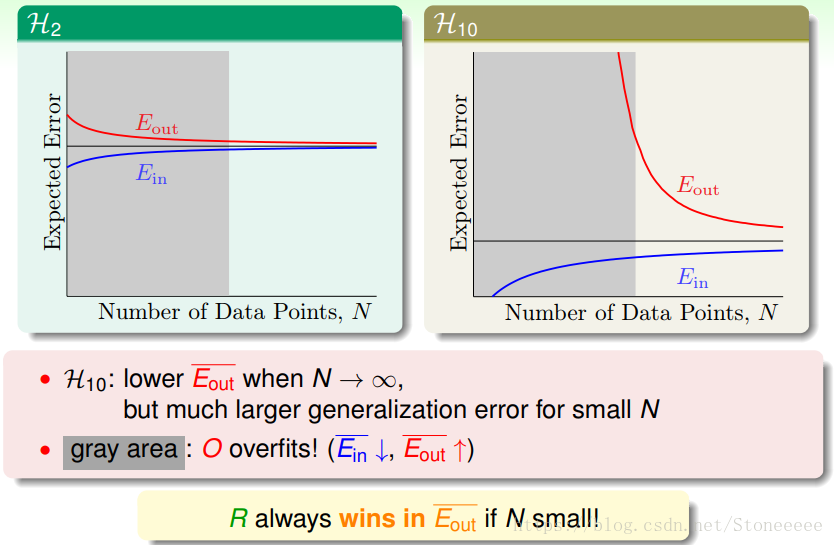
• 对于10阶的模型，只有在N很大的时候，才能获得小的Eout；
• 而对于2阶的模型，在N比较小的时候就能获得比较小的Eout，即在N小的时候，2阶模型具有较好的泛化能力；
• 值得一提的是，如果数据量N很大的时候，上面两图中Ein和Eout都比较接近，但是对于高阶模型，z域中的特征很多的时候，需要的样本数量N很大，且容易发生维度灾难。

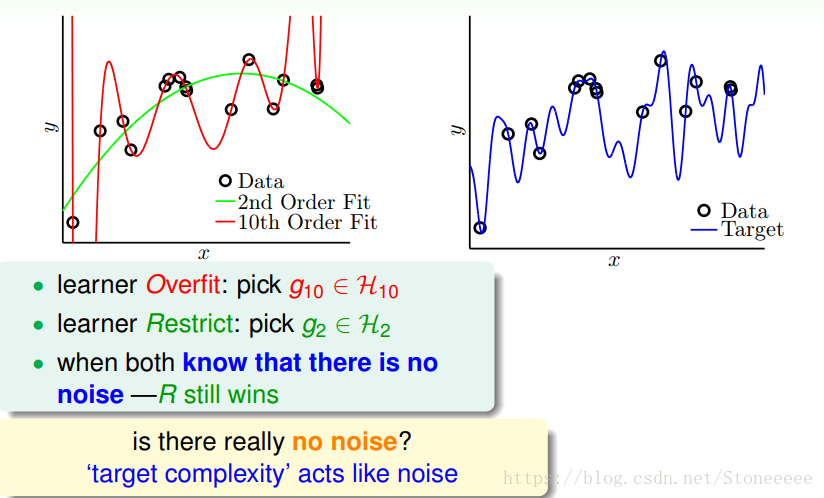
• 另一个例子中，目标函数是50阶多项式，且没有加入noise。这种情况下，我们发现仍然是2阶的模型拟合的效果更好一些，明明没有noise，为什么是这样的结果呢？
• 实际上，我们忽略了一个问题：这种情况真的没有noise吗？其实，当模型很复杂的时候，即50阶多项式的目标函数，无论是2阶模型还是10阶模型，都不能学习的很好，这种复杂度本身就会引入一种‘noise’；
• 所以，这种高阶无noise的问题，也可以类似于10阶多项式的目标函数加上noise的情况，只是二者的noise有些许不同，下面一部分将会详细解释。

三、Deterministic Noise

• 接下来用一个更详尽的例子来解释导致overfitting的原因，假设我们产生的数据分布由两部分组成：

• noise level 为${\sigma }^2$噪声ϵ，服从Gaussian分布

• $Q_f$阶的目标函数f(x)

• 同时，总的数据量是N
  

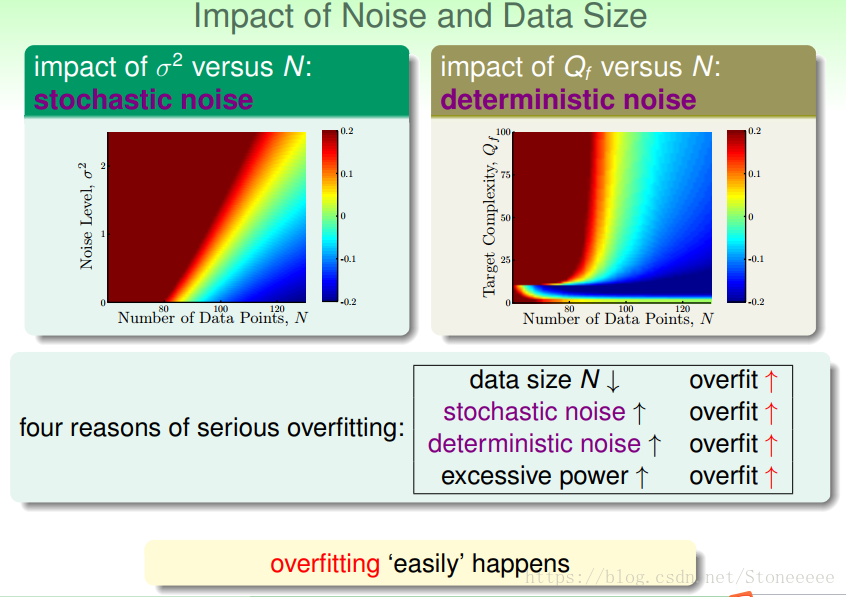
• 如果仍然使用2阶和10阶的模型进行fitting，那么衡量overfitting的办法为：$E_{out}(g_{10})-E_{out}(g_2)$
  

• 上图中蓝色代表overfitting程度很低，红色代表很严重的overfitting，同时横坐标都是数据量N，左图纵坐标是Noise level ${\sigma }^2$，右图纵坐标是targer function complexity $Q_f$；

• 从坐标中红色的区域能很清楚地看到导致overfitting的原因有如下：

• data size N ↓：learning curve告诉了我们同样的事情；

• stochastic noise↑：即随机noise的强度，这也容易理解；

• deterministic noise↑：Qf即模型复杂度也对overfit有很大影响，它和stochastic nose影响是相似的，所以我们把这种称之为deterministic noise；

• excessive power↑：其实就是我们常提到的$d_{vc}$
  

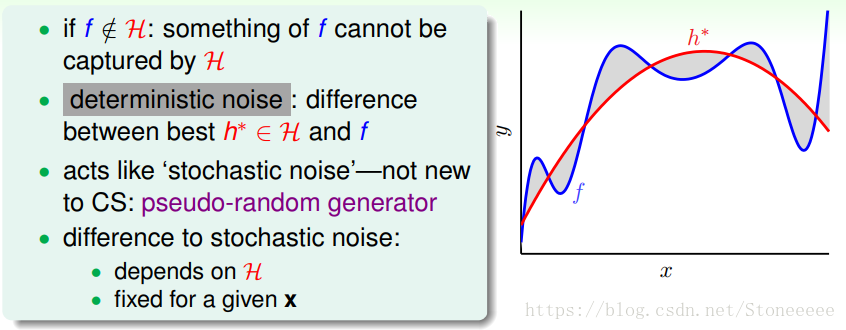
• 我们刚才解释了如果目标函数f(x)的复杂度很高的时候，那么跟有noise也没有什么两样;

• 因为目标函数很复杂，那么再好的hypothesis都会跟它有一些差距，我们把这种差距称之为deterministic noise。deterministic noise与stochastic noise不同，但是效果一样;

• 其实deterministic noise类似于一个伪随机数发生器，它不会产生真正的随机数，而只产生伪随机数。它的值与hypothesis有关，且固定点x的deterministic noise值是固定的。

四、Dealing with Overfitting
既然我们知道了overfitting的原因，那么我们应该如何来避免它呢？

• 同样以开车作为类比，避免overfitting的办法可能有如下：
• start from simple model
• data cleaning/pruning
• data hinting
• regularization
• validataion

regularization和validation我们之后的课程再介绍，本节课主要介绍简单的data cleaning/pruning和data hinting两种方法。

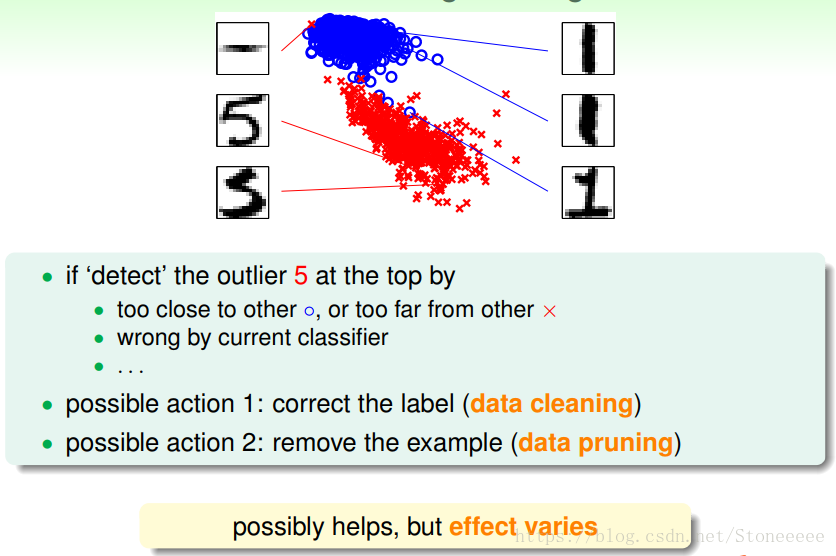
• 如果我们通过侦测知道data中某一个点是错误的，至于是通过什么办法侦测到有多种多样，那么可以做如下操作：
• 修改其label：我们称这种方法叫做data cleaning；
• 将其移除training data：我们称这种方法为data pruning；
• 这种方法通常只有在某一些情况下，才能发挥作用，特别是在这些点相比训练样本N很小的话，这种处理效果不太明显。
  
• data hinting是针对N不够大的情况，如果没有办法获得更多的训练集，那么data hinting就可以对已知的样本进行简单的处理、变换，从而获得更多的样本；
• 举个例子，数字分类问题，可以对已知的数字图片进行轻微的平移或者旋转，从而让N丰富起来，达到扩大训练集的目的。这种额外获得的例子称之为virtual examples；
• 但是要注意一点的就是，新获取的virtual examples可能不再是iid某个distribution。所以新构建的virtual examples要尽量合理，且是独立同分布的。

五、总结
本节课主要介绍了overfitting的概念，即当Ein很小，Eout很大的时候，会出现overfitting。详细介绍了overfitting发生的四个常见原因data size N、stochastic noise、deterministic noise和excessive power。解决overfitting的方法有很多，本节课主要介绍了data cleaning/pruning和data hinting两种简单的方法，之后的课程将会详细介绍regularization和validataion两种更重要的方法。