C++ 二分算法（2）

C++ 二分算法(1)和(2)的两个方法的区别无非就是一个是开区间 一个是闭区间

我们还是一样画图解决问题

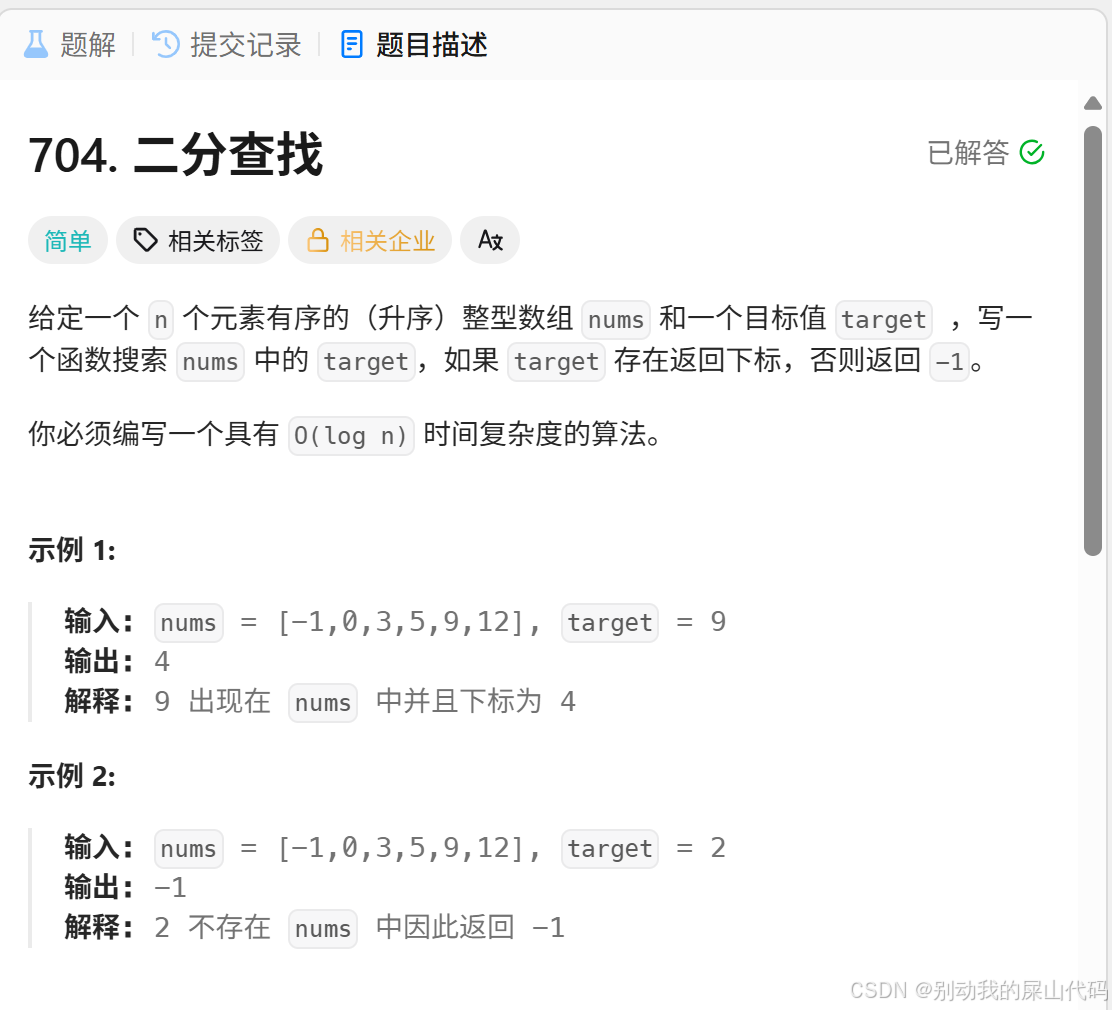
Example:nums={-1,0,1,3,5,9,12,17,23} target=5

相比第一种方法 第二种方法的

left的初始值是-1而不是0

right的初始值是nums.size()而不是nums.size()-1

也就是（-1，nums.size()）

转换成闭区间就是[0,nums.size()-1]和第一种方法表示的范围一模一样

第二种方法的本质是让left和right之间的区间是一个开区间

第一种方法的本质是让left和right之间的区间是一个闭区间

但是无论哪种方法表示出来的区间范围都是一样的 都是target可能取到值的区间

mid的取法和第一种方法是一致的

mid=   

最开始

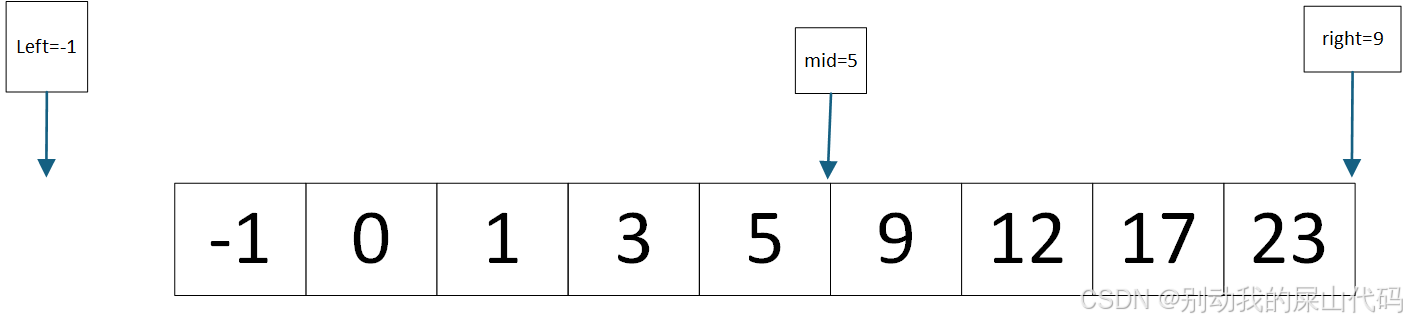
nums[mid]>target

所以这个时候

说明   target不可能存在于mid和right之间即[5,9)  

转换成闭区间就是[5,8]

这里的5和8表示的数组的相对位置

可以近似理解成数组的下标

也就是target只可能存在于left和mid之间（-1,5）

由于在第二种方法中left和right本身就指向的是开区间

且left和right的范围始终是target可能的取值范围

所以这个地方要对right进行调整

直接 right=mid就行了

mid再重新计算即可

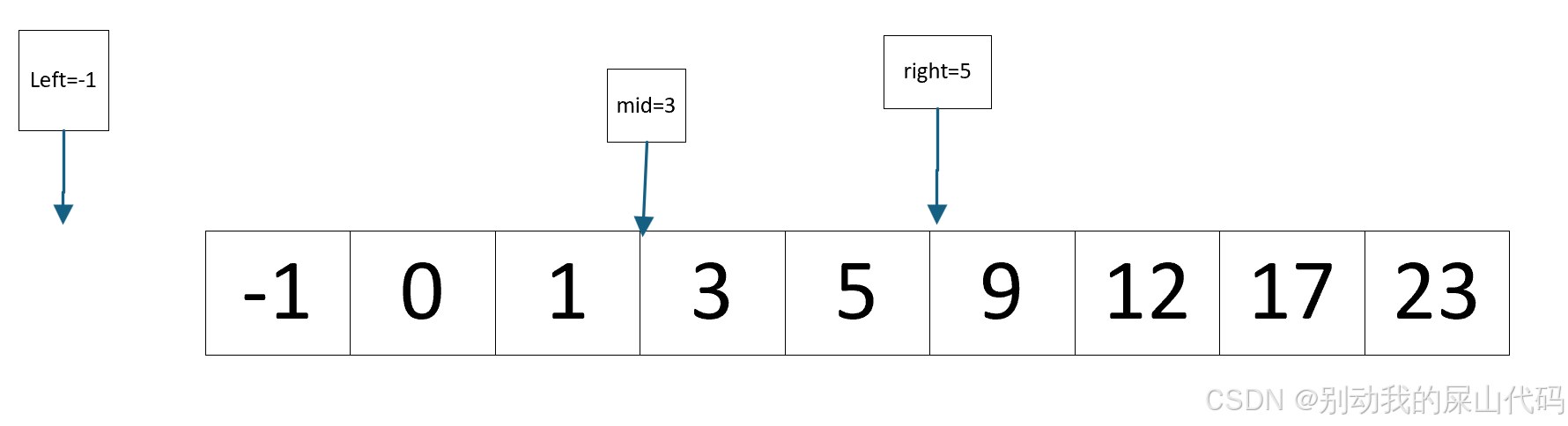
此时 nums[mid]<target

说明   target不可能存在于下图left和mid之间即(-1,3]

也就是说target只可能存在于mid到right 之间 即(3,5)

由于在第二种方法中left和right本身就指向的是开区间

且left和right的范围始终是target可能的取值范围

所以这个地方要对left进行调整
直接 left=mid就行了

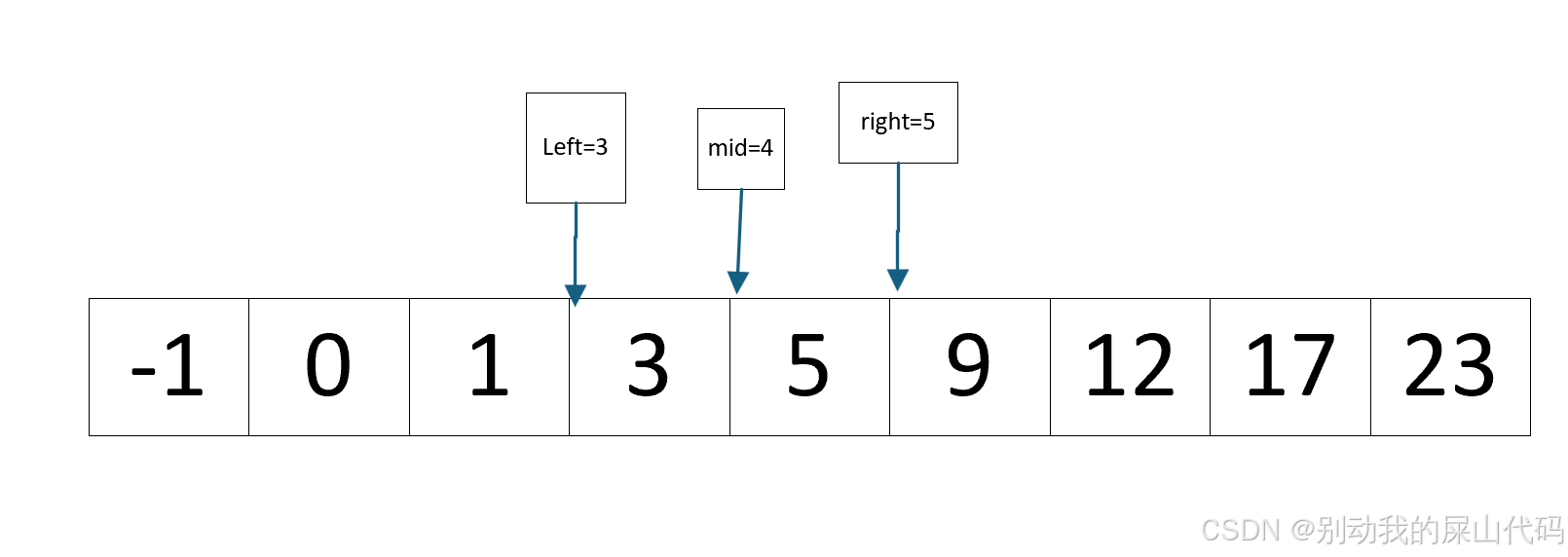
这个时候nums[mid]=target 所以就找到了

因此我么就可以把二分算法的核心思路写下来

while (停止条件) {
	mid = left + (right - left) / 2;
	if (nums[mid] > target) {
		right = mid;
	}
	else if (nums[mid] < target) {
		left = mid;
	}
	else {
		return mid;
	}
}

但是思考一下 什么时候停停下来最好？？？

方法一中

停止条件 :left>right    区间:[left,right]

但是方法二中和方法一不一样的是

方法1中while循环每执行一次

下面其中一种情况必然会发生

left向左至少加一 或者 right至少减一

所以left和right一定会相遇 

但是方法二不一定

有可能执行一次while的时候left或者right原地踏步

这样就可能陷入死循环

当left 和 right 有一端是mid的情况就可能发生

比如

left=1 mid=1 right=2  nums[mid]  target

left=mid=1;  mid=left+(right-mid)/2=1+0=1 right=2;

陷入死循环了 

有兴趣可以自己取调试查看

nums={-1,0,3,5,9,12}  target=2

那么这个如果target不存在与nums中

我们该如何设置while循环的停止条件呢？？？

方法一我们停止条件本质上是什么？？？

本质上是我把数组所有区间都遍历了

当方法1while循环停止的时候

left>right此时 [left,right]这个区间就不存在 所有所有的区间都被遍历了

但是如果是闭区间（left,right） 当left和right什么关系的时候

这个区间不存在？？？

我们可以先把这个闭区间转换成开区间

[left+1,right-1]

也就是停止条件是left+1>right-1

所以停止条件就是left+2>right

所以进入while条件就是left+2<=right

当然写成left+1<right同理

其实这不就是开区间的两端不能相邻嘛

相邻了 那么这个区间就没有值了 

所有区间就都被遍历过了 所以这个时候while循环就结束了呀

class Solution {
public:
	int search(vector<int>nums, int target) {
		int left = -1;          // 初始左边界（开区间左侧，不包含）
		int right = nums.size(); // 初始右边界（开区间右侧，不包含）
		int mid;
		// 循环条件：开区间内还有元素（left和right不相邻）
		while (left+1  < right) {
			 mid = left + (right - left) / 2; // 计算中间位置
			int num = nums[mid];

			if (num == target) {
				return mid; // 找到目标，返回索引
			}
			else if (num < target) {
				// 目标在mid右侧，更新左边界为mid（开区间左侧右移）
				left = mid;
			}
			else {
				// 目标在mid左侧，更新右边界为mid（开区间右侧左移）
				right = mid;
			}
		}
		// 循环结束后，开区间内无元素，目标不存在
		return -1;
	}
};

当然你如果说像第一种方法一样 如果我要写其他条件作为while循环的结束条件

也许可以 但是没必要 那样只会将一个简单的问题复杂化