经典集合
定义
当前有n个元素,元素可以属于某个集合,也可以不属于某个集合,这样的属于关系为布尔型,要么完全属于,要么完全不属于。
比如当前有四个人:小明,李丽,大红,李雷
同时存在老年人集合:{李丽,大红,李雷},则由该老年人集合的信息可知,小明完全不属于老年人,而李丽等人完全属于老年人。
我们接下来将设 U \mathbb{U} U为论域,而 x x x为 U \mathbb{U} U中的元素。而 A A A为经典集合,且 A ⊆ U A\subseteq\mathbb{U} A⊆U。每个元素 x ∈ A x\in{A} x∈A或 x ∉ A x\notin{A} x∈/A。若用有序对来表示元素与集合的从属关系,则 ( x , 0 ) , ( x , 1 ) (x,0), (x,1) (x,0),(x,1)分别表示 x x x不属于和属于 A A A。
若两个集合包含完全相同的元素,则称它们相等。集合A的基数代表集合元素的数量,通常表示为 ∣ A ∣ |A| ∣A∣,例如之前的老年人集合, ∣ A ∣ = 3 |A|=3 ∣A∣=3,同时,空集的基数为0,表示为 ∅ \emptyset ∅.
子集
若集合 A A A中所有元素均属于集合 B B B,则称 A A A为 B B B的子集, A ⊆ B A\subseteq{B} A⊆B。若满足上述条件的同时,A不等于B,则称 A A A为 B B B的真子集, A ⊂ B A\sub{B} A⊂B。
运算
有几种运算可以运算于集合,这里仅考虑基本运算。
并集
两个集合 A A A和 B B B的并集 A ∪ B A\cup{B} A∪B,包含A和B的所有元素。我们可以定义为 A ∪ B = { x ∣ ( x ∈ A ) o r ( x ∈ B ) } A\cup{B}=\{x|(x\in{A})or(x\in{B})\} A∪B={x∣(x∈A)or(x∈B)},且有以下性质:
A
∪
B
=
B
∪
A
A\cup{B}={B}\cup{A}
A∪B=B∪A
A
⊆
A
∪
B
A\subseteq{A}\cup{B}
A⊆A∪B
A
∪
A
=
A
{A}\cup{A}=A
A∪A=A
A
∪
∅
=
A
{A}\cup\emptyset=A
A∪∅=A
交集
两个集合 A A A和 B B B的并集 A ∩ B A\cap{B} A∩B,包含 A A A和 B B B的共同元素。我们可以定义为 A ∩ B = { x ∣ ( x ∈ A ) a n d ( x ∈ B ) } A\cap{B}=\{x|(x\in{A})and(x\in{B})\} A∩B={x∣(x∈A)and(x∈B)}。 A A A和 B B B没有共同元素的情况下,它们的并集为空集。交集有以下性质:
A
∩
B
=
B
∩
A
A\cap{B}={B}\cap{A}
A∩B=B∩A
A
∪
B
⊆
A
{A}\cup{B}\subseteq{A}
A∪B⊆A
A
∩
A
=
A
{A}\cap{A}={A}
A∩A=A
A
∩
∅
=
∅
{A}\cap{\empty}={\empty}
A∩∅=∅
补集
A
A
A在
B
B
B中的相对补集(或称为集合论差分)为
B
B
B集合中有的元素,同时
A
A
A集合中没有的元素。我们将其表述为
B
−
A
B-A
B−A或
B
\
A
B\backslash{A}
B\A,我们定义为
B
−
A
=
{
x
∣
(
x
∈
B
)
a
n
d
n
o
t
(
x
∈
A
)
}
B-A=\{x|(x\in{B})\space and \space not \space(x\in{A})\}
B−A={x∣(x∈B) and not (x∈A)}.
我们将
U
−
A
\mathbb{U}-A
U−A称为
A
A
A的绝对补集或简单补集,表示为
A
′
A^{'}
A′或
A
c
A^{c}
Ac。
我们有以下性质:
A
∪
A
c
=
U
A\cup A^c=\mathbb{U}
A∪Ac=U
A
∩
A
c
=
∅
A\cap A^c=\empty
A∩Ac=∅
(
A
c
)
c
=
A
(A^c)^c=A
(Ac)c=A
A
−
A
=
∅
A-A=\empty
A−A=∅
A
−
B
=
A
∩
B
c
A-B=A\cap B^c
A−B=A∩Bc
模糊集理论
在不确定情况下处理集合的一种独特方法是使用模糊集理论。该理论的主要目标是用一种方法来表达和解决那些过于复杂或定义不清而不适用于传统布尔型集合理论分析的问题。在该理论下,论域中的元素对于一个集合的隶属关系是处于是和非之间的,即渐进的。而经典集合论中,元素对于一个集合的隶属关系是明确的,要么属于,要么不属于。
在现实中的模糊性需要用数学语言进行描述的时候,就可以使用模糊集,并用主观知识来定义元素对于集合的隶属度。有助于减轻对不确定领域知识的编码要求。
定义
模糊集可以定义为一组有序对
A
=
{
x
,
μ
A
(
x
)
∣
x
∈
U
}
A=\{ x,μ_A(x)|x\in\mathbb{U}\}
A={x,μA(x)∣x∈U}。函数
μ
A
(
x
)
μ_A(x)
μA(x)被称为
x
x
x对于
A
A
A的隶属度,论域可以是离散的,也可以是连续的。任何包含至少一个隶属度为1的元素的模糊集称为正规(normal)模糊集。
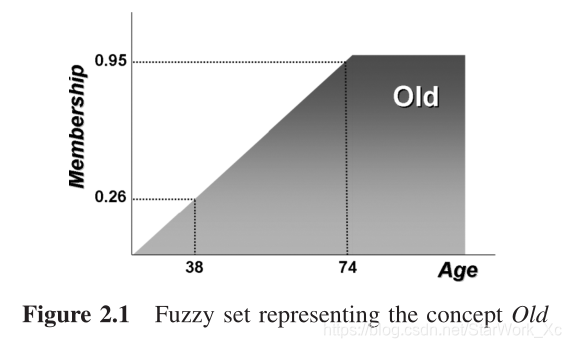
这里我们定义了一个属于Old集合的隶属函数。可知38岁的人与该集合的隶属度约为0.26,74岁的人与该集合的隶属度约为0.95,他们都属于Old这个模糊集合。
由于隶属函数的分布通常是主观的。一种构造隶属度函数的方法是使用投票模式,这种方法生成的模糊集基于现实。另一种方法是变量概率分布的积分。
运算
模糊集上最基本的运算是并集,交集和补集。这些是经典集合论中对应运算的模糊拓展。
模糊交集
两个模糊集 A A A和 B B B的并集(t-norm),一般是由零到一的范围的二元运算。就如以下形式:
t : [ 0 , 1 ] × [ 0 , 1 ] → [ 0 , 1 ] t:[0,1]\times[0,1]→[0,1] t:[0,1]×[0,1]→[0,1]
并集运算对于论域中的所有元素 x x x,以 x x x在模糊集 A A A和 B B B中的隶属度作为参数,得出构成 A A A和 B B B交集的集合中元素的隶属度等级。
μ A ∩ B ( x ) = t [ μ A ( x ) , μ B ( x ) ] μ_{A\cap B}(x)=t[μ_A(x),μ_B(x)] μA∩B(x)=t[μA(x),μB(x)]
不同的算子 t t t会使运算方法不同,但所有算子的运算都必须遵从以下公理:
∙ t ( x , 1 ) = x \bullet \space t(x,1)=x ∙ t(x,1)=x (边界条件)
∙ y ≤ z → t ( x , y ) ≤ t ( x , z ) \bullet \space y\leq z \to t(x,y) \leq t(x,z) ∙ y≤z→t(x,y)≤t(x,z) (单调性)
∙ t ( x , y ) = t ( y , x ) \bullet \space t(x,y)=t(y,x) ∙ t(x,y)=t(y,x) (交换性)
∙ t ( x , t ( y , z ) ) = t ( t ( x , y ) , z ) \bullet \space t(x,t(y,z))=t(t(x,y),z) ∙ t(x,t(y,z))=t(t(x,y),z) (结合性)
以下是模糊交集常用的t-norm:
t ( x , y ) = m i n ( x , y ) t(x,y)=min(x,y) t(x,y)=min(x,y) (标准交集)
t ( x , y ) = x ∗ y t(x,y)=x*y t(x,y)=x∗y (代数乘积)
t ( x , y ) = m a x ( 0 , x + y − 1 ) t(x,y)=max(0,x+y-1) t(x,y)=max(0,x+y−1) (界限差)
模糊并集
与模糊交集大致相同,两个模糊集A和B的模糊并集 ( t − c o n o r m o r s − n o r m ) (t-conorm or s-norm) (t−conormors−norm)由一个函数来指定:
s : [ 0 , 1 ] × [ 0 , 1 ] → [ 0 , 1 ] s:[0,1]\times[0,1]\to[0,1] s:[0,1]×[0,1]→[0,1]
μ A ∪ B ( x ) = s [ μ A ( x ) , μ B ( x ) ] μ_{A\cup{B}}(x)=s[μ_A(x),μ_B(x)] μA∪B(x)=s[μA(x),μB(x)]
模糊并集运算需满足以下公理:
∙ s ( x , 0 ) = x \bullet \space s(x,0)=x ∙ s(x,0)=x (边界条件)
∙ y ≤ z → s ( x , y ) ≤ s ( x , z ) \bullet \space y\leq z \to s(x,y) \leq s(x,z) ∙ y≤z→s(x,y)≤s(x,z) (单调性)
∙ s ( x , y ) = s ( y , x ) \bullet \space s(x,y)=s(y,x) ∙ s(x,y)=s(y,x) (交换性)
∙ s ( x , s ( y , z ) ) = s ( s ( x , y ) , z ) \bullet \space s(x,s(y,z))=s(s(x,y),z) ∙ s(x,s(y,z))=s(s(x,y),z) (结合性)
下面常被用作模糊并集运算的t-conorm:
s ( x , y ) = m a x ( x , y ) s(x,y)=max(x,y) s(x,y)=max(x,y) (标准并集)
s ( x , y ) = x + y − x ∗ y s(x,y)=x+y-x*y s(x,y)=x+y−x∗y (代数和)
s ( x , y ) = m i n ( 1 , x + y ) s(x,y)=min(1,x+y) s(x,y)=min(1,x+y) (界限和)
考虑到其易于计算,最常用的并集和交集运算是标准并集和标准交集。此后若没有特别提到,均使用这样的计算方法。
模糊补集
模糊集 A A A的补集由一个函数指定:
c : [ 0 , 1 ] → [ 0 , 1 ] c:[0,1]\to[0,1] c:[0,1]→[0,1]
μ c A ( x ) = μ ¬ A ( x ) = c [ μ A ( x ) ] μ_{cA}(x)=μ_{\neg A}(x)=c[μ_A(x)] μcA(x)=μ¬A(x)=c[μA(x)]
符合下述公理:
∙
c
(
0
)
=
1
,
c
(
1
)
=
0
\bullet c(0)=1 ,c(1)=0
∙c(0)=1,c(1)=0 (边界情况)
∙
∀
a
,
b
∈
[
0
,
1
]
\bullet \forall a,b\in [0,1]
∙∀a,b∈[0,1] 若
a
≤
b
a\leq b
a≤b 且
c
(
a
)
≥
c
(
b
)
c(a)\geq c(b)
c(a)≥c(b) (单调性)
∙
c
\bullet c
∙c是一个连续函数 (连续性)
∙
c
\bullet c
∙c是 对合的
(
c
(
c
(
a
)
=
a
)
)
(c(c(a)=a))
(c(c(a)=a))(对合性)
模糊集的补可以用多种方法来表示:通常会用 ¬ A \neg A ¬A和 A ‾ \overline A A来表述。也可以用 A c A^c Ac来表述,如同经典集合论那样。模糊补集的一个标准定义为:
μ c A ( x ) = 1 − μ A ( x ) μ_{cA}(x)=1-μ_A(x) μcA(x)=1−μA(x)
模糊关系及合成
除了上述定义的三个算子外,许多传统的数学函数都可以推广至模糊值,使用可拓原理(extension principle)它提供了经典数学概念到模糊环境的一般拓展。这一原则如下所述:
若一个n元函数
f
f
f映射了笛卡尔积
X
1
×
X
2
×
.
.
.
×
X
n
X_1\times X_2\times ...\times X_n
X1×X2×...×Xn至论域
Y
Y
Y上,使
y
=
f
(
x
1
,
x
2
,
.
.
.
,
x
n
)
y=f(x_1,x_2,...,x_n)
y=f(x1,x2,...,xn)且
A
1
,
A
2
,
.
.
.
,
A
n
A_1,A_2,...,A_n
A1,A2,...,An分别为
n
n
n个在子空间
X
1
,
X
2
,
.
.
.
,
X
n
X_1,X_2,...,X_n
X1,X2,...,Xn上的模糊集,由隶属度分布
μ
A
i
(
X
i
)
,
i
=
1
,
2
,
.
.
.
,
n
μ_{A_i}(X_i),i=1,2,...,n
μAi(Xi),i=1,2,...,n来表征。可归纳出论域
Y
Y
Y上的模糊集,求笛卡尔积空间中最高的隶属度,
y
y
y为该隶属度下各个空间中,如下所述:
μ B ( y ) = { m a x { x 1 , . . . , x n , y = f ( x 1 , . . . , x n ) } m i n ( μ A 1 ( x 1 ) , . . . , μ A n ( x n ) ) i f f − 1 ( Y ) ≠ ∅ 0 i f f − 1 ( Y ) = ∅ μ_{B}(y)=\begin{cases} max_{ \{ x_1,...,x_n,y=f(x_1,...,x_n)\}}min(μ_{A_1}(x_1),...,μ_{A_n}(x_n)) & if\space f^{-1}(Y)\neq\empty \\ 0 & if\space f^{-1}(Y)=\empty\end{cases} μB(y)={max{x1,...,xn,y=f(x1,...,xn)}min(μA1(x1),...,μAn(xn))0if f−1(Y)=∅if f−1(Y)=∅
举例:现有三个子空间,擅长的计算机语言 X 1 X_1 X1{C++,Python,Java},精通方向 X 2 X_2 X2{图论,数论,动态规划},学习能力 X 3 X_3 X3{强,中,弱},当前有三个样例{小明,小强,小红}。
| C++ | Python | Java | |
|---|---|---|---|
| 小明 | 0.9 | 0.7 | 0.8 |
| 小强 | 0.4 | 0.7 | 0.9 |
| 小红 | 0.9 | 0.7 | 0.1 |
| 图论 | 数论 | 动规 | |
|---|---|---|---|
| 小明 | 0.2 | 0.5 | 0.3 |
| 小强 | 0.6 | 0.2 | 0.4 |
| 小红 | 0.3 | 0.5 | 0.3 |
| 学强 | 学中 | 学弱 | |
|---|---|---|---|
| 小明 | 0.5 | 0.5 | 0.0 |
| 小强 | 0.1 | 0.8 | 0.1 |
| 小红 | 0.8 | 0.4 | 0.0 |
在论域Y中,有
3
∗
3
∗
3
3*3*3
3∗3∗3种粗糙集,倘若要求小明对【擅长C++,精通图论,学习能力强】粗糙集的隶属度,根据当前标准算子的运算法则,可知小明对于该粗糙集的隶属度为
m
i
n
(
0
,
9
,
0.2
,
0.5
)
=
0.2
min(0,9,0.2,0.5)=0.2
min(0,9,0.2,0.5)=0.2
而求最大隶属度中,小明【擅长C++,精通数论,学习能力强】粗糙集的隶属度最高,因而以上
μ
B
(
y
)
=
0.5
μ_{B}(y)=0.5
μB(y)=0.5。
如果 U U U是 X 1 X_1 X1到 X 2 X_2 X2的关系,并且 V V V为 X 2 X_2 X2到 X 3 X_3 X3的关系,那么 U U U和 V V V的组合就是 x 1 x1 x1到 x 3 x3 x3的模糊关系,其由 U ∘ V U\circ V U∘V来表示,并由下式定义:
μ U ∘ V ( x 1 , x 3 ) = max x 2 ∈ X 2 m i n ( μ U ( x 1 , x 2 ) , μ v ( x 2 , x 3 ) ) , x 1 ∈ X 1 , x 3 ∈ X 3 μ_{U\circ V}(x_1,x_3)={\max\limits_{x_2\in X_2}min(μ_U (x_1,x_2),μ_v(x_2,x_3))},x_1\in X_1,x_3\in X_3 μU∘V(x1,x3)=x2∈X2maxmin(μU(x1,x2),μv(x2,x3)),x1∈X1,x3∈X3
我们将用矩阵的方法来表示二元模糊关系,例如,下面的矩阵
P
P
P可以用来表示一个电脑游戏爱好者,比起传统游戏更喜欢多媒体游戏,无论是工作站还是个人电脑。

假设该爱好者更喜欢基于键盘的游戏,而不是基于鼠标的,那么另一个关系Q,可以用来描述这种偏好。
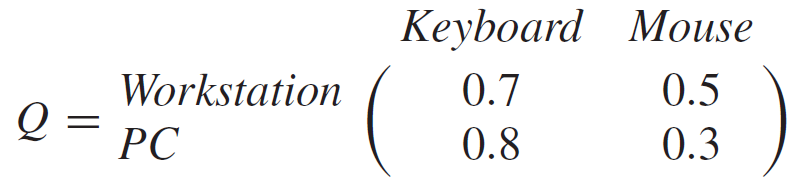
给定这两个关系,可以得到一个组合关系,如下所示:

这一关系表明,该爱好者尤其喜好基于键盘的多媒体游戏。
近似推理.
模糊关系和模糊关系组合构成了近似推理的基础,有时我们也称其为模糊推理。非正式地说,近似推理指从一系列不精准的前提中推断出可能不精准的结论的过程。执行这种推理的系统建立在一组模糊产生(如果-那么)规则的基础上,这些规则提供了一种从经验关联或者经验中获得知识的正规方式。这样的系统运行在一组给定的集合上,并允许某些规则的前提属性(通常是部分)实例化。
例如,一个规则为:
如果 x x x 属于 A i A_i Ai,并且 y y y 属于 B i B_i Bi,则 z z z 属于 C i C_i Ci
这一规则支配了前提属性 x x x和 y y y与结论属性 z z z之间的特定关系,可以被翻译为模糊关系 R i R_i Ri
μ R i ( x , y , z ) = m i n ( μ A i ( x ) , μ B i ( y ) , μ C i ( z ) ) μ_{R_i}(x,y,z)=min(μ_{A_i}(x),μ_{B_i}(y),μ_{C_i}(z)) μRi(x,y,z)=min(μAi(x),μBi(y),μCi(z))
在这里, A i , B i , C i A_i,B_i,C_i Ai,Bi,Ci分别是定义属性为 x , y , z x,y,z x,y,z的论域 X , Y , Z X,Y,Z X,Y,Z的模糊集。有了这个关系,如果前提属性 x x x和 y y y实际取对模糊集 A ′ A^{'} A′和 B ′ B^{'} B′的关系,则结论属性的新模糊值可以通过应用推理的合成规则来获得:
C ′ = ( A ′ × B ′ ) ∘ R i C^{'}=(A^{'}\times B^{'})\circ R_i C′=(A′×B′)∘Ri
或表述为,
μ c ′ ( z ) = max x ∈ X , y ∈ Y min ( μ A ′ ( x ) , μ B ′ ( y ) , μ R i ( x , y , z ) ) μ_{c^{'}}(z)=\max\limits_{x\in X,y\in Y}\min(μ_{A^{'}}(x),μ_{B^{'}}(y),μ_{R_i}(x,y,z)) μc′(z)=x∈X,y∈Ymaxmin(μA′(x),μB′(y),μRi(x,y,z))
我们用简单的例子来解释。
设存在论域T(温度)={0,20,40,60,80,100}和P(压力)={1,2,3,4,5,6,7}上定义模糊子集的(枚举型描述)隶属函数:
μ A ( 温 度 高 ) = 0 0 + 0.1 20 + 0.3 40 + 0.6 60 + 0.85 80 + 1 100 μ_A(温度高)=\frac{0}{0}+\frac{0.1}{20}+\frac{0.3}{40}+\frac{0.6}{60}+\frac{0.85}{80}+\frac{1}{100} μA(温度高)=00+200.1+400.3+600.6+800.85+1001
μ B ( 压 力 大 ) = 0 1 + 0.1 2 + 0.3 3 + 0.5 4 + 0.7 5 + 0.85 6 + 1 7 μ_B(压力大)=\frac{0}{1}+\frac{0.1}{2}+\frac{0.3}{3}+\frac{0.5}{4}+\frac{0.7}{5}+\frac{0.85}{6}+\frac{1}{7} μB(压力大)=10+20.1+30.3+40.5+50.7+60.85+71
(即温度为0度时,隶属度为0,温度为20度时,隶属度为0.1,以此类推)
现在的条件是温度高,则压力大,带入之前的关系式:
μ R i ( x , y ) = m i n ( μ T i ( x ) , μ P i ( y ) ) μ_{R_i}(x,y)=min(μ_{T_i}(x),μ_{P_i}(y)) μRi(x,y)=min(μTi(x),μPi(y))
则可知论域内任意一点的关系隶属度。
若我们根据经验得知而温度较高的情况,且有温度较高,压力也较高的推论,我们希望根据先前的已知关系推理出压力较高时的隶属情况。则先定义温度较高的隶属函数:
μ A ( 温 度 高 ) = 0.1 0 + 0.15 20 + 0.4 40 + 0.75 60 + 1 80 + 0.8 100 μ_A(温度高)=\frac{0.1}{0}+\frac{0.15}{20}+\frac{0.4}{40}+\frac{0.75}{60}+\frac{1}{80}+\frac{0.8}{100} μA(温度高)=00.1+200.15+400.4+600.75+801+1000.8
代入推理式则有:
μ P ′ ( y ) = max x ∈ X , y ∈ Y min ( μ T ′ ( x ) , μ R i ( x , y ) ) μ_{P^{'}}(y)=\max\limits_{x\in X,y\in Y}\min(μ_{T^{'}}(x),μ_{R_i}(x,y)) μP′(y)=x∈X,y∈Ymaxmin(μT′(x),μRi(x,y))
根据该推理式即可构建出压力较高的隶属函数。
上述定义的关系隶属度的意义是当前样本状态(x,y)对当前关系条件的相近度,与原状态越相近就说明当前状态下关系的可信度越大,关系隶属度也越高。
一个近似推理系统通常不会只使用一个特定的规则,而是使用一个集合。给定一组规则,在该系统中,可以采用两种不同的方法来实现推理·,两者都依赖于上面给出推理组合规则的使用。第一种方法是再找到与整个规则集相关联的整体关系之后应用组合规则。第二种规则是先将组合规则局部应用,最后再将应用的结果聚合起来,形成整体结果。
给定K个(if-then)规则,给定N个前提属性 x 1 , x 2 , . . . , x n x_1,x_2,...,x_n x1,x2,...,xn,和一个推理属性 y y y。同时逻辑连接词严格从左至右。下面将给出两种组合推理的方法。
方法一:整体解释关系的推理
步骤①: 对于每一个规则,计算它的模糊关系隶属度。例如当前我们给定两条规则 ( K = 2 , N = 3 ) (K=2,N=3) (K=2,N=3):
[1] 若
x
1
x_1
x1属于
A
1
A_1
A1,
x
2
x_2
x2不属于
B
1
B_1
B1或者
x
3
x_3
x3属于
C
1
C_1
C1,则
y
y
y属于
D
1
D_1
D1
[2] 若
x
1
x_1
x1不属于
A
2
A_2
A2或
x
2
x_2
x2属于
B
2
B_2
B2,且
x
3
x_3
x3不属于
C
2
C_2
C2,则
y
y
y属于
D
2
D_2
D2
分别计算它们的模糊关系隶属度,可以由下面表述:
R
1
(
x
1
,
x
2
,
x
3
,
y
)
=
min
{
max
{
min
{
μ
A
1
(
x
1
)
,
1
−
μ
B
1
(
x
2
)
}
,
μ
C
1
(
x
3
)
}
,
μ
D
1
(
y
)
}
R_1(x_1,x_2,x_3,y)=\min\{\max\{\min\{μ_{A_1}(x_1),1-μ_{B_1}(x_2)\},μ_{C_1}(x_3)\},μ_{D_1}(y)\}
R1(x1,x2,x3,y)=min{max{min{μA1(x1),1−μB1(x2)},μC1(x3)},μD1(y)}
R
2
(
x
1
,
x
2
,
x
3
,
y
)
=
min
{
min
{
m
a
x
{
1
−
μ
A
2
(
x
1
)
,
μ
B
2
(
x
2
)
}
,
1
−
μ
C
2
(
x
3
)
}
,
1
−
μ
D
2
(
y
)
}
R_2(x_1,x_2,x_3,y)=\min\{\min\{max\{1-μ_{A_2}(x_1),μ_{B_2}(x_2)\},1-μ_{C_2}(x_3)\},1-μ_{D_2}(y)\}
R2(x1,x2,x3,y)=min{min{max{1−μA2(x1),μB2(x2)},1−μC2(x3)},1−μD2(y)}
步骤②: 结合个体模糊关系,形成整体的综合关系,表述如下:
R ( x 1 , x 2 , . . . , x N , y ) = max k ∈ { 1 , 2 , . . . , K } R k ( x 1 , x 2 , . . . , x N , y ) R_(x_1,x_2,...,x_N,y)=\max\limits_{k\in \{1,2,...,K\}}R_k(x_1,x_2,...,x_N,y) R(x1,x2,...,xN,y)=k∈{1,2,...,K}maxRk(x1,x2,...,xN,y)
步骤③: 应用整体规则,定义每个前提属性的隶属度值\函数后,即可得到结论属性的推理模糊隶属度值\函数 D D D。表述如下:
μ D ( y ) = max x 1 , x 2 , . . . , x n min { μ A ( x 1 ) , μ B ( x 2 ) , . . . , μ C ( x N ) , μ R { x 1 , x 2 , . . . , x N , y } } μ_D(y)=\max\limits_{x_1,x_2,...,x_n}\min \{μ_A(x_1),μ_B(x_2),...,μ_C(x_N),μ_R\{x_1,x_2,...,x_N,y\}\} μD(y)=x1,x2,...,xnmaxmin{μA(x1),μB(x2),...,μC(xN),μR{x1,x2,...,xN,y}}
方法二:通过局部关系进行推理
步骤①: 与方法一中的相同。
步骤②: 给定每个前提属性的隶属度值\函数,对于每一个子规则 R k R_k Rk,计算它们之下的目标模糊隶属度\函数 μ D k ( y ) μ_{D_k}(y) μDk(y)。表述如下:
μ D k ( y ) = max x 1 , x 2 , . . . , x N min { μ A ( x 1 ) , μ B ( x 2 ) , . . . , μ C ( x N ) , μ R k ( x 1 , x 2 , . . . , x N , y ) } μ_{D_k}(y)=\max\limits_{x_1,x_2,...,x_N}\min\{μ_A(x_1),μ_B(x_2),...,μ_C(x_N),μ_{R_k}(x_1,x_2,...,x_N,y)\} μDk(y)=x1,x2,...,xNmaxmin{μA(x1),μB(x2),...,μC(xN),μRk(x1,x2,...,xN,y)}
步骤③: 通过汇聚每个规则推导出的模糊隶属度\函数,计算结论属性的总体模糊隶属度\函数。表述为:
μ D ( y ) = max k , k ∈ { 1 , 2 , . . . , K } μ D k ( y ) μ_D(y)=\max\limits_{k,k\in \{1,2,...,K\}}μ_{D_k}(y) μD(y)=k,k∈{1,2,...,K}maxμDk(y)
去模糊化
有很多去模糊化的方法,它们各有优缺。下面简要总结两种广泛使用的方法:
重心法:从推断出的结论属性 y y y的模糊值 D D D中找到几何中心 y ^ \hat y y^作为去模糊化值,即:
y ^ = ∑ y μ D ( y ) ∑ μ D ( y ) \hat y =\frac{\sum yμ_D(y)}{\sum μ_D(y)} y^=∑μD(y)∑yμD(y)
极大值均值法: 取D中隶属度最大的值作为去模糊化的解,若有多个最大隶属度,则取它们的平均值作为去模糊化值。
模糊-粗糙集理论
本节涵盖了粗糙集理论的模糊拓展背后的基本概念。
粗糙集理论的成功运行依赖于离散数据,是该方法的一个显著缺陷。处理这一问题的较好方法是使用模糊粗糙集。由于还需要定义模糊集隶属度函数,主观判断并不能完全消除。不过,该方法在处理实值数据时具有高度的灵活性,能基于当前存在的模糊性和不精确性有效建模。
模糊等价类
如同粗糙集中的明确等价类,模糊等价类是模糊粗糙集的中心。明确等价类的概念可以拓展为论域中的模糊相似关系 S S S,它决定了两个元素的相似程度。比如,如果 μ S ( x , y ) = 0.9 μ_S(x,y)=0.9 μS(x,y)=0.9,那么对象 x x x和 y y y可以说是非常相似的。
利用模糊相似关系,可以为与 x x x相似的对象定义模糊等价类 [ x ] s [x]_s [x]s:
μ [ x ] s ( y ) = μ s ( x , y ) μ_{[x]_s}(y)=μ_s(x,y) μ[x]s(y)=μs(x,y)
以下公理在任意一个模糊等价类
F
F
F中应当成立:
∙
∃
x
,
μ
F
(
x
)
=
1
\bullet \exist x,μ_F(x)=1
∙∃x,μF(x)=1 (
μ
F
μ_F
μF经过归一化)
∙
μ
F
(
x
)
∧
μ
S
(
x
,
y
)
≤
μ
F
(
y
)
\bullet μ_F(x)\wedgeμ_S(x,y)\leq μ_F(y)
∙μF(x)∧μS(x,y)≤μF(y)
∙
μ
F
(
x
)
∧
μ
F
(
y
)
≤
μ
S
(
x
,
y
)
\bullet μ_F(x)\wedgeμ_F(y)\leq μ_S(x,y)
∙μF(x)∧μF(y)≤μS(x,y)
第一个公理对应的是等价类非空。
第二个公理说明:
y
y
y的邻域中的元素在
y
y
y的等价类中。
第三个公理说明
F
F
F中的任意两个元素通过
S
S
S是相关的,当关系不模糊时,这个定义退化为等价类的原定义。
由论域的模糊划分,产生的规范模糊集的集合可以起到模糊等价类的作用。对于一个论域 U \mathbb{U} U,我们可以通过 Q Q Q中的属性进行划分: U / Q = { { 1 , 3 , 6 } , { 2 , 4 , 5 } } \mathbb{U}/Q=\{\{1,3,6\},\{2,4,5\}\} U/Q={{1,3,6},{2,4,5}}。在粗糙集合论中,每个元素各自属于一个等价类。但是在模糊-粗糙集理论中,一个元素对于一个等价类存在隶属度。
模糊粗糙集
在文献中,每个模糊等价类对目标集合的模糊下近似隶属度和模糊上近似隶属度被定义为:
μ
P
‾
X
(
F
i
)
=
i
n
f
x
max
{
1
−
μ
F
i
(
x
)
,
μ
X
(
x
)
}
,
∀
i
μ_{\underline{P}X}(F_i)=inf_x\max\{1-μ_{F_i}(x),μ_X(x)\},\space \forall{i}
μPX(Fi)=infxmax{1−μFi(x),μX(x)}, ∀i
μ
P
‾
X
(
F
i
)
=
s
u
p
x
min
{
μ
F
i
(
x
)
,
μ
X
(
x
)
}
,
∀
i
μ_{\overline{P}X}(F_i)=sup_x\min\{μ_{F_i}(x),μ_X(x)\},\space \forall{i}
μPX(Fi)=supxmin{μFi(x),μX(x)}, ∀i
需要注意的是,尽管特征选择中的论域是有限的,但一般情况下并非如此,因此使用 s u p sup sup和 i n f inf inf。
i n f inf inf在这里的运算相当于取最小值, s u p sup sup在这里的运算相当于取最大值, X ∈ U X\in\mathbb{U} X∈U, X X X的意义是目标集合的特征。我们依次对式子进行分析以帮助理解这里的概念:
①:粗糙集理论对下近似集的定义为所有元素的目标属性符合 X X X的等价类的全部元素构成的类:
P ‾ X = { x ∣ [ x ] p ⊆ X } \underline{P}X=\{x|[x]_p\subseteq X\} PX={x∣[x]p⊆X}
回顾之后,看回当前公式,公式中的 m a x max max算子是衡量隶属度的主体, 1 − μ F i ( x ) 1-μ_{F_i}(x) 1−μFi(x)衡量了样本 x x x对等价类 F i F_i Fi的隶属度取反,而 μ X ( x ) μ_X(x) μX(x)衡量了 x x x样本对于目标样本 X X X的隶属度。这里说明,如果 x x x对于 F i F_i Fi的隶属度很低,那么它对于目标样本的隶属度不成为影响因素。而我们需要注意,每个等价类存在隶属度为1的元素, i n f inf inf巧妙控制了最后的取值。
②:粗糙集理论对上近似集的定义为存在元素的目标属性符合 X X X的等价类的全部元素构成的类:
P ‾ X = { x ∣ [ x ] p ∩ X ≠ ∅ } \overline{P}X=\{x|[x]_p\cap X \neq \empty \} PX={x∣[x]p∩X=∅}
看回当前公式, min \min min算子为衡量隶属度的主体,综合评价了样本 x x x对于等价类 F i F_i Fi和目标样本 X X X的隶属度,由于是 s u p sup sup控制最后的取值, F i F_i Fi对于上近似集的隶属度会取决于对于等价类隶属度和目标元素隶属度“双高”的样本。
然而,即使我们获取了模糊等价类的模糊近似隶属度,由于隶属度不具有传递性,我们不能清晰地定义一个目标集合上近似模糊集和下近似模糊集。在这里,我们定义对于每个样本 x x x的模糊下近似隶属度和模糊上近似隶属度:
μ P ‾ X ( x ) = sup F ∈ U / P m i n ( μ F ( x ) , inf y ∈ U max { 1 − μ F ( y ) , μ X ( y ) } ) μ_{\underline{P}X}(x)=\sup\limits_{F\in\mathbb{U}/P}min(μ_F(x),\inf\limits_{y\in\mathbb{U}}\max\{1-μ_F(y),μ_X(y)\}) μPX(x)=F∈U/Psupmin(μF(x),y∈Uinfmax{1−μF(y),μX(y)})
μ P ‾ X ( x ) = sup F ∈ U / P m i n ( μ F ( x ) , sup y ∈ U min { μ F ( y ) , μ X ( y ) } ) μ_{\overline{P}X}(x)=\sup\limits_{F\in\mathbb{U}/P}min(μ_F(x),\sup\limits_{y\in\mathbb{U}}\min\{μ_F(y),μ_X(y)\}) μPX(x)=F∈U/Psupmin(μF(x),y∈Usupmin{μF(y),μX(y)})
在上述公式中,变量 x , y x,y x,y均代表样本,相当于枚举。可以很容易观察出,公式的后半段与之前的公式大同小异,其意义是相通的。将公式后半段相似的算子看作等价类对于近似集的隶属度,同时 m i n min min算子加入了 μ F ( x ) μ_F(x) μF(x)对 F F F的隶属度,来衡量 x x x在 F F F中对于近似集的隶属度。最后 s u p sup sup保证是最优的情况。
模糊粗糙集数据降维
模糊粗糙集理论建立在模糊下近似概念的基础上,能够对包含实值特征的数据集进行属性约简。当我们定义了明确的决策属性时,约简的方法就和粗糙集理论的方法一致了。
传统粗糙集的正域被定义为下近似集的并集。根据扩展原理,属于模糊正域的对象
x
∈
U
x\in\mathbb{U}
x∈U的隶属度可以被定义为:
μ P O S P ( Q ) ( x ) = sup X ∈ U / Q μ P ‾ X ( x ) μ_{POS_P(Q)}(x)=\sup\limits_{X\in\mathbb{U}/Q}μ_{\underline{P}X}(x) μPOSP(Q)(x)=X∈U/QsupμPX(x)
其中 Q Q Q为决策属性, X X X为在论域 U \mathbb{U} U中被 Q Q Q划分的等价类。
使用模糊正区域的定义,新的Dependency Function可以定义如下:
γ P ′ ( Q ) = ∣ μ P O S P ( Q ) ( x ) ∣ ∣ U ∣ = ∑ x ∈ U μ P O S P ( Q ) ( x ) ∣ U ∣ γ^{'}_P(Q)=\frac{|μ_{POS_{P}(Q)}(x)|}{|\mathbb{U}|}=\frac{\sum_{x\in\mathbb{U}}μ_{POS_{P}(Q)}(x)}{|\mathbb{U}|} γP′(Q)=∣U∣∣μPOSP(Q)(x)∣=∣U∣∑x∈UμPOSP(Q)(x)
这里的函数值代表了整个数据集可识别出下近似集元素的比例。
当我们处理的决策属性为不可分割的属性集合时,需要将该集合当作一个属性进行处理:
假如 P = a , b , U / I N D ( { a } ) = { N a , Z a } , U / I N D ( { b } ) = { N b , Z b } P={a,b},\mathbb{U}/IND(\{a\})=\{N_a,Z_a\},\mathbb{U}/IND(\{b\})=\{N_b,Z_b\} P=a,b,U/IND({a})={Na,Za},U/IND({b})={Nb,Zb},那么:
U / P = { N a ∩ N b , N a ∩ Z b , Z a ∩ N b , Z a ∩ Z b } \mathbb{U}/P=\{N_a\cap N_b,N_a\cap Z_b,Z_a\cap N_b,Z_a\cap Z_b\} U/P={Na∩Nb,Na∩Zb,Za∩Nb,Za∩Zb}
模糊粗糙集快速约简
我们知道Dependency Function这个评价函数后,提出下面算法。
算法思路:每次一次加入最好的特征,直到再加入时函数的值不再增长,算法复杂度是
n
2
n^2
n2

例子太长可能不补充,给原文:
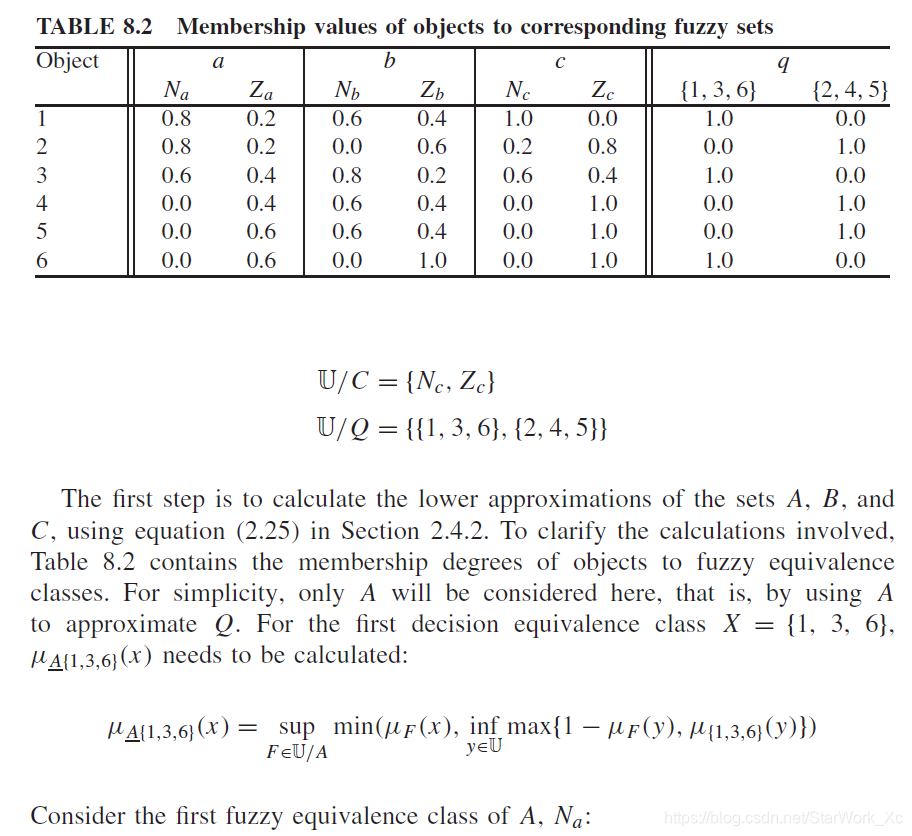


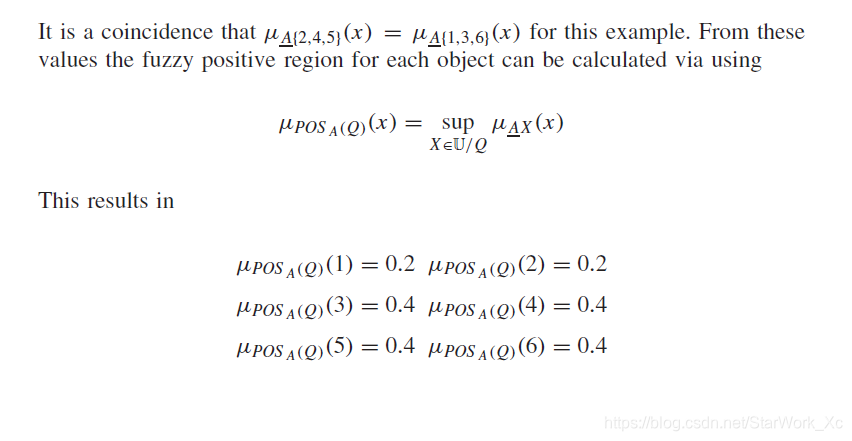






















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








