并查集是一种树型的数据结构,用于处理一些不相交集合(Disjoint Sets)的合并及查询问题。它的功能主要有:
1、找到某个节点的头节点
2、查询两个节点是否在同一个集合里
3、合并两个集合
具体算法为:
在给定的一个集合中,所有的节点都指向第一个节点,而第一个节点指向自身,查询是否位于同一集合,我们直接查询节点的父节点是否为同一个节点(该节点指向自身),合并两个集合时,我们将集合的父节点合并。这样就能轻松实现查询与合并。
并查集的数学模型是一组不相交的动态集合的集合S={A,B,C,...},它支持以下的运算:
(1)union(A,B):将集合A和B合并,其结果取名为A或B;
(2)find(x):找出包含元素x的集合,并返回该集合的名字。
/**
* 并查集
* @author Administrator
*
*/
public class UnionFindSet {
int num = 6; //顶点数
int[] parent = new int[num];
/**
* 初始化parent数组
* @param parent
*/
public void initialize(int parent[]) {
for (int i = 0; i < num; i++)
parent[i] = -1;
}
/**
* 合并两个节点,返回0表示合并失败,返回1表示合并成功
* @param x
* @param y
* @param parent
* @return
*/
public int union(int x, int y, int parent[]) {
int x_root = find(x, parent);
int y_root = find(y, parent);
if(x_root == y_root) { //如果根节点是同一个,则无需合并
return 0;
}else {
parent[x_root] = y_root; //合并:把x的父节点设为y
return 1;
}
}
/**
* 找到x的根节点
* @param x
* @param parent
* @return
*/
public int find(int x, int parent[]){
int x_root = x; //假设x的根节点是它本身
while(parent[x_root] != -1) { //如果x_root有父节点,则一层层往上找,直到找到顶层的父节点
x_root = parent[x_root];
}
return x_root;
}
}
图示:
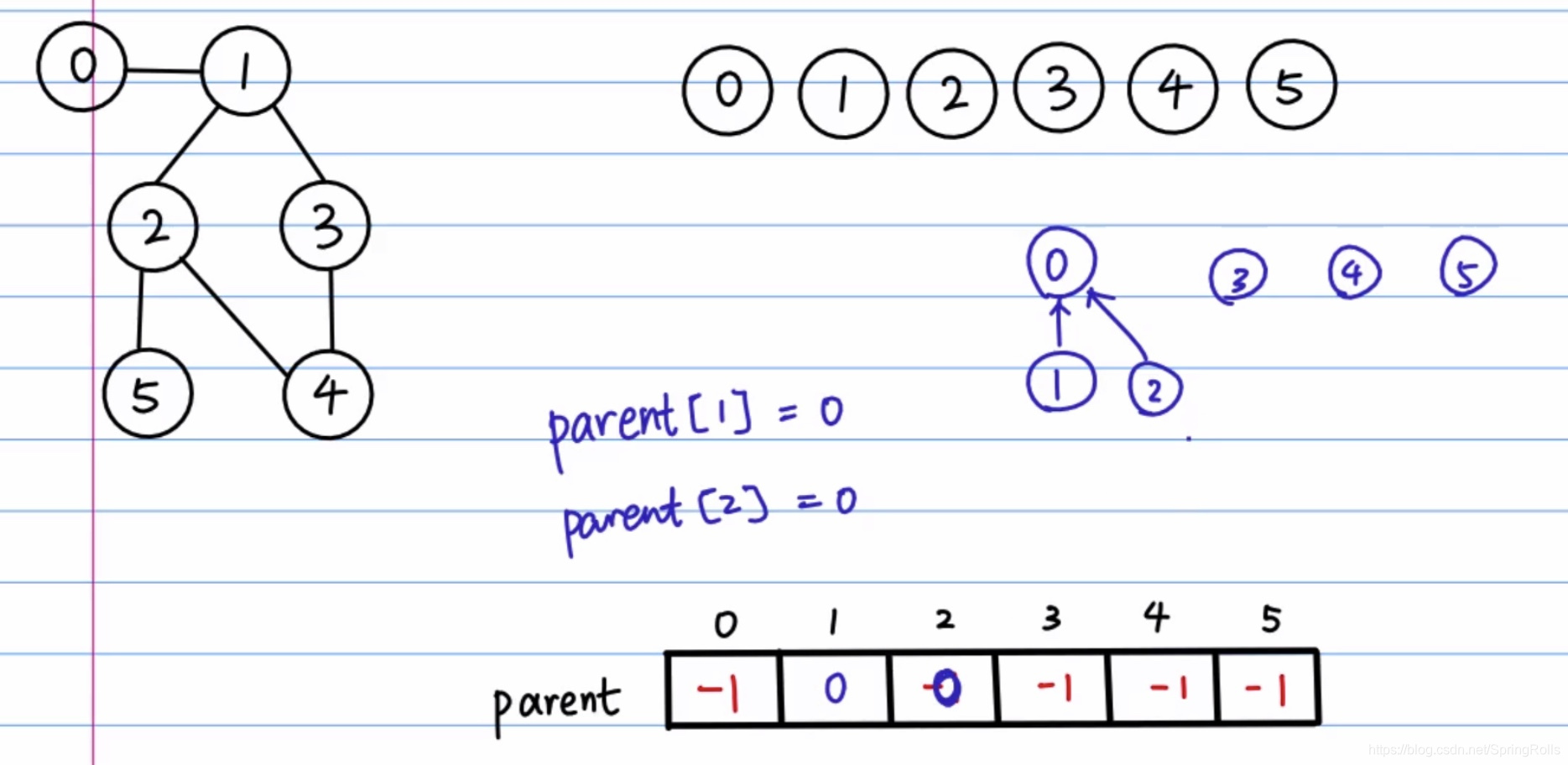





 本文深入解析并查集这一高效的数据结构,介绍其在处理不相交集合问题中的应用,包括查找节点头节点、判断两节点是否同属一集合以及集合合并操作。通过实例演示并查集的算法实现,帮助读者理解并查集的工作原理。
本文深入解析并查集这一高效的数据结构,介绍其在处理不相交集合问题中的应用,包括查找节点头节点、判断两节点是否同属一集合以及集合合并操作。通过实例演示并查集的算法实现,帮助读者理解并查集的工作原理。
















 1306
1306

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








