【面试题&LeetCode4】两个有序数组合并后的中位数

最新推荐文章于 2024-12-03 21:43:08 发布

原创

最新推荐文章于 2024-12-03 21:43:08 发布 · 1.2k 阅读

1 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #有序数组合并中位数 #分治 #二分查找

这篇博客探讨了如何在面试中优化两个有序数组合并后求中位数的问题，避免O(n)的时间复杂度，转而采用O(logn)的解决方案，利用二分查找和分治策略。博主将问题转化为TopK问题，并提供了相关代码实现，最终得出中位数为3.5。

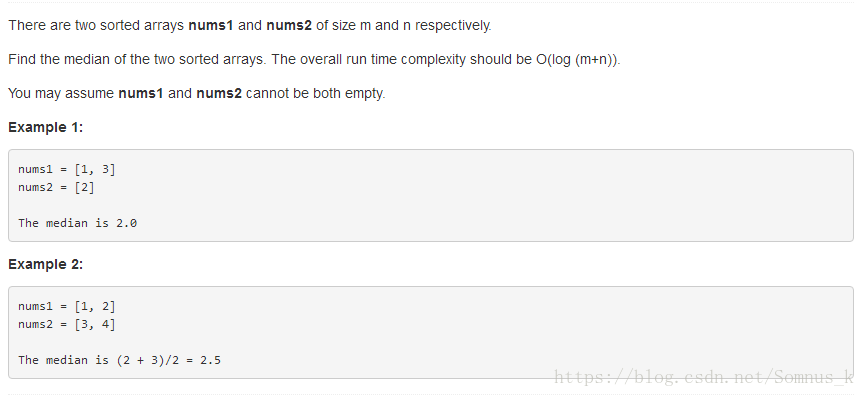
最简单的方法就是两个指针遍历两个数组，同时进行比较并计数，找到中位数，时间复杂度O(n)。

但是，这个方法并不是面试官想要的。于是会问，还有没有更快的方法，比O(n)更快的就只能想到O(logn)了，所以采用二分查找和分治算法来解决。

具体讲解参考：https://www.cnblogs.com/voidsky/p/5373982.html

将求中位数为题转化为TopK问题。

实现代码：

public class mid {

	public static void main(String[] args) {
		int[] num1 = {1,2,3};
		int[] num2 = {4,5,6};
		System.out.println(findMedianSortedArrays(num1,num2));
	}
	static double findMedianSortedArrays(int[] nums1, int[] nums2) {
        int n =nums1.length;
        int m = nums2.length;
        if(n > m)   //保证数组1一定最短
            return findMedianSortedArrays(nums2,nums1);
        int L1 = 0,L2 = 0,R1 = 0,R2 = 0,c1,c2,lo = 0, hi = 2*n;  //我们目前是虚拟加了'#'所以数组1是