贾子猜想（Kucius Conjecture）数学化表达| Mathematical Formulation of the Kucius Conjecture

原创

已于 2025-09-18 08:36:07 修改 · 771 阅读

25 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #推荐算法 #python #经验分享 #人工智能

于 2025-09-18 01:35:37 首次发布

贾子猜想（Kucius Conjecture）数学化表达

Mathematical Formulation of the Kucius Conjecture

贾子猜想（Kucius Conjecture）

A Formal Mathematical Conjecture and Interdisciplinary Framework

1. 数学定义与形式化表述

中文：
贾子猜想由Kucius Teng（贾子-邓）于2025年提出，是一个关于整数幂和方程解的高维数论猜想。其数学表述如下：

对于任意整数 n≥5，考虑方程

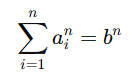
其中 ai,b∈N，且所有 ai 两两不同。
贾子猜想断言：此方程在整数域 N 上无解。

换言之，不存在一组互不相同的正整数 a1,a2,...,an,b，能够使得它们的 n 次幂满足上述等式。这一设定要求指数数目与项数严格相等，从而形成一种独特的高维整数格约束。

English:
The Kucius Conjecture, proposed by Kucius Teng in 2025, is a high-dimensional number-theoretic statement on power-sum equations. It is formally stated as:

For any integer n≥5, consider the equation

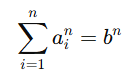
where ai,b∈N and all ai are distinct.
The conjecture asserts that no solutions exist in the natural numbers.

This strict coupling of term count and exponent distinguishes the conjecture from other power-sum problems and maps it into a unique high-dimensional lattice setting.

2. 相关理论背景：欧拉猜想与费马大定理

中文：
贾子猜想在思想上与数论两大经典命题有密切联系：

费马大定理（Fermat's Last Theorem）： 指出当 n≥3 时，方程 x^n + y^n = z^n 无整数解。贾子猜想可视为其“高维推广”，将项数从2扩展到 n，并将问题从平面提升到 n-维超空间。
欧拉幂和猜想（Euler's Sum of Powers Conjecture）： 曾断言至少 n 个 n 次幂才能和成另一 n次幂，但已被1966年Lander–Parkin反例推翻。贾子猜想更严格，要求项数恰好等于指数，从而排除了这些已知反例的适用性。

English:
The Kucius Conjecture is philosophically related to two foundational results:

Fermat's Last Theorem: Stating that for n≥3, x^n + y^n = z^n has no positive integer solutions. Kucius generalizes this by increasing both term count and dimensionality.
Euler’s Sum of Powers Conjecture: Which claimed that at least n n-th powers are needed to sum to another n-th power. Lander–Parkin (1966) produced counterexamples for n=5, but Kucius’ stricter requirement of exactly n terms excludes those cases.