LinkList

最新推荐文章于 2025-09-28 19:47:08 发布
原创 最新推荐文章于 2025-09-28 19:47:08 发布 · 786 阅读 · 3 ·
CC 4.0 BY-SA版权
博客大多是学习笔记，仅供自己总结回顾并无其他用途，并且大多都注明了出处，如有侵权，请告知，立即删除!

本文深入探讨了链式存储结构的定义、逻辑结构及其在单链表中的应用，包括结点定义、内部结构、插入与删除操作。同时，分析了链表与顺序表在时间复杂度、效率及工程开发中的优劣，提出了链表遍历的优化方法。

文章目录

1 线性表的链式存储结构

顺序存储结构的最大问题就是插入和删除时需要移动大量的元素，这个时候就需要链式存储结构的线性表出场了。

1.1 链式存储的定义

为了表示每个数据元素与其直接后继元素之间的逻辑关系，数据元素除了存储本身的信息外，还需要存储直接后继的信息。

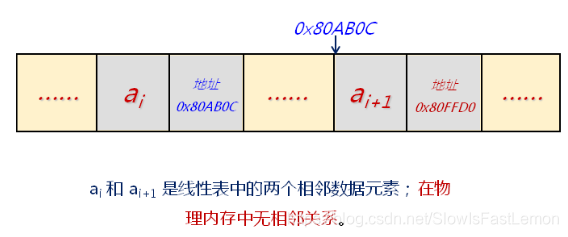
在这里插入图片描述

1.2 链式存储逻辑结构

基于链式存储结构的线性表中，每个结点都包含数据域和指针域。

  • 数据域：存储数据元素本身。
  • 指针域：存储相邻结点的地址。

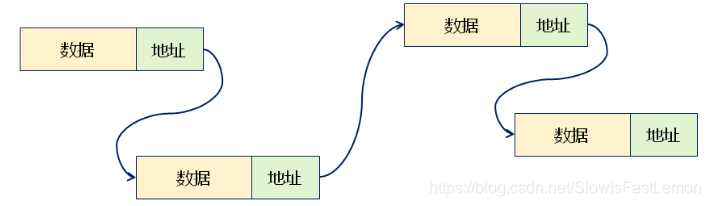
在这里插入图片描述

1.3 专业术语的统一

顺序表

  • 基于顺序存储结构的线性表

链表

  • 基于链式存储结构的线性表
    • 单链表：每个结点只包含直接后继的地址信息
    • 循环链表：单链表中的最后一个结点的直接后继为第一个结点
    • 双向链表：单链表中的结点包含直接前驱和直接后继的地址信息

1.4 链表中的基本概念

头结点： 链表中的辅助结点，包含指向第一个数据元素的指针。
数据结点： 链表中代表数据元素的结点，表现形式为：（数据元素，地址）。
尾结点： 链表中的最后一个数据结点，包含的地址信息为空。

1.5 单链表中的结点定义

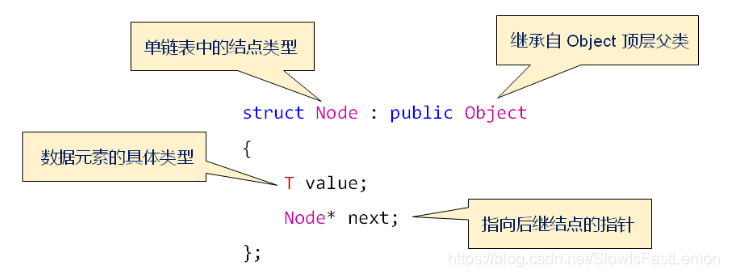
在这里插入图片描述

1.6 单链表的内部结构

在这里插入图片描述

头结点在单链表中的意义： 辅助数据元素的定位，方便插入和删除操作；因此，头结点不存储实际的数据元素。

1.7 在目标位置处插入数据元素

  1. 从头结点开始，通过current指针定位到目标位置。
  2. 从堆空间申请新的Node结点。
  3. 执行操作：
    node->value = e;
    node->next = current->next;
    current->next = node;

1.8 在目标位置处删除数据元素

  1. 从头结点开始，通过current指针定位到目标位置。
  2. 使用toDel指针指向需要删除的结点。
  3. 执行操作：
    toDel = current->next;
    current->next = toDel->next;
    delete toDel;

注意： 插入和删除操作一定要保证链表的完整性。

2 LinkList设计要点

  • 类模板，通过头结点访问后继结点。
  • 定义内部结点类型Node，用于描述数据域和指针域。
  • 实现线性表的关键操作（增，删，查，等）。

3 继承关系图和接口实现

继承关系图
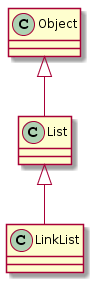
在这里插入图片描述

接口实现
在这里插入图片描述

4 代码实现

LinkList.h

#ifndef LINKLIST_H
#define LINKLIST_H

#include "List.h"
#include "Exception.h"

namespace LemonLib
{
template < typename T >
class LinkList : public List<T>
{
protected:
    struct Node : public Object
    {
        T value;
        Node* next;
    };

    mutable Node m_header;
    int m_length;

    Node* position(int index) const
    {
        Node* ret = &m_header;

        for (int i=0; i<index; i++)
        {
            ret = ret->next;
        }

        return ret;
    }
public:
    LinkList()
    {
        m_header.next = NULL;
        m_length = 0;
    }

    bool insert(int index, const T& e)
    {
        bool ret = (0 <= index) && (index <= m_length);

        if (ret)
        {
            Node* node = new Node();

            if (node != NULL)
            {
                Node* current = position(index);

                node->value = e;
                node->next = current->next;
                current->next = node;
                m_length++;
            }
            else
            {
                THROW_EXCEPTION(NoEnoughMemoryException, "No enough memory to inset element ...");
            }
        }

        return ret;
    }


    bool insert(const T& e)// 插入到尾部
    {
        return insert(m_length, e);
    }

    bool remove(int index)
    {
        bool ret = (0 <= index) && (index < m_length);

        if (ret)
        {
            Node* current = position(index);
            Node* toDel = current->next;

            current->next = toDel->next;
			
			m_length--;
            delete toDel;
        }

        return ret;
    }

    bool set(int index, const T& e)
    {
        bool ret = (0 <= index) && (index < m_length);

        if (ret)
        {
            position(index)->next->value = e;
        }

        return ret;
    }

    bool get(int index, T& e) const
    {
        bool ret = (0 <= index) && (index < m_length);

        if (ret)
        {
            e = position(index)->next->value;
        }

        return ret;

    }

    T get(int index) const
    {
        T ret;

        if (get(index, ret))
        {
            return ret;
        }
        else
        {
            THROW_EXCEPTION(InvalidParameterException, "Invalid parameter in get element...");
        }
    }
	int find(const T& e) const
    {
        int ret = -1;
        int index = 0;
        Node* current = m_header.next;

        while (current)
        {
            if (current->value == e)
            {
                ret = index;
                break;
            }
            else
            {
                index++;
                current = current->next;
            }
        }

        return ret;
    }

    int length() const
    {
        return m_length;
    }

    void clear()
    {
        while (m_header.next)
        {
            Node* toDel = m_header.next;
            m_header.next = toDel->next;
			
			m_length--;
            delete toDel;
        }
    }

    ~LinkList()
    {
        clear();
    }
};
}

#endif // LINKLIST_H

main.cpp

#include <iostream>
#include "Object.h"
#include "Exception.h"
#include "List.h"
#include "Seqlist.h"
#include "Staticlist.h"
#include "Dynamiclist.h"
#include "Staticarray.h"
#include "DynamicArray.h"
#include "Linklist.h"

using namespace std;
using namespace LemonLib;



int main()
{
    LinkList<int> list;

    for (int i=0; i<5; i++)
    {
        list.insert(i);

    }

    for (int i=0; i<list.length(); i++)
    {
        int val = 0;

        if (list.get(i, val))
        {
            cout << val << endl;
        }
    }
    cout << endl;

    list.remove(1);
    for (int i=0; i<list.length(); i++)
    {
        cout << list.get(i) << endl;
    }
    cout << endl;

    return 0;
}

5 头结点存在的隐患

在这里插入图片描述

如果写出如上的代码将会直接抛出异常，这显然是不合适的，因为这个时候仅仅创建了单链表类而没有创建有问题的Test类，因此我们需要对头结点进行优化。

优化后的代码如下：
LinkList.h

template < typename T >
class LinkList : public List<T>
{
protected:
    struct Node : public Object
    {
        T value;
        Node* next;
    };

    /* 注意：当前结构体必须继承自Object类，否则会导致和Node的内存布局不同，直接抛出异常 */
    mutable struct : public Object
    {
        char reserved[sizeof(T)];
        Node* next;
    }m_header;

    int m_length;

    Node* position(int index) const
    {
        Node* ret =  reinterpret_cast<Node*>(&m_header);

        for (int i=0; i<index; i++)
        {
            ret = ret->next;
        }

        return ret;
    }
public:
	// 和之前代码完全相同
};

6 顺序表和单链表分析

6.1 时间复杂度对比分析

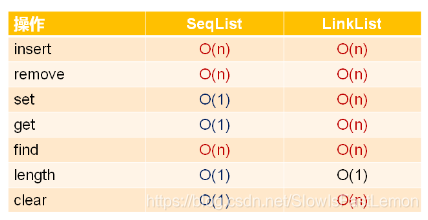
在这里插入图片描述

顺序表的整体时间复杂度比单链表要低，那么单链表还有使用价值吗？

6.2 效率深度分析

注意：在实际工程开发中，时间复杂度只是效率的一个参考指标。

对比点顺序表单链表
内置基础类型顺序表和链表效率不相上下顺序表和链表效率不相上下
自定义类型顺序表在效率上低于单链表顺序表在效率上低于单链表
插入和删除涉及大量数据对象的复制操作只涉及指针操作，效率与数据对象无关
数据访问随机访问，可直接定位数据对象顺序访问，必须从头访问数据，无法直接定位

工程开发中的实际选择：

  • 顺序表：数据元素类型相对简单，不涉及深拷贝；数据元素相对稳定，访问操作远多于插入和删除操作。
  • 单链表：数据元素类型相对复杂，复制操作相对耗时；数据元素不稳定，需要经常插入和删除，访问操作较少。

7 单链表的遍历与优化

7.1 当前遍历的问题

问题： 如何遍历单链表中每一个元素？

对于当前实现的链表来说，可以用如下的方式进行遍历：
在这里插入图片描述

可以看到通过上面的遍历方法我们不能以线性的时间复杂度完成单链表的遍历，目前遍历链表的时间复杂度是O(n2)，这显然是有改进的空间的。我们需要为单链表提供新的方法，以便实现在线性的时间内完成遍历。

7.2 优化的思路

设计思路

  • 在单链表内部定义一个游标（Node* m_current）
  • 遍历开始前将游标指向位置为0的数据元素
  • 获取游标指向的数据元素
  • 通过结点中的next指针移动游标

我们可以提供如下的一组函数，从而以线性的时间复杂度遍历链表。
在这里插入图片描述

遍历函数原型设计
在这里插入图片描述

注意：遍历相关的成员函数是相互依赖、相互配合的关系，一定要按照规则使用，否则将有可能出现错误！

7.3 代码实现

为了实现单链表类的扩展，我们对当前单链表内部再进行一次封装。
在这里插入图片描述

为了提高扩展性，我们对结点的申请和释放进行封装，这样我们就可以自己指定结点分配的空间。这里我们为静态单链表（StaticLinkList）的实现做准备，StaticLinkList与LinkList的不同仅在于链表结点在内存分配上的不同。因此，只需要将仅有不同封装在父类和子类的虚函数中。

LinkList.h

#ifndef LINKLIST_H
#define LINKLIST_H

#include "List.h"
#include "Exception.h"

namespace LemonLib
{
template < typename T >
class LinkList : public List<T>
{
protected:
    struct Node : public Object
    {
        T value;
        Node* next;
    };

    /* 注意：当前结构体必须继承自Object类，否则会导致和Node的内存布局不同，直接抛出异常 */
    mutable struct : public Object
    {
        char reserved[sizeof(T)];
        Node* next;
    }m_header;

    int m_length;
    Node* m_current;
    int m_step;

    Node* position(int index) const
    {
        Node* ret =  reinterpret_cast<Node*>(&m_header);

        for (int i=0; i<index; i++)
        {
            ret = ret->next;
        }

        return ret;
    }

    virtual Node* create()
    {
        return new Node();
    }

    virtual void destroy(Node* pn)
    {
        delete pn;
    }
public:
    LinkList()
    {
        m_header.next = NULL;
        m_length = 0;
        m_current = NULL;
        m_step = 0;
    }

    bool insert(int index, const T& e)
    {
        bool ret = (0 <= index) && (index <= m_length);

        if (ret)
        {
            Node* node = create();

            if (node != NULL)
            {
                Node* current = position(index);

                node->value = e;
                node->next = current->next;
                current->next = node;
                m_length++;
            }
            else
            {
                THROW_EXCEPTION(NoEnoughMemoryException, "No enough memory to inset element ...");
            }
        }

        return ret;
    }


    bool insert(const T& e)// 插入到尾部
    {
        return insert(m_length, e);
    }

    bool remove(int index)
    {
        bool ret = (0 <= index) && (index < m_length);

        if (ret)
        {
            Node* current = position(index);
            Node* toDel = current->next;

            current->next = toDel->next;

            if (m_current == toDel)
            {
                m_current = toDel->next;
            }

            m_length--;
            destroy(toDel);
        }

        return ret;
    }

    bool set(int index, const T& e)
    {
        bool ret = (0 <= index) && (index < m_length);

        if (ret)
        {
            position(index)->next->value = e;
        }

        return ret;
    }

    bool get(int index, T& e) const
    {
        bool ret = (0 <= index) && (index < m_length);

        if (ret)
        {
            e = position(index)->next->value;
        }

        return ret;

    }

   virtual T get(int index) const
    {
        T ret;

        if (get(index, ret))
        {
            return ret;
        }
        else
        {
            THROW_EXCEPTION(InvalidParameterException, "Invalid parameter in get element...");
        }
    }

    int find(const T& e) const
    {
        int ret = -1;
        int index = 0;
        Node* current = m_header.next;

        while (current)
        {
            if (current->value == e)
            {
                ret = index;
                break;
            }
            else
            {
                index++;
                current = current->next;
            }


        }

        return ret;
    }

    virtual bool move(int index, int step = 1)
    {
        bool ret = ((0 <= index) && (index < m_length) && (step > 0));

        if (ret)
        {
            m_current = position(index)->next;
            m_step = step;
        }

        return ret;
    }

    virtual bool end()
    {
        return (m_current == NULL);
    }

    virtual T current()
    {
        if (!end())
        {
            return m_current->value;
        }
        else
        {
            THROW_EXCEPTION(InvalidOperationException, "Invalid operation to get current value ...");
        }
    }

    virtual bool next()
    {
        int i = 0;
        while ((i < m_step) && (!end()))
        {
            m_current = m_current->next;
            i++;
        }

        return (i == m_step);
    }

    int length() const
    {
        return m_length;
    }

    void clear()
    {
        while (m_header.next)
        {
            Node* toDel = m_header.next;
            m_header.next = toDel->next;

            m_length--;
            destroy(toDel);
        }
    }

    ~LinkList()
    {
        clear();
    }
};
}

#endif // LINKLIST_H

main.cpp

#include <iostream>
#include "Object.h"
#include "Exception.h"
#include "List.h"
#include "Seqlist.h"
#include "Staticlist.h"
#include "Dynamiclist.h"
#include "Staticarray.h"
#include "DynamicArray.h"
#include "Linklist.h"

using namespace std;
using namespace LemonLib;


int main()
{
    LinkList<int> list;

    for (int i=0; i<5; i++)
    {
        list.insert(0, i);
    }


    for (list.move(0); !list.end(); list.next())
    {
        cout << list.current() << endl;
    }


    return 0;
}
数据结构（精讲）----链表Linklist----应用篇
Mumyi_的博客
01-22 1459
数据结构----链表（详解） 让你一文了解链表的各种操作
python中linklist理解
weixiyaya的博客
09-08 515
白露不漏身，寒露不漏脚。仲秋时节来到，注意保暖呀！学习python时留下的笔记，是在学完类之后，用类来模拟链表时的代码。为了重温知识，也是防止忘记链式结构。FIFO：全称First in, First out，先进先出。LIFO：全称Last in, First out，后进先出。 FIFO：先入先出队列，这是一种传统的按序执行方法，先进入的指令先完成并引退，之后才执行后面进入的指
单链表LinkList
12-31
使用数据结构中的方法，实现链式存储结构，达到节省空间的目的
数据结构_LinkList与链表
最新发布
2501_93103214的博客
09-28 2097
逻辑顺序实现：通过每个数据元素（通常称为 “节点”）中存储的引用（或指针） 来指示下一个（或上一个）节点的位置，从而将分散的节点串联起来，形成一个有序的逻辑序列。，效率比较低，因此ArrayList不适合做任意位置插入和删除比较多的场景。这意味着链表中的数据元素在计算机内存中不是紧密排列的，而是分散存储在不同的内存地址上。3．从堆上申请的空间，是按照一定的策略来分配的，两次申请的空间可能连续，也可能不连续。1．链式结构在逻辑上是连续的，但是在物理上不一定连续。2．现实中的结点一般都是从堆上申请出来的。
Java集合---LinkedList源码解析
weixin_34166847的博客
09-01 959
  一、源码解析1、 LinkedList类定义2、LinkedList数据结构原理3、私有属性4、构造方法5、元素添加add()及原理6、删除数据remove()7、数据获取get()8、数据复制clone()与toArray()9、遍历数据：Iterator()二、ListItr     一、源码解析     1、 LinkedList类定义。   public class ...
LinkList.cpp
01-22
该代码是单链表和其基本操作，如链表的创建与销毁；链表的插入、删除、查询等操作，查询可按元素查询也可指定位置；还有判断空表及表长等操作。
手写linklist demo
08-21
在本“手写linklist demo”中，我们将深入理解链表的原理，并通过编写代码来实现一个简单的链表示例。下面将详细讨论链表的基本概念、结构以及如何实现。 链表是一种线性数据结构，与数组不同，它不连续存储元素。...
LinkList.c
10-03
LinkList.c
精选资源
C#数据结构之单链表(LinkList)实例详解
01-20
本文实例讲述了C#数据结构之单链表(LinkList)实现方法。分享给大家供大家参考，具体如下： 这里我们来看下“单链表(LinkList)”。在上一篇《C#数据结构之顺序表(SeqList)实例详解》的最后，我们指出了：顺序表要求...
链表_LINKLIST
qeesung的专栏
06-05 3038
链表_LINKLIST 链表的结构 链表节点_LinkNode 链表节点连接 链表的基本操作 节点的插入_INSERTNODE 节点的删除_REMOVENODE 访问链表元素_VISITNODE 链表基本操作接口_INTERFACE 链表的编码实现 链表总结 本文中的所有代码都可以在这里: https://github.com/qeesung/algorithm/tree/master/chapt
Java重要类之LinkList类详解
热门推荐
生命奇迹泉的专栏
09-23 2万+
一.LinkList概述 LinkedList是一个继承于AbstractSequentialList的双向链表。它也可以被当作堆栈、队列或双端队列进行操作。 LinkedList 实现 List 接口，能进行队列操作。 LinkedList 实现Deque接口，即能将LinkedList当作双端队列使用。 LinkedList 实现了Cloneable接口，即覆盖了函数clone()，能克隆。
数据结构---单向链表，双向链表，单向环形链表
root1994的博客
07-09 5759
链表介绍 链表是以节点的方式来存储,是链式存储 每个节点包含 data 域， next 域:指向下一个节点. 如图:发现链表的各个节点不一定是连续存储. 链表分带头节点的链表和没有头节点的链表，根据实际的需求来确定 修改节点功能 思路(1) 先找到该节点，通过遍历，(2) temp.name = newHeroNode.name ; temp.nickname= newHeroNode.n...
linkList
weixin_39191862的博客
12-06 754
linkList
Linklist
yancuidandan的专栏
12-05 1090
#ifndef Linklist_H //避免重复包含Linklist.h头文件 #define Linklist_H template //定义单链表的结点 struct Node { DataType data; Node *next; }; template //类Li
评论
成就一亿技术人!
拼手气红包6.0元
还能输入1000个字符
 
红包 添加红包
表情包 插入表情
表情包 代码片
 条评论被折叠 查看
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值