SeqList

最新推荐文章于 2025-01-07 17:26:40 发布
原创 最新推荐文章于 2025-01-07 17:26:40 发布 · 5.5k 阅读 · 7 ·
CC 4.0 BY-SA版权
博客大多是学习笔记，仅供自己总结回顾并无其他用途，并且大多都注明了出处，如有侵权，请告知，立即删除!

本文深入探讨了线性表的顺序存储结构，包括定义、设计思路、关键操作的实现如元素获取、插入和删除，以及代码实现和效率分析。通过具体示例，读者将理解顺序存储结构的优缺点。

文章目录

1 线性表的顺序存储结构

1.1 顺序存储的定义

线性表的顺序存储结构，指的是用一段地址连续的存储单元依次存储线性表中的数据元素。

在这里插入图片描述

1.2 设计思路

可以用一维数组实现顺序存储结构。

  • 存储空间：T* m_array;
  • 当前长度：‘int m_length;’
template <typename T>
class SeqList : public List<T>
{
protected:
	T* m_array;
	int m_length;
	// ...
};

1.3 顺序存储结构的元素获取操作

（1）判断目标位置是否合法。
（2）将目标位置作为数据下标获取元素。

bool SeqList<T>::get(int index, T& e) const
{
	bool ret = ((0 <= index) && (index < m_length));
	
	if (ret)
	{
		e = m_array[index];
	} 

	return ret;
}

1.4 顺序存储结构的元素插入操作

（1）判断目标位置是否合法。
（2）将目标位置之后的所有元素后移一个位置。
（3）将新元素插入目标位置。
（4）线性表长度加1。

bool SeqList<T>::insert(int index, const T& e)
{
	bool ret = (0 <= index) && (index <= m_length);
	ret = ret && ((m_length + 1) <= capacity());

	if (ret)
	{
		for (int p=m_length-1; p>=index; p--)
		{
			m_array[p+1] = m_array[p];
		}
		
		m_array[index] = e;
		m_length++;
	}
}

1.5 顺序存储结构的元素删除操作

（1）判断目标位置是否合法。
（2）将目标位置后的所有元素前移一个位置。
（3）线性表长度减1。

bool SeqList<T>::remove(int index)
{
	bool ret = ((0 <= index) && (index < m_length));

	if (ret)
	{
		for (int p=index; i<m_length-1; i++)
		{
			m_array[p] = m_array[p+1];
		}
		
		m_length--;
	}

	return ret;
}

2 继承关系图和接口实现

SeqList实现要点

  • 抽象类模板，存储空间的位置和大小由子类完成
  • 实现顺序存储结构线性表的关键操作（增，删，查等）
  • 提供数组操作符，方便快速获取元素

顺序存储结构线性表继承关系图
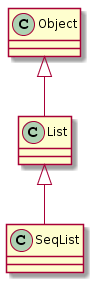
在这里插入图片描述

SeqList接口实现：

template < typename T >
class SeqList : public List<T>
{
protected:
    T* m_array;     // 顺序存储空间
    int m_length;   // 当前线性表长度

public:
    bool insert(int index, const T& e);	// O(n)
    bool insert(const T& e);			// O(1)
    bool remove(int index);				// O(n)
    bool set(int index, const T& e);	// O(1)
    bool get(int index, T& e) const;	// O(1)
    int find(const T& e) const;			// O(n)
    int length() const;					// O(1)
    void clear();						// O(1)

    // 顺序存储线性表的数组访问方式
    T& operator[](int index);			// O(1)
    T operator[](int index) const;		// O(1)
   
    // 顺序存储空间的容量
    virtual int capacity() const = 0;
};

3 代码实现

SeqList.h

#ifndef SEQLIST_H
#define SEQLIST_H

#include "Exception.h"

namespace  LemonLib
{

template < typename T >
class SeqList : public List<T>
{
protected:
    T* m_array;     // 顺序存储空间
    int m_length;   // 当前线性表长度

public:
    bool insert(int index, const T& e)
    {
        bool ret = ((0 <= index) && (index <= m_length));
        ret = ret && (m_length < capacity());

        if (ret)
        {
            for (int p=m_length-1; p>=index; p--)
            {
                m_array[p+1] = m_array[p];
            }

            m_array[index] = e;
            m_length++;
        }

        return ret;
    }

	bool insert(const T& e)
    {
        return insert(m_length, e);
    }
  
    bool remove(int index)
    {
        bool ret = ((0 <= index) && (index < m_length));

        if (ret)
        {
            for (int p=index; p<m_length-1; p++)
            {
                m_array[p] = m_array[p+1];
            }

            m_length--;
        }

        return ret;
    }

    bool set(int index, const T& e)
    {
        bool ret = ((0 <= index) && (index < m_length));

        if (ret)
        {
            m_array[index] = e;
        }

        return ret;
    }

    bool get(int index, T& e) const
    {
        bool ret = ((0 <= index) && (index < m_length));

        if (ret)
        {
            e = m_array[index];
        }

        return ret;
    }
	
	int find(const T& e) const
    {
        int ret = -1;

        for (int i=0; i<m_length; i++)
        {
            if (m_array[i] == e)
            {
                ret = i;
                break;
            }
        }

        return ret;
    }

    int length() const
    {
        return m_length;
    }

    void clear()
    {
        m_length = 0;
    }

    // 顺序存储线性表的数组访问方式
    T& operator[](int index)
    {
        bool ret = ((0 <= index) && (index < m_length));

        if (ret)
        {
            return m_array[index];
        }
        else
        {
            THROW_EXCEPTION(IndexOutOfBoundsException, "Param index is invalid...");
        }
    }

    T operator[](int index) const
    {
        return (const_cast<SeqList<T>&>(*this))[index];
    }


    // 顺序存储空间的容量
    virtual int capacity() const = 0;
};
}

#endif // SEQLIST_H

4 效率分析

在这里插入图片描述

5 思考

问题： 长度相同的两个SeqList，插入和删除操作的平均耗时是否相同？

元素的类型不同将导致插入和删除操作的平均耗时不同，比如一个数据类型为原生类型int，另一个数据类型为string，很明显两者的插入和删除操作的平均耗时有很大区别。

6 注意

  • 顺序存储线性表的插入和删除操作存在重大效率隐患（跟具体元素的类型有关）。
  • 线性表作为容器类，应当避免拷贝构造和拷贝赋值。
  • 顺序线性表可能被当成数组误用。
  • 工程开发中可以考虑使用数组类代替原生数组使用。
【数据结构入门】顺序表（SeqList）详解（初始化、增、删、查、改）
codewinter的博客
08-18 8万+
文章目录（1）线性表（2）顺序表1）什么是顺序表2）顺序表的定义2）顺序表的接口实现1、初始化顺序表2、销毁（释放）顺序表3、检查顺序表容量是否满了，好进行增容3、顺序表尾插4、顺序表尾删5、顺序表头插6、顺序表头删7、打印顺序表8、在顺序表中查找指定值9、在顺序表指定下标位置插入数据10、在顺序表中删除指定下标位置的数据11、查看顺序表中有效数据个数12、修改指定下标位置的数据 （1）线性表 线性表（linear list）是n个具有相同特性的数据元素的有限序列。 线性表是一种在实际中广泛使用的数据结
顺序表详解（SeqList）
kevin_blog
02-21 1816
通过代码讲解顺序表的原理及如何实现对顺序表的一系列操作。
seqlist.h头文件
12-27
seqlist.h头文件，包含了其中的源代码。很标准的哦。
List和SeqList
04-17
不仅自己编写的链表，同时可以调用STL中的list的模板。。是学习链表的基础知识。
SeqList作业rar
11-16
SeqList是一种常见的数据结构，它在计算机科学中扮演着重要角色，特别是在算法和数据结构的学习中。这个"SeqList作业rar"压缩包很显然是针对SeqList的一种编程作业或项目，可能包含了实现SeqList相关功能的代码。...
seqlist.cpp
最新发布
09-27
在计算机科学中，seqlist.cpp指的是一种特定的数据结构的实现文件，通常是在C++编程语言中对顺序表（Sequential List）的实现。顺序表是一种线性表的实现方式，它利用数组的连续存储空间来存储数据，使得元素在物理...
SeqList.java
12-12
SeqList.java
SeqList.cpp
09-12
invalid conversion from `void*&#39; to `SeqList*&#39; 说明你把void *指针付给SeqList*类型的指针了，是不是L=malloc(sizeof(SeqList));出问题了呢，malloc的正确用法是L=(SeqList *)malloc(sizeof(SeqList)); 希望能帮到...
SeqList.
feng_you000的专栏
06-15 821
基本SeqList:InitSeqList;PrintSeqList; PushBack; PopBack; PushFront;PopFront; Insert; Modified; removedm.
数据结构C++顺序表SeqList类
11-08
数据结构C++顺序表SeqList类的定义
Seqlist
狭路相逢勇者胜
06-24 938
#include #include //#include //about bool #define MAXSIZE 100#define ElemType inttypedef struct {  ElemType data[MAXSIZE];  int last; }Seqlist;Seqlist SeqlistInit() {  Seqlist L;  L.last=0;  return
seqlist
zmjames2000 Just record
02-21 413
#ifndef __SEQLIST_H__ #define __SEQLIST_H__ #include &lt;stdio.h&gt; #include &lt;stdlib.h&gt; typedef struct seqlist { int *data; int data_len; //相当于数组下标, 最后一位 int size; //记录顺序表分配的存储容量 }seqlist...
数据结构——顺序表（SeqList）
XLZ_44847的博客
11-03 863
顺序表，顾名思义就是顺序储存数据的数据管理方式。在物理层面来看，顺序表将表中的结点依次存放在计算机内存中一组地址连续的存储单元中。因为顺序表采用的是一段物理地址连续的储存单元一次存储数据元素，所以我们一般会采用数组的方式来存储。涉及到数组的存储，我们便会有两种方式，一种是静态的顺序表，即使用定长的数组来存储元素；而我们今天介绍的是另一种动态的顺序表，即采用动态开辟的数组进行数据的存储。
顺序表(sequence list)
个人独立博客http://www.acb0y.cn/
06-11 1623
/* Author: ACb0y Date: 2010-6-11 Description: sequen_list Version: 1.1 */ #include #define MAXSIZE 1 length = 0; } /* FUNCTION sequen_list_len
基于数组实现的顺序表(SeqList)
m0_74343467的博客
05-17 1083
顺序表介绍；基于数组实现的顺序表(SeqList)；自我实现顺序表(SeqList)
数据结构-顺序表(SeqList)
qq_38684512的博客
10-30 2284
顺序表 SeqListC实现C++实现 结构代表数据和数据之间的关系 1.同属一个集合 不允许元素重复 2.线性关系 一对一的关系 除了第一个之外 没有直接前驱最后一个没有直接后继 中间节点都有唯一前驱和唯一后继 3. 树形关系 一对多的关系 4. 图形关系 多对多的关系 1.逻辑存储 图像的样式 2.物理存储 内存中保存的样式 C实现 1.连续存储的线性聚集（别名 向量） 2.处第一个元素外，...
数据结构入门之顺序表（SeqList）
wuge041118的博客
01-07 671
顺序表的底层其实就是数组，那有了数组，为什么还要创建顺序呢？举个例子：假设我创建一个数组intarr[100]={1,2,3,4,5}，我想要插入删除或者查找某个数据就需要先查找数组中已有元素个数，再进行增删查，就使用循环，顺序表由此而生，。注：线性表是具有n个相同特性的数据元素的有限序列，主要从物理结构和逻辑结构两个方面有相同特性。在物理结构上不一定连续，即储存方式，如果储存方式是以数组的形式储存，则连续，如果以链式结构的方式储存则不连续；在逻辑结构上是连续的，也就是线性的。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值