/*邻接矩阵构造图,深度优先遍历和广度优先遍历
参考程杰的《大话数据结构》,但他的19年9月第23次印刷的
版本中存在代码的严重错误,本文对错误部分进行了修正
*/
/*错误的内容为scanf没有表明输入类型,以及多次调用
scanf存在回车键被录入的问题,所以需要将缓冲区的内容清空
*/
#include<stdio.h>
#include<stdlib.h>
typedef char VertexType;//顶点类型
typedef int EdgeType; //边的类型
#define MAXVEX 100 //最大顶点数
#define INFINITY 65535 //用65535来代表无穷
#define TRUE 1
#define FALSE 0
#define MAX 10
typedef int Boolean;//Boollean是布尔类型,其值是TRUE或者FALSE
Boolean visited[MAX];
typedef struct{
VertexType vexs[MAXVEX];//顶点表
EdgeType arc[MAXVEX][MAXVEX]; //邻接矩阵,可看作边表
int numVertexes,numEdges; //图中当前的顶点数和边数
}MGraph;
typedef int ElemType;
typedef struct LinkNode{
ElemType data;
struct LinkNode *next;
}LinkNode;
typedef struct Queue{
LinkNode *front,*rear;
}Queue;
void InitQueue(Queue &Q)
{
Q.front = Q.rear = (LinkNode*)malloc(sizeof(LinkNode));
Q.front->next = NULL;
}
bool IsEmpty(Queue Q)
{
if(Q.front==Q.rear)
{
return true;
}else
{
return false;
}
}
void EnQueue(Queue &Q,ElemType x)
{
LinkNode *s = (LinkNode *)malloc(sizeof(LinkNode));
s->data = x;
s->next = NULL;
Q.rear->next = s;
Q.rear = s;
}
bool DeQueue(Queue &Q,ElemType &x)
{
if(Q.front==Q.rear)
{
return false;
}
LinkNode *p = Q.front->next;
x = p->data;
Q.front->next = p->next;
if(Q.rear ==p)
{
Q.rear = Q.front;
}
free(p);
return true;
}
/*建立无项表的邻接矩阵表示*/
void CreateMGraph(MGraph *G)
{
int i,j,k,w;
printf("输入顶点数和边数\n");
scanf("%d,%d",&G->numVertexes,&G->numEdges);//输入顶点数和边数
printf("请输入顶点名称:");
fflush(stdin); //清除缓冲区,防止 回车重复读入
for( i = 0;i<G->numVertexes;i++)
{
scanf("%c",&G->vexs[i]); //顶点名称
fflush(stdin);//清除缓冲区,防止 回车重复读入
}
for(i = 0;i<G->numVertexes;i++)
{
for(j = 0;j<G->numVertexes;j++)
{
G->arc[i][j] = INFINITY;//邻接矩阵初始化
}
}
for(k = 0;k<G->numEdges;k++)
{
printf("输入边(vi,vj)上的下标i,和j和权w:\n");
scanf("%d,%d,%d",&i,&j,&w);//输入边(vi,vj)上的权w
G->arc[i][j] = w;//权重赋值
G->arc[i][j] = G->arc[j][i];//因为是无向图,矩阵对称
}
}
/*邻接矩阵的深度优先递归算法*/
void DFS(MGraph G,int i)
{
int j;
visited[i] = TRUE;
printf("%c ",G.vexs[i]);//打印顶点
for(j = 0;j<G.numVertexes;j++)
{
if(G.arc[i][j] ==1 &&!visited[j])
{
DFS(G,j);//对未访问的邻接顶点递归调用
}
}
}
/*邻接矩阵的深度遍历操作*/
void DFSTraverse(MGraph G)
{
int i;
for(i = 0;i < G.numVertexes; i++)
{
visited[i] = FALSE;//初始化visited数组,均未访问
}
for(i = 0;i < G.numVertexes; i++)
{
if(!visited[i])//对未访问的顶点调用DFS,如果为连通图,只会调用一次
{
DFS(G,i);
}
}
}
/*邻接矩阵的广度优先遍历算法*/
void BFSTraverse(MGraph G)
{
int i,j;
Queue Q;
for(i=0;i<G.numVertexes;i++)
{
visited[i] = FALSE;//初始化
}
InitQueue(Q);//辅助队列
for(i=0;i<G.numVertexes;i++)
{
if(!visited[i])
{
visited[i] = TRUE;//设置当前顶点访问过
printf("%c ",G.vexs[i]);//打印访问的结点
EnQueue(Q,i);//将其入队
while(!IsEmpty(Q))
{
DeQueue(Q,i);//将其出队
for(j=0;j<G.numVertexes;j++)
{
/*判断其他顶点与当前顶点是否有边并且未被访问过*/
if(G.arc[i][j] == 1 && !visited[j])
{
visited[j]=TRUE;//将找到的顶点标记为已访问
printf("%c ",G.vexs[j]);//打印改顶点
EnQueue(Q,j);//将其入队
}
}
}
}
}
}
int main()
{
MGraph G;
CreateMGraph(&G);
printf("深度优先遍历的结果为:\n");
DFSTraverse(G);
printf("\n");
printf("广度优先遍历的结果为:\n");
BFSTraverse(G);
return 0;
}
运行结果:
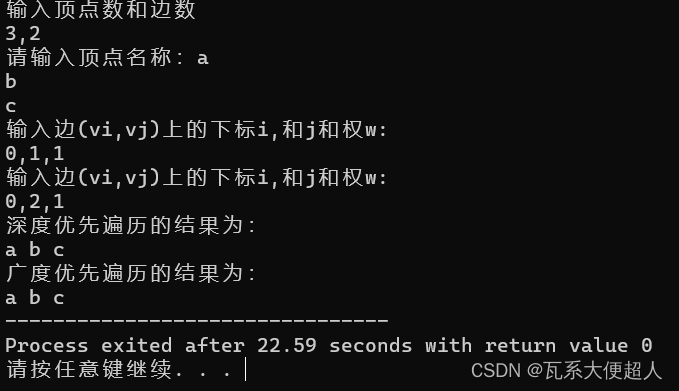




 该文提供了一个C语言实现的邻接矩阵图,包括了深度优先遍历(DFS)和广度优先遍历(BFS)的修正代码,解决了原书中存在的输入错误问题,如scanf的类型指定和回车键处理。程序首先创建无向图的邻接矩阵,然后进行DFS和BFS遍历,以遍历图中的所有顶点。
该文提供了一个C语言实现的邻接矩阵图,包括了深度优先遍历(DFS)和广度优先遍历(BFS)的修正代码,解决了原书中存在的输入错误问题,如scanf的类型指定和回车键处理。程序首先创建无向图的邻接矩阵,然后进行DFS和BFS遍历,以遍历图中的所有顶点。
















 1195
1195

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








