二叉树——基本概念

二叉树的概念

  树是一种非线性的数据结构，他有n(n>=0)个有限的结点组成的一个有层次关系的集合。之所以叫树，是因为这种数据结构看起来像是一个倒挂的树，根朝上，叶子朝下。特点就是每个结点有0个或多个结点，没有父结点的结点称为根结点，并且每一个非根结点有且只有一个父结点。二叉树就是其中的一种，二叉树中的每个结点只有两个子结点。

二叉树在实际中的优势

  在实际使用时会根据链表和有序数组等数据结构的不同优势进行选择。有序数组的优势在于二分查找，链表的优势在于数据项的插入和数据项的删除。但是在有序数组中插入数据就会很慢，同样在链表中查找数据项效率就很低。综合以上情况，二叉树可以利用链表和有序数组的优势，同时可以合并有序数组和链表的优势，二叉树也是一种常用的数据结构。

树中的名词：

结点的度：一个节点含有子树的个数称为这个结点的度。
树的度：一棵树中，最大的结点的度。
节点的层次：从根开始定义起，根为第1层，根的子节点为第2层，以此类推。
树的高度或深度：树中结点的最大层次。
兄弟节点：具有相同父节点的节点互称为兄弟节点。
二叉树（图）

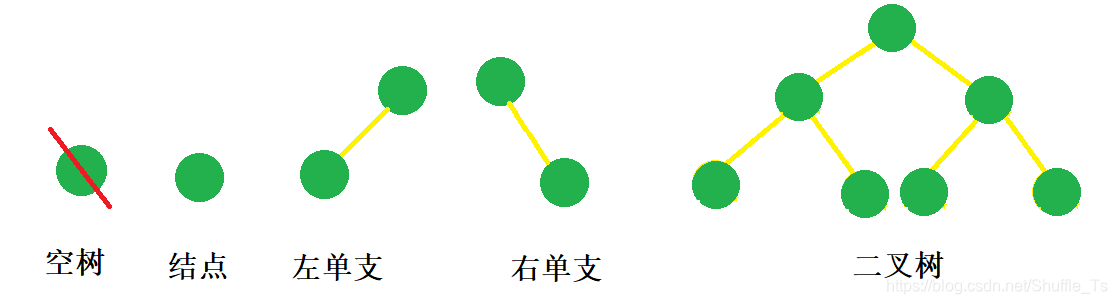
特殊的二叉树
  满二叉树：一个二叉树，如果每一层的系结点都达到了最大值，则这个二叉树就是满二叉树。如果一个二叉树的层数位K，且结点总数是(2^K)-1，这个二叉树就是满二叉树。
  完全二叉树：完全二叉树是效率很高的数据结构，如果一个二叉树的深度为n，除第n层外，其他各层（1~n-1）的节点数都达到最大个数，第h层所有节点都连续集中在最左边，这个二叉树就是完全二叉树。
二叉树的性质：
  若规定根节点的层数为1，则一个非空二叉树的第i层上最多有2^(i-1)个结点。(i>0)
  若规定只有根节点的深度为1，则深度为n的二叉树的最大结点数是(2^n)-1。(k>=0)
  对于任何一个二叉树，如果其叶子结点个数为n0,度为2的非叶子结点个数为n2，则有n0=n2+1。
  具有n个结点的完全二叉树深度k为log2（n+1）向上取整.
  对于具有n个结点的完全二叉树，如果按照从上至下从左至右的顺序对所有结点从0开始编号，则对于  序号为i的结点有：如果i>0,双亲序号为(i-1)/2；如果i=0，i为根节点编号，  没有父结点；如果2i+1<n，左孩子序列号为2i+1，否则没有左孩子；如果2i+2<n，右孩子序列号为2i+2，否则没有右孩子。
二叉树的存储
链式和顺序存储（堆）
二叉树链式存储实现

//创建新结点
BTreeNode* BuyBTreeNode(BTdataType data)
{
	BTreeNode* pNewNode = (BTreeNode*)malloc(sizeof(BTreeNode));
	if (pNewNode == NULL)
	{
		assert(0);
		return NULL;
	}
	pNewNode->data = data;
	pNewNode->left = NULL;
	pNewNode->right = NULL;

	return pNewNode;
}

//创建二叉树
BTreeNode* _CreatNode(vector<int> arr, size_t* index, BTdataType falg)
{

	BTreeNode* root = NULL;

	if (*index < arr.size() && arr[*index] != falg)
	{
		root = BuyBTreeNode(arr[*index]);
		(*index)++;
		root->left = _CreatNode(arr, index, falg);
		(*index)++;
		root->right = _CreatNode(arr, index, falg);
	}

	return root;
}


BTreeNode* CreatBTree(vector<int> arr, BTdataType falg)
{
	size_t index = 0;
	return _CreatNode(arr, &index, falg);
}


//前序遍历（递归）
void PreOrde(BTreeNode * root)
{
	if (root != NULL)
	{
		cout << root->data << " ";
		PreOrde(root->left);
		PreOrde(root->right);
	}
}
//前序遍历（非递归）
void PreOrde1(BTreeNode* root)
{
	//从最右结点开始压栈
	stack<BTreeNode*> buff;
	BTreeNode* cur = root;
	while (!buff.empty() || cur != NULL)
	{
		//向当前结点的左边一直延伸，直到NULL为止
		while (cur)
		{
			cout << cur->data << " ";
			buff.push(cur);
			cur = cur->left;
		}

		//到这里就说明当前结点为空了
		//如果栈中有数据，就说明不是二叉树的最后一个结点
		//就需要继续向后走
		if (!buff.empty())
		{
			BTreeNode* temp = buff.top();
			buff.pop();
			cur = temp->right;
		}
	}
}

//中序遍历（递归）
void InOrde(BTreeNode * root)
{
	if (root != NULL)
	{
		InOrde(root->left);
		cout << root->data << " ";
		InOrde(root->right);
	}
}
//中序遍历（非递归）
void InOrde1(BTreeNode* root)
{
	stack<BTreeNode*> buff;
	BTreeNode* cur = root;

	while (!buff.empty() || cur != NULL)
	{
		while (cur)
		{
			buff.push(cur);
			cur = cur->left;
		}

		if (!buff.empty())
		{
			BTreeNode* temp = buff.top();
			buff.pop();
			cout << temp->data << " ";
			cur = temp->right;
		}
	}
}

//后序遍历
void PostOrde(BTreeNode * root)
{
	if (root != NULL)
	{
		PostOrde(root->left);
		PostOrde(root->right);
		cout << root->data << " ";
	}
}
//后序遍历（非递归）
void PostOrde1(BTreeNode* root)
{
	stack<BTreeNode*> buff;
	BTreeNode* cur = root;
	//使用一个栈来同步当前结点的右子树是否已经处理完
	stack<bool> rf;
	
	while (!buff.empty() || cur != NULL)
	{
		while (cur)
		{
			buff.push(cur);
			cur = cur->left;
			//在判断栈中插入false，说明当前结点还有右子树没有遍历
			rf.push(false);
		}
		if (!buff.empty())
		{
			bool temp = rf.top();
			//如果是false，说明右子树还没有处理完
			//否则可以打印当前结点，右子树已经遍历完了
			if (temp)
			{
				cout << buff.top() << " ";
				buff.pop();
				rf.pop();
			}
			else
			{
				rf.pop();
				rf.push(true);
				cur = buff.top();
			}
		}
	}
}


//获取当前结点的左孩子
BTreeNode* LeftChild(BTreeNode* root)
{
	return root->left;
}
//获取当前结点的右孩子
BTreeNode* RightChild(BTreeNode* root)
{
	return root->right;
}

//销毁树
void DestoryBTree(BTreeNode** root)
{
	assert(root);
	if (*root)
	{
		DestoryBTree(&(*root)->left);
		DestoryBTree(&(*root)->right);
		free((*root));
		*root = NULL;
	}
}

//树中结点的个数
int BTreeSize(BTreeNode* root)
{
	if (root == NULL)
		return 0;
	else
		return BTreeSize(root->left) + BTreeSize(root->right) + 1;
}

//树中叶子结点的个数
int BTreeLeafSize(BTreeNode* root)
{
	if (root == NULL)
		return 0;

	if (root->left == NULL && root->right == NULL)
		return 1;

	return BTreeLeafSize(root->left) + BTreeLeafSize(root->right);
}

//树的高度
int BTreeHeight(BTreeNode* root)
{
	if (root == NULL)
		return 0;
	else
	{
		return max(BTreeHeight(root->left), BTreeHeight(root->right)) + 1;
	}
}

//在树中查找
BTreeNode* BTreeFind(BTreeNode* root, BTdataType x)
{
	if (root = NULL)
		return NULL;
	else if (root->data == x)
		return root;
	BTreeNode* ret = BTreeFind(root->left, x);
	if (ret != NULL)
	{
		return ret;
	}
	else
		return BTreeFind(root->right, x);

}

//树的层序遍历
void BinaryTreeLeveOrder(BTreeNode* root)
{
	if (root == NULL)
		return;
	queue<BTreeNode*> s;
	s.push(root);
	while (!s.empty())
	{
		BTreeNode* tmp = s.front();
		s.pop();
		cout << tmp->data << " ";
		if (tmp->left != NULL)
			s.push(tmp->left);
		if (tmp->right != NULL)
			s.push(tmp->right);
	}
}

//树的层数
int BTreeLevelKSize(BTreeNode* root, int k)
{
	if (root == NULL || k <= 0)
		return 0;
	if (k == 1)
		return 1;

	return BTreeLevelKSize(root, k - 1) + BTreeLevelKSize(root, k - 1);
}