class Solution {
public :
int specialArray ( vector< int > & nums) {
sort ( nums. begin ( ) , nums. end ( ) ) ;
int n = nums. size ( ) ;
if ( nums[ 0 ] >= n) return n;
for ( int i = 0 ; i < n - 1 ; i++ ) {
if ( nums[ i] < n - i - 1 && nums[ i + 1 ] >= n - i - 1 ) return n - i - 1 ;
}
if ( nums[ n - 1 ] < 0 ) return 0 ;
return - 1 ;
}
} ;
class Solution {
public :
vector< int > shortestAlternatingPaths ( int n, vector< vector< int >> & redEdges, vector< vector< int >> & blueEdges) {
vector< int > ans ( n, - 1 ) ;
ans[ 0 ] = 0 ;
map< int , vector< int >> red;
map< int , vector< int >> blue;
for ( const auto & arr : redEdges) {
red[ arr[ 0 ] ] . push_back ( arr[ 1 ] ) ;
}
for ( const auto & arr : blueEdges) {
blue[ arr[ 0 ] ] . push_back ( arr[ 1 ] ) ;
}
set< pair< int , bool >> mySet;
queue< pair< int , bool >> myQueue;
for ( auto i : red[ 0 ] ) {
myQueue. push ( make_pair ( i, true ) ) ;
mySet. emplace ( make_pair ( i, true ) ) ;
}
for ( auto i : blue[ 0 ] ) {
myQueue. push ( make_pair ( i, false ) ) ;
mySet. emplace ( make_pair ( i, false ) ) ;
}
int len = 1 ;
while ( ! myQueue. empty ( ) ) {
int sz = myQueue. size ( ) ;
while ( sz-- ) {
auto [ to, isRed] = myQueue. front ( ) ;
myQueue. pop ( ) ;
if ( ans[ to] == - 1 ) {
ans[ to] = len;
}
vector< int > nextNodes;
if ( isRed) nextNodes = blue[ to] ;
else nextNodes = red[ to] ;
for ( auto nex : nextNodes) {
if ( ! mySet. count ( make_pair ( nex, ! isRed) ) ) {
mySet. emplace ( make_pair ( nex, ! isRed) ) ;
myQueue. push ( make_pair ( nex, ! isRed) ) ;
}
}
}
len++ ;
}
return ans;
}
} ;
class Solution {
public :
int minReorder ( int n, vector< vector< int >> & connections) {
vector< vector< int >> conn_idx ( n, vector < int > ( ) ) ;
for ( int i = 0 ; i < connections. size ( ) ; i++ ) {
conn_idx[ connections[ i] [ 0 ] ] . push_back ( i) ;
conn_idx[ connections[ i] [ 1 ] ] . push_back ( i) ;
}
vector< bool > vi ( connections. size ( ) , false ) ;
int ans = 0 ;
queue< int > que;
que. push ( 0 ) ;
while ( ! que. empty ( ) ) {
auto q = que. front ( ) ;
que. pop ( ) ;
for ( auto idx : conn_idx[ q] ) {
if ( vi[ idx] ) continue ;
vi[ idx] = true ;
int a = connections[ idx] [ 0 ] ;
int b = connections[ idx] [ 1 ] ;
ans += ( a == q) ;
a = ( a == q) ? b : a;
que. push ( a) ;
}
}
return ans;
}
} ;
class Solution {
public :
int shortestPathLength ( vector< vector< int >> & graph) {
int n = graph. size ( ) ;
if ( n == 1 ) return 0 ;
queue< pair< int , int >> myQueue;
for ( int i = 0 ; i < n; i++ ) {
myQueue. push ( { i, 1 << i} ) ;
}
int len = 0 ;
set< pair< int , int >> visited;
while ( ! myQueue. empty ( ) ) {
int sz = myQueue. size ( ) ;
while ( sz-- ) {
auto [ i, mask] = myQueue. front ( ) ;
myQueue. pop ( ) ;
if ( mask == ( 1 << n) - 1 ) {
return len;
}
if ( visited. count ( make_pair ( i, mask) ) ) continue ;
visited. emplace ( make_pair ( i, mask) ) ;
for ( auto j : graph[ i] ) {
int tmp = mask | ( 1 << j) ;
myQueue. push ( { j, tmp} ) ;
}
}
len++ ;
}
return - 1 ;
}
} ;
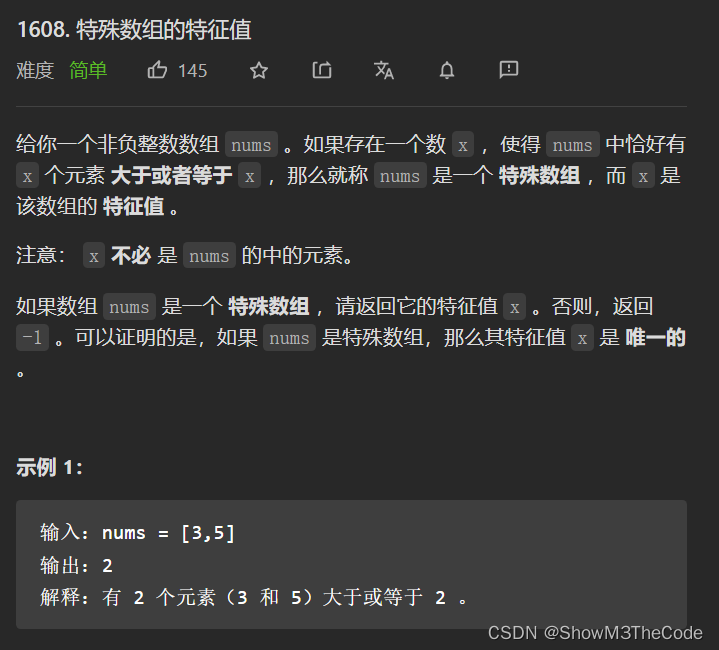
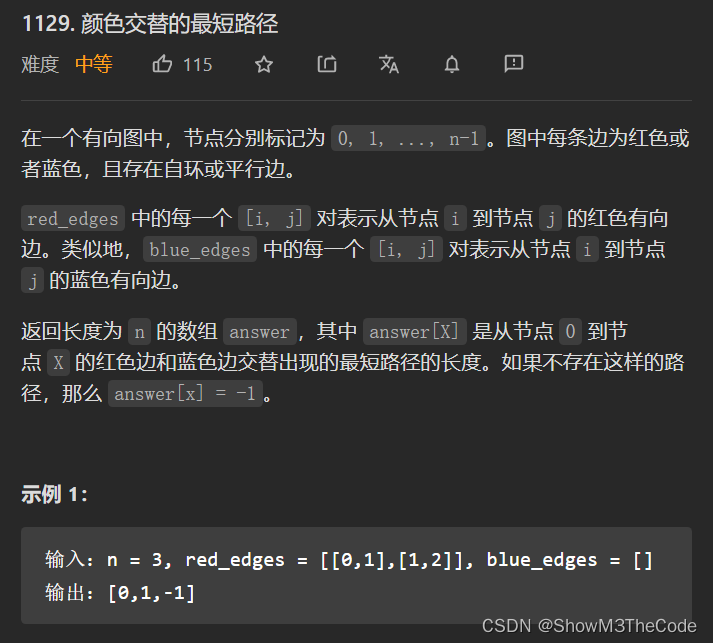
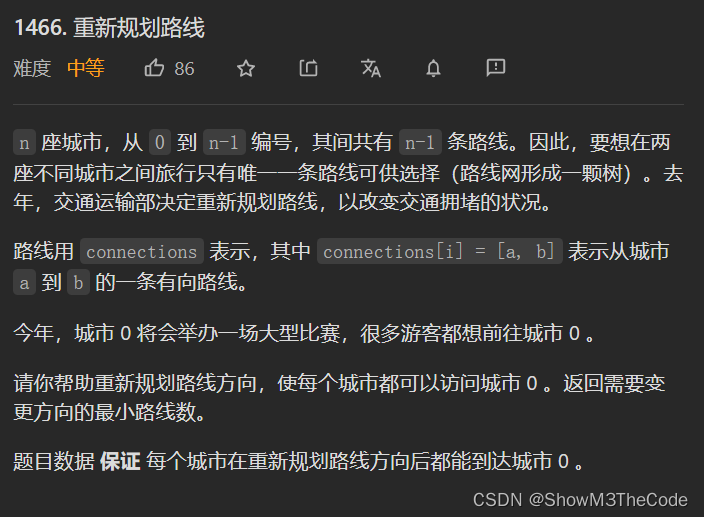
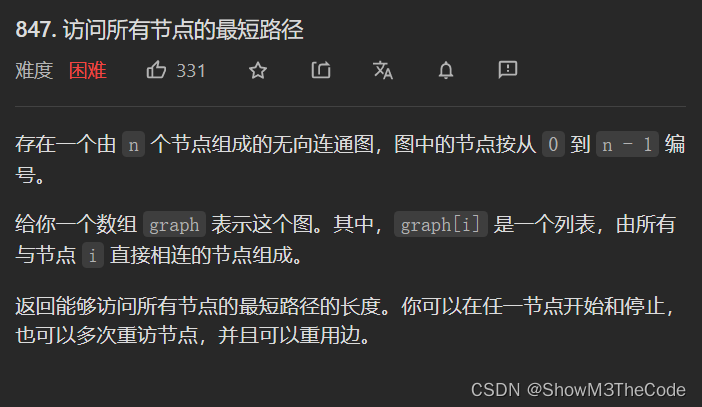





 这篇博客包含四个代码实现,分别解决特殊数组的特征值问题、颜色交替的最短路径、重新规划路线以及访问所有节点的最短路径。通过排序、队列、图遍历等算法,找到最优解并返回结果。
这篇博客包含四个代码实现,分别解决特殊数组的特征值问题、颜色交替的最短路径、重新规划路线以及访问所有节点的最短路径。通过排序、队列、图遍历等算法,找到最优解并返回结果。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








