聚类的指标
聚类分析中常用的评估指标包括轮廓系数(Silhouette Score)、Calinski-Harabasz指数、Davies-Bouldin指数等。这些指标用于评估聚类结果的质量,帮助选择最佳的聚类算法和参数。
聚类常见算法
常见的聚类算法包括KMeans聚类、DBSCAN聚类和层次聚类。这些算法各有特点,适用于不同的数据集和场景。
三种算法对应的流程
KMeans聚类:首先随机选择K个中心点,然后迭代更新中心点,直到收敛。最终将每个样本分配到最近的中心点。
DBSCAN聚类:通过定义核心点和密度可达的关系,将样本划分为不同的簇。该算法不需要预先指定簇的数量。
层次聚类:通过构建树状结构,逐层合并或分裂簇。层次聚类可以是凝聚的(自底向上)或分裂的(自顶向下)。
实际在论文中聚类的策略
在实际研究中,聚类的策略不一定是针对所有特征,可以选择其中几个可解释的特征进行聚类。这样得到的聚类结果在后续解释时更加符合逻辑。
聚类的流程
标准化数据:对数据进行标准化处理,确保不同特征的量纲一致。
选择合适的算法,根据评估指标调参:KMeans和层次聚类的参数是K值,选择合适的K值后指标确定。DBSCAN的参数是eps和min_samples,选择合适的参数后出现K和评估指标。层次聚类的linkage准则等也需要仔细调优。
将聚类后的特征添加到原数据中:将聚类结果作为新特征添加到原数据中,便于后续分析。
原则t-SNE或者PCA进行2D或3D可视化:使用t-SNE或PCA方法将高维数据降维至2D或3D,进行可视化展示。
作业:对心脏病数据集进行聚类
对心脏病数据集进行聚类分析,可以按照上述流程进行。首先对数据进行标准化处理,然后选择合适的聚类算法和参数,最后将聚类结果添加到原数据中,并进行可视化展示。
首先在进行聚类之前首先要对数据进行标准化处理
from sklearn.cluster import KMeans, DBSCAN, AgglomerativeClustering
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
scaler = StandardScaler()
x_scaled = scaler.fit_transform(x)确定K值范围,看聚类图,看转折点
from sklearn.metrics import silhouette_score, calinski_harabasz_score, davies_bouldin_score
k_range = range(2, 11) # 测试 k 从 2 到 10
inertia_values = []
silhouette_scores = []
ch_scores = []
db_scores = []
for k in k_range:
kmeans = KMeans(n_clusters=k, random_state=42) #n_cluster是一个参数,用于指定K-均值算法中的簇的数量。模型实例化
kmeans_labels = kmeans.fit_predict(x_scaled)#根据输入的数据来训练K-均值模型,返回每个数据点所属的簇标签。
inertia_values.append(kmeans.inertia_) # 惯性(肘部法则)将惯性值储存在惯性值列表垢面
silhouette = silhouette_score(x_scaled, kmeans_labels) # 计算轮廓系数,X_scaled是标准化后的特征数据,kmeans_labels是X_scaled每个数据点所属聚类结果的标签
silhouette_scores.append(silhouette)
ch = calinski_harabasz_score(x_scaled, kmeans_labels) # CH 指数
ch_scores.append(ch)
db = davies_bouldin_score(x_scaled, kmeans_labels) # DB 指数
db_scores.append(db)
print(f"k={k}, 惯性: {kmeans.inertia_:.2f}, 轮廓系数: {silhouette:.3f}, CH 指数: {ch:.2f}, DB 指数: {db:.3f}")
# 绘制评估指标图
plt.figure(figsize=(15, 10))
# 肘部法则图(Inertia)
plt.subplot(2, 2, 1)#subplot是创建子图的函数,2行2列,第1个图
plt.plot(k_range, inertia_values, marker='o')#plt.plot是绘制折线图的函数,k_range是x轴数据,inertia_values是y轴数据,marker='o'是折线图中的标记点
plt.title('肘部法则确定最优聚类数 k(惯性,越小越好)')
plt.xlabel('聚类数 (k)')
plt.ylabel('惯性')
plt.grid(True)
# 轮廓系数图
plt.subplot(2, 2, 2)
plt.plot(k_range, silhouette_scores, marker='o', color='orange')
plt.title('轮廓系数确定最优聚类数 k(越大越好)')
plt.xlabel('聚类数 (k)')
plt.ylabel('轮廓系数')
plt.grid(True)
# CH 指数图
plt.subplot(2, 2, 3)
plt.plot(k_range, ch_scores, marker='o', color='green')
plt.title('Calinski-Harabasz 指数确定最优聚类数 k(越大越好)')
plt.xlabel('聚类数 (k)')
plt.ylabel('CH 指数')
plt.grid(True)
# DB 指数图
plt.subplot(2, 2, 4)
plt.plot(k_range, db_scores, marker='o', color='red')
plt.title('Davies-Bouldin 指数确定最优聚类数 k(越小越好)')
plt.xlabel('聚类数 (k)')
plt.ylabel('DB 指数')
plt.grid(True)
plt.tight_layout()
plt.show()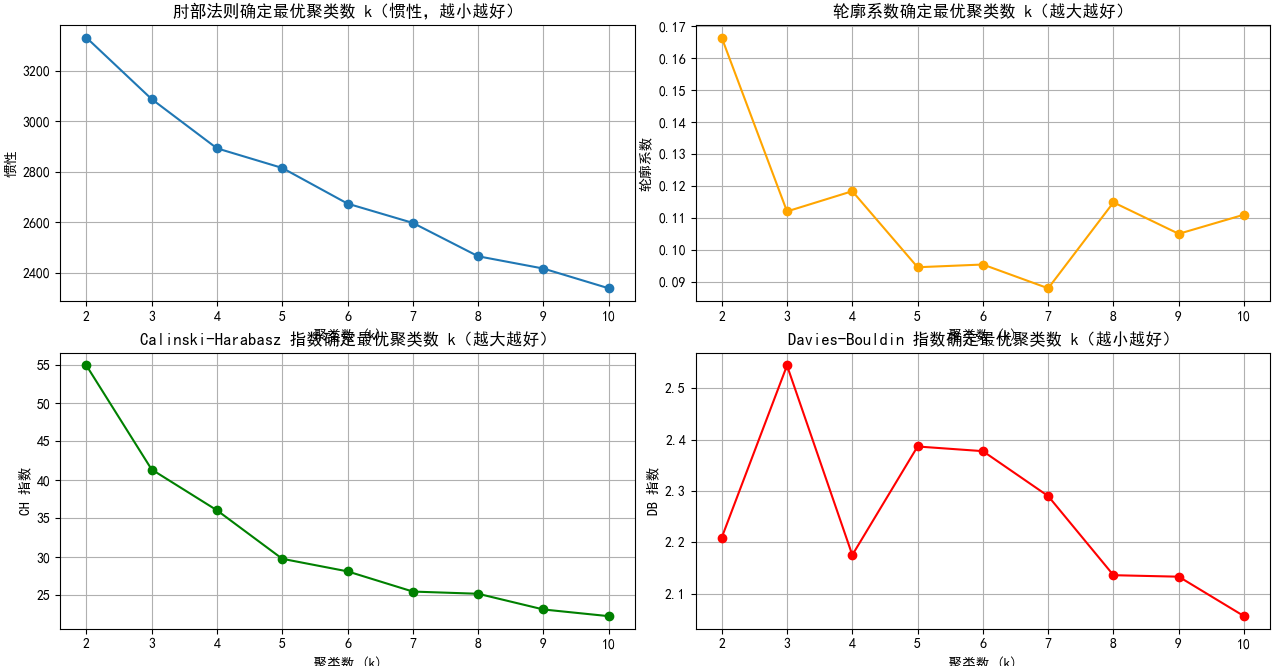
肘部法则图: 找下降速率变慢的拐点,这里都差不多
轮廓系数图:找局部最高点
CH指数图: 找局部最高点
DB指数图:找局部最低点
综合比较,4和8差不太多,我选4
然后对选择的k值进行聚类,pca降维,并将聚类结果可视化。
selected_k = 4
# 使用选择的 k 值进行 KMeans 聚类
kmeans = KMeans(n_clusters=selected_k, random_state=42)
kmeans_labels = kmeans.fit_predict(x_scaled)
x['KMeans_Cluster'] = kmeans_labels
# 使用 PCA 降维到 2D 进行可视化
pca = PCA(n_components=2)
x_pca = pca.fit_transform(x_scaled)
# KMeans 聚类结果可视化
plt.figure(figsize=(6, 5))
sns.scatterplot(x=x_pca[:, 0], y=x_pca[:, 1], hue=kmeans_labels, palette='viridis')
plt.title(f'KMeans Clustering with k={selected_k} (PCA Visualization)')
plt.xlabel('PCA Component 1')
plt.ylabel('PCA Component 2')
plt.show()
# 打印 KMeans 聚类标签的前几行
print(f"KMeans Cluster labels (k={selected_k}) added to X:")
print(x[['KMeans_Cluster']].value_counts())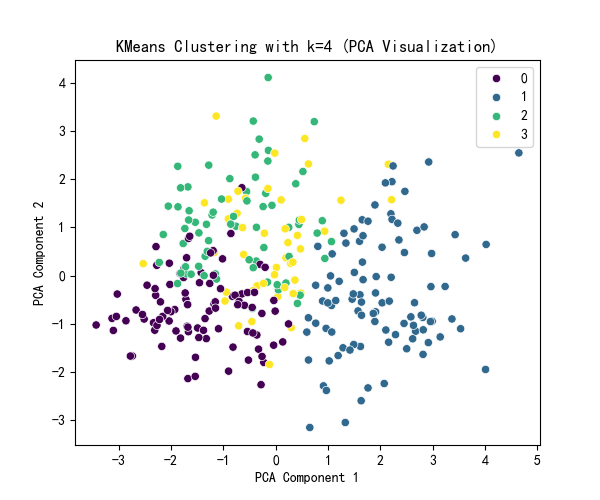
DBSCAN聚类
首先,我增加了一部,为了确定eps的取值范围
import numpy as np
from scipy.spatial import distance_matrix
# 生成示例数据
x_data = np.array(x_scaled)
# 计算所有点之间的距离矩阵
dist_matrix = distance_matrix(x_data, x_data)
# 找到每个点的最近邻距离(排除自身)
nearest_distances = np.sort(dist_matrix)[:, 1]
print("最近邻距离:")
print(nearest_distances)
# 对最近邻距离值进行排序
sorted_distances = np.sort(nearest_distances)
# 绘制曲线
import matplotlib.pyplot as plt
plt.figure(figsize=(10, 6))
plt.plot(sorted_distances)
plt.title('排序后的最近邻距离曲线')
plt.xlabel('数据点索引')
plt.ylabel('最近邻距离')
plt.grid(True)
plt.show()通过最近邻距离排序所获得的曲线来确定
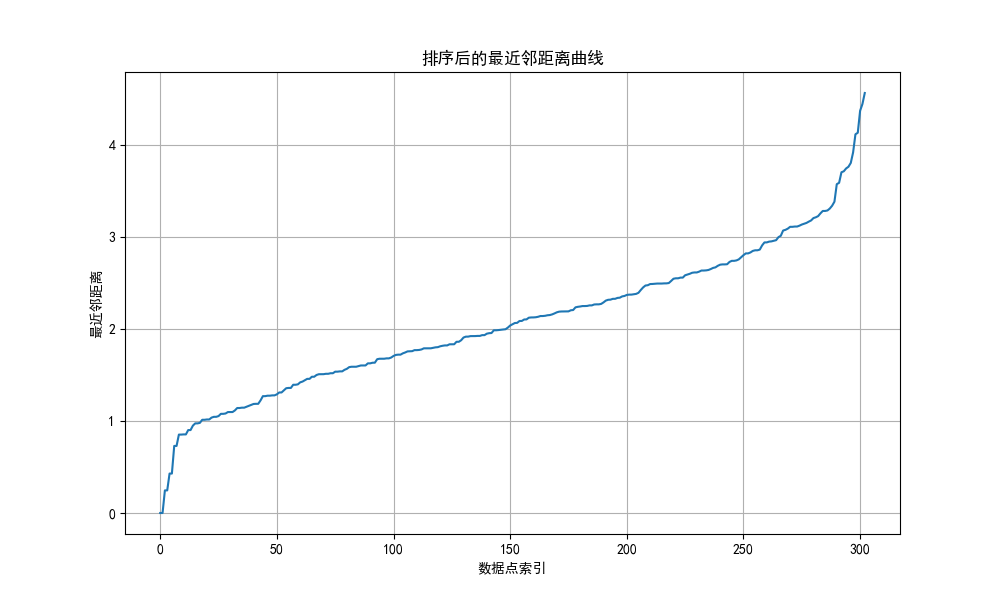
也就是两个斜率变化较大的点为取值范围
rom sklearn.metrics import silhouette_score, calinski_harabasz_score, davies_bouldin_score
eps_range = np.arange(0.8,3.5 , 0.5)
min_samples_range = range(3, 8)
results = []
for eps in eps_range:
for min_samples in min_samples_range:
dbscan = DBSCAN(eps=eps, min_samples=min_samples)
dbscan_labels = dbscan.fit_predict(x_scaled)
# 计算簇的数量(排除噪声点 -1)
n_clusters = len(np.unique(dbscan_labels)) - (1 if -1 in dbscan_labels else 0)
# 计算噪声点数量
n_noise = list(dbscan_labels).count(-1)
# 只有当簇数量大于 1 且有有效簇时才计算评估指标
if n_clusters > 1:
# 排除噪声点后计算评估指标
mask = dbscan_labels != -1
if mask.sum() > 0: # 确保有非噪声点
silhouette = silhouette_score(x_scaled[mask], dbscan_labels[mask])
ch = calinski_harabasz_score(x_scaled[mask], dbscan_labels[mask])
db = davies_bouldin_score(x_scaled[mask], dbscan_labels[mask])
results.append({
'eps': eps,
'min_samples': min_samples,
'n_clusters': n_clusters,
'n_noise': n_noise,
'silhouette': silhouette,
'ch_score': ch,
'db_score': db
})
print(f"eps={eps:.1f}, min_samples={min_samples}, 簇数: {n_clusters}, 噪声点: {n_noise}, "
f"轮廓系数: {silhouette:.3f}, CH 指数: {ch:.2f}, DB 指数: {db:.3f}")
else:
print(f"eps={eps:.1f}, min_samples={min_samples}, 簇数: {n_clusters}, 噪声点: {n_noise}, 无法计算评估指标")
# 将结果转为 DataFrame 以便可视化和选择参数
results_df = pd.DataFrame(results)
# 绘制评估指标图,增加点论文中的工作量
plt.figure(figsize=(15, 10))
# 轮廓系数图
plt.subplot(2, 2, 1)
for min_samples in min_samples_range:
subset = results_df[results_df['min_samples'] == min_samples] #
plt.plot(subset['eps'], subset['silhouette'], marker='o', label=f'min_samples={min_samples}')
plt.title('轮廓系数确定最优参数(越大越好)')
plt.xlabel('eps')
plt.ylabel('轮廓系数')
plt.legend()
plt.grid(True)
# CH 指数图
plt.subplot(2, 2, 2)
for min_samples in min_samples_range:
subset = results_df[results_df['min_samples'] == min_samples]
plt.plot(subset['eps'], subset['ch_score'], marker='o', label=f'min_samples={min_samples}')
plt.title('Calinski-Harabasz 指数确定最优参数(越大越好)')
plt.xlabel('eps')
plt.ylabel('CH 指数')
plt.legend()
plt.grid(True)
# DB 指数图
plt.subplot(2, 2, 3)
for min_samples in min_samples_range:
subset = results_df[results_df['min_samples'] == min_samples]
plt.plot(subset['eps'], subset['db_score'], marker='o', label=f'min_samples={min_samples}')
plt.title('Davies-Bouldin 指数确定最优参数(越小越好)')
plt.xlabel('eps')
plt.ylabel('DB 指数')
plt.legend()
plt.grid(True)
# 簇数量图
plt.subplot(2, 2, 4)
for min_samples in min_samples_range:
subset = results_df[results_df['min_samples'] == min_samples]
plt.plot(subset['eps'], subset['n_clusters'], marker='o', label=f'min_samples={min_samples}')
plt.title('簇数量变化')
plt.xlabel('eps')
plt.ylabel('簇数量')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()通过排除噪声,选出最佳EPS和min_samples
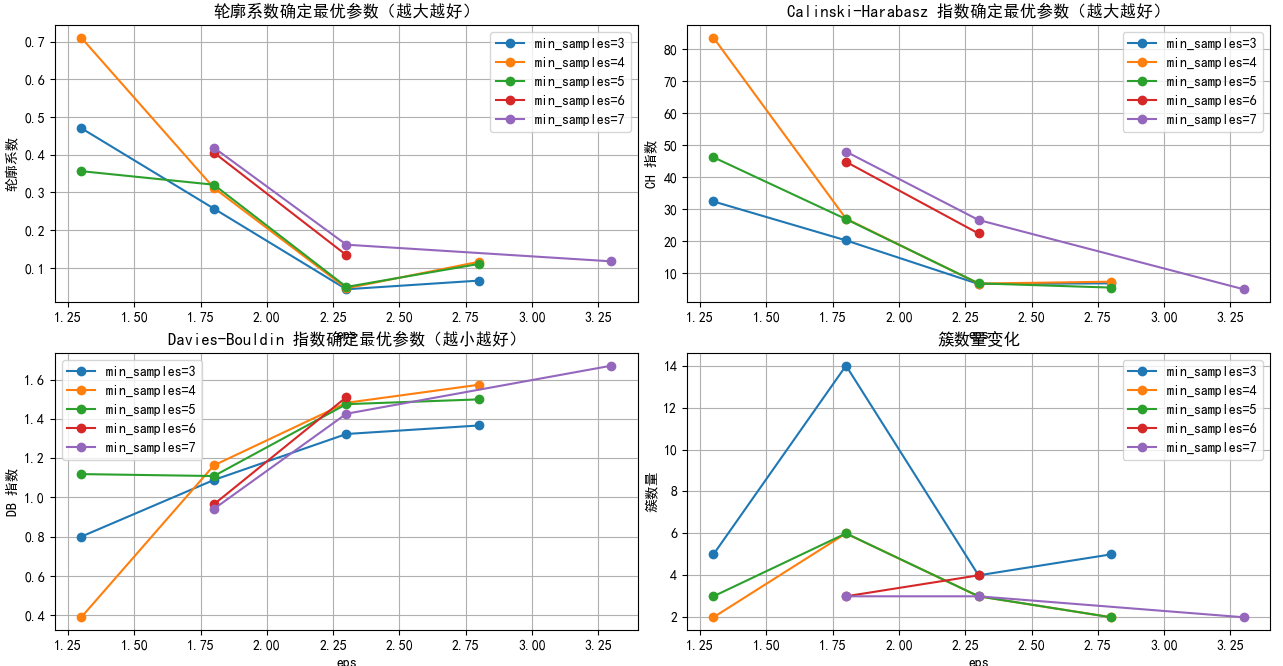
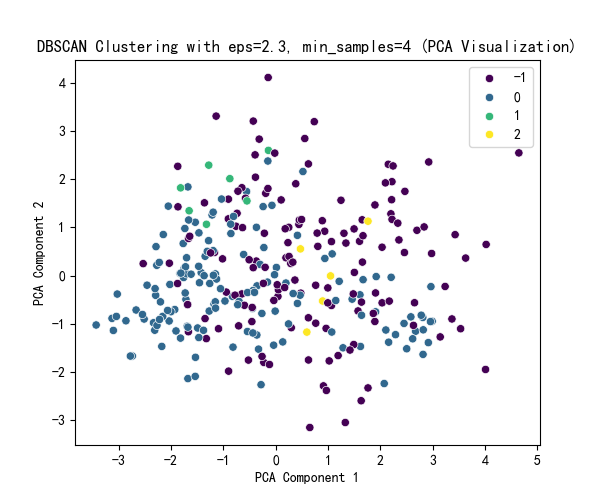
通过图片可以观察出eps最佳在2.25-2.50之间,min_samples最佳为4.
# 选择 eps 和 min_samples 值(根据图表选择最佳参数)
selected_eps = 2.3 # 根据图表调整
selected_min_samples = 4 # 根据图表调整
# 使用选择的参数进行 DBSCAN 聚类
dbscan = DBSCAN(eps=selected_eps, min_samples=selected_min_samples)
dbscan_labels = dbscan.fit_predict(x_scaled)
x['DBSCAN_Cluster'] = dbscan_labels
# 使用 PCA 降维到 2D 进行可视化
pca = PCA(n_components=2)
x_pca = pca.fit_transform(x_scaled)
# DBSCAN 聚类结果可视化
plt.figure(figsize=(6, 5))
sns.scatterplot(x=x_pca[:, 0], y=x_pca[:, 1], hue=dbscan_labels, palette='viridis')
plt.title(f'DBSCAN Clustering with eps={selected_eps}, min_samples={selected_min_samples} (PCA Visualization)')
plt.xlabel('PCA Component 1')
plt.ylabel('PCA Component 2')
plt.show()
# 打印 DBSCAN 聚类标签的分布
print(f"DBSCAN Cluster labels (eps={selected_eps}, min_samples={selected_min_samples}) added to X:")
print(x[['DBSCAN_Cluster']].value_counts())进行聚类
层次聚类
n_clusters_range = range(2, 11) # 测试簇数量从 2 到 10
silhouette_scores = []
ch_scores = []
db_scores = []
for n_clusters in n_clusters_range:
agglo = AgglomerativeClustering(n_clusters=n_clusters, linkage='ward') # 使用 Ward 准则合并簇
agglo_labels = agglo.fit_predict(x_scaled)
# 计算评估指标
silhouette = silhouette_score(x_scaled, agglo_labels)
ch = calinski_harabasz_score(x_scaled, agglo_labels)
db = davies_bouldin_score(x_scaled, agglo_labels)
silhouette_scores.append(silhouette)
ch_scores.append(ch)
db_scores.append(db)
print(f"n_clusters={n_clusters}, 轮廓系数: {silhouette:.3f}, CH 指数: {ch:.2f}, DB 指数: {db:.3f}")
# 绘制评估指标图
plt.figure(figsize=(15, 5))
# 轮廓系数图
plt.subplot(1, 3, 1)
plt.plot(n_clusters_range, silhouette_scores, marker='o')
plt.title('轮廓系数确定最优簇数(越大越好)')
plt.xlabel('簇数量 (n_clusters)')
plt.ylabel('轮廓系数')
plt.grid(True)
# CH 指数图
plt.subplot(1, 3, 2)
plt.plot(n_clusters_range, ch_scores, marker='o')
plt.title('Calinski-Harabasz 指数确定最优簇数(越大越好)')
plt.xlabel('簇数量 (n_clusters)')
plt.ylabel('CH 指数')
plt.grid(True)
# DB 指数图
plt.subplot(1, 3, 3)
plt.plot(n_clusters_range, db_scores, marker='o')
plt.title('Davies-Bouldin 指数确定最优簇数(越小越好)')
plt.xlabel('簇数量 (n_clusters)')
plt.ylabel('DB 指数')
plt.grid(True)
plt.tight_layout()
plt.show()
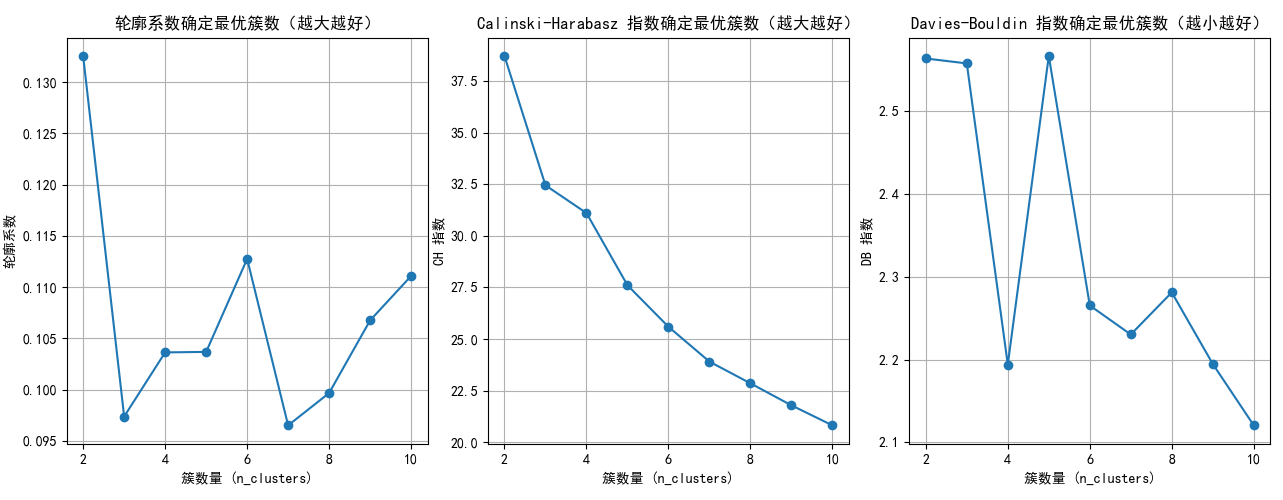
根据图片可以大致是判断出min_samples为2,4,10均可,我尝试了4进行聚类。
selected_n_clusters = 4 # 示例值,根据图表调整
# 使用选择的簇数进行 Agglomerative Clustering 聚类
agglo = AgglomerativeClustering(n_clusters=selected_n_clusters, linkage='ward')
agglo_labels = agglo.fit_predict(x_scaled)
x['Agglo_Cluster'] = agglo_labels
# 使用 PCA 降维到 2D 进行可视化
pca = PCA(n_components=2)
x_pca = pca.fit_transform(x_scaled)
# Agglomerative Clustering 聚类结果可视化
plt.figure(figsize=(6, 5))
sns.scatterplot(x=x_pca[:, 0], y=x_pca[:, 1], hue=agglo_labels, palette='viridis')
plt.title(f'Agglomerative Clustering with n_clusters={selected_n_clusters} (PCA Visualization)')
plt.xlabel('PCA Component 1')
plt.ylabel('PCA Component 2')
plt.show()
# 打印 Agglomerative Clustering 聚类标签的分布
print(f"Agglomerative Cluster labels (n_clusters={selected_n_clusters}) added to x:")
print(x[['Agglo_Cluster']].value_counts())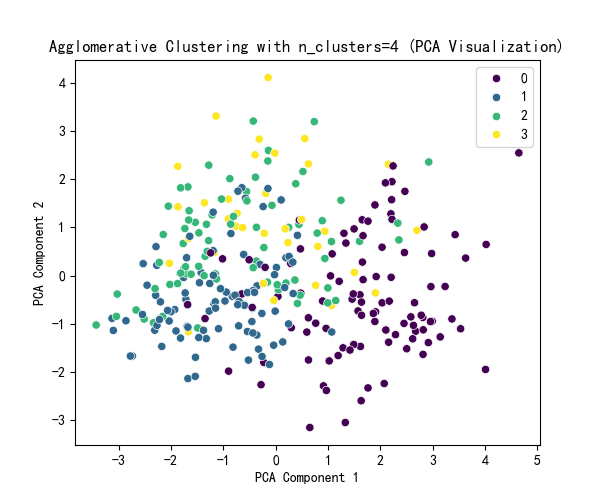
层次聚类的树状图可视化
from scipy.cluster import hierarchy
import matplotlib.pyplot as plt
# 假设 X_scaled 是标准化后的数据
# 计算层次聚类的链接矩阵
Z = hierarchy.linkage(X_scaled, method='ward') # 'ward' 是常用的合并准则
# 绘制树状图
plt.figure(figsize=(10, 6))
hierarchy.dendrogram(Z, truncate_mode='level', p=3) # p 控制显示的层次深度
# hierarchy.dendrogram(Z, truncate_mode='level') # 不用p这个参数,可以显示全部的深度
plt.title('Dendrogram for Agglomerative Clustering')
plt.xlabel('Cluster Size')
plt.ylabel('Distance')
plt.show()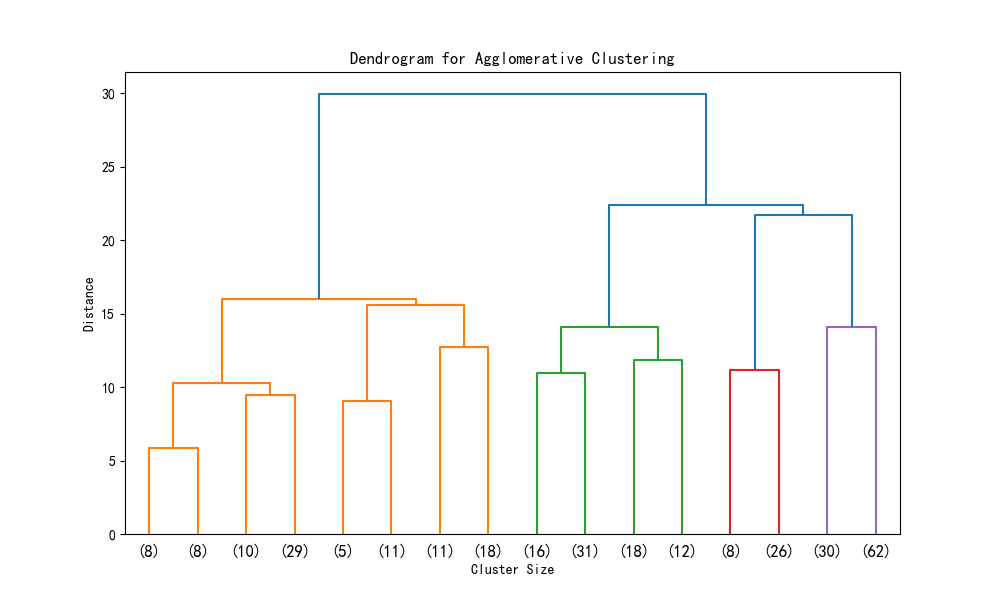





















 819
819

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








