剑指offer： 矩形覆盖

题目描述：我们可以用2*1的小矩形横着或者竖着去覆盖更大的矩形。请问用n个2*1的小矩形无重叠地覆盖一个2*n的大矩形，总共有多少种方法？

 

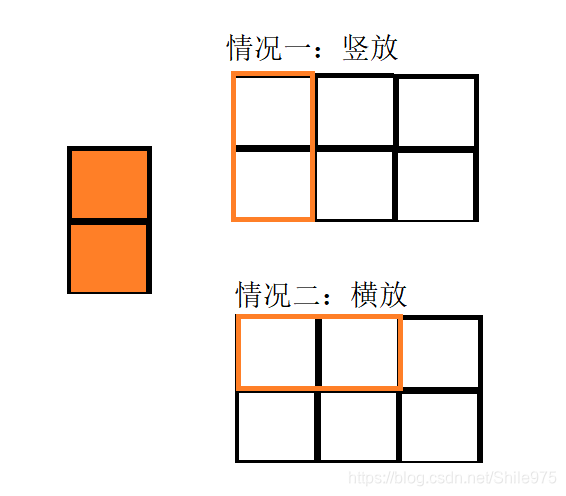
由图分析，其实也是一种分情况的情景：第一块是竖放还是横放，决定了下一步的放置方式。

使用递归方式解决。

class Solution {
public:
	int rectCover(int number) 
	{
		int count = 0;
		if (number == 0)
			return 0;
		if (number == 1)
			return 1;
		if (number == 2)
			return 2;
		else
			return rectCover(number - 1) + rectCover(number - 2);
	}
};