13_Pyton之递归函数

最新推荐文章于 2023-06-18 20:05:10 发布

原创最新推荐文章于 2023-06-18 20:05:10 发布 · 289 阅读

0 ·

CC 4.0 BY-SA版权

Python 专栏收录该内容

45 篇文章

订阅专栏

本文探讨了Python中的递归函数，包括如何利用递归计算阶乘、实现斐波那契数列以及解决经典的汉诺塔问题。通过这些实例，展示了递归在解决复杂问题时的强大能力。

一、递归函数
已知: 函数可以调用函数。结论: 一个函数在内部调用自己本身,这个函数就是递归函数。

(1)计算阶乘 factorial： n! = 1 * 2 * 3 * … * n

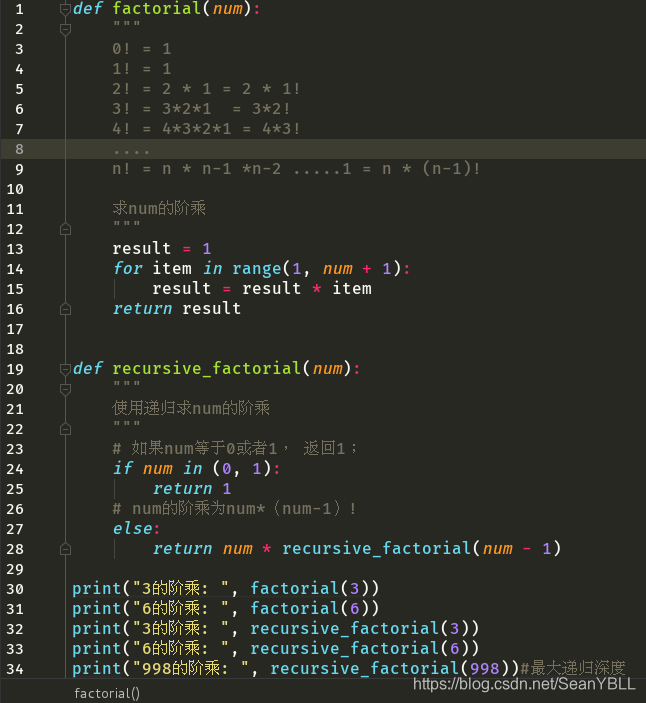
def factorial(num):
    """
    0! = 1
    1! = 1
    2! = 2 * 1 = 2 * 1!
    3! = 3*2*1  = 3*2!
    4! = 4*3*2*1 = 4*3!
    ....
    n! = n * n-1 *n-2 .....1 = n * (n-1)!

    求num的阶乘
    """
    result = 1
    for item in range(1, num + 1):
        result = result * item
    return result


def recursive_factorial(num):
    """
    使用递归求num的阶乘
    """
    # 如果num等于0或者1， 返回1；
    if num in (0, 1):
        return 1
    # num的阶乘为num*（num-1）!
    else:
        return num * recursive_factorial(num - 1)

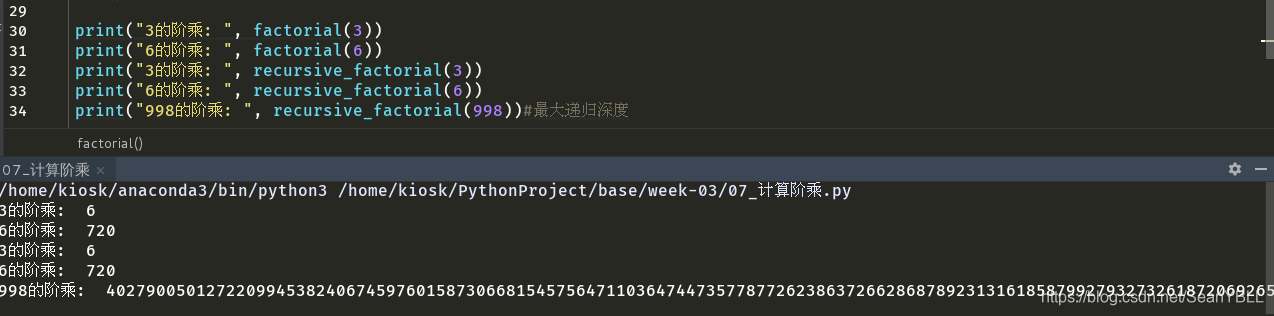
print("3的阶乘: ", factorial(3))
print("6的阶乘: ", factorial(6))
print("3的阶乘: ", recursive_factorial(3))
print("6的阶乘: ", recursive_factorial(6))
print("998的阶乘: ", recursive_factorial(998))  ##最大递归深度

在这里插入图片描述

(2)斐波那契数列（Fibonacci sequence）

"""
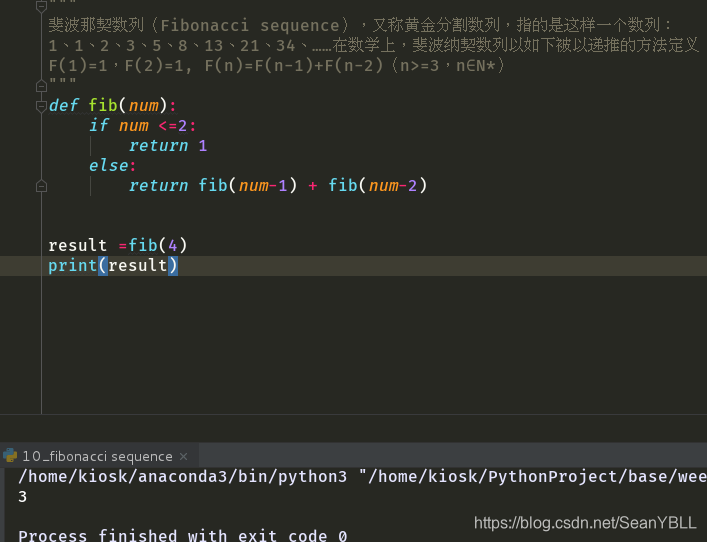
斐波那契数列（Fibonacci sequence），又称黄金分割数列，指的是这样一个数列：
1、1、2、3、5、8、13、21、34、……在数学上，斐波纳契数列以如下被以递推的方法定义：
F(1)=1，F(2)=1, F(n)=F(n-1)+F(n-2)（n>=3，n∈N*）
"""
def fib(num):
    if num <=2:
        return 1
    else:
        return fib(num-1) + fib(num-2)


result =fib(4)
print(result)

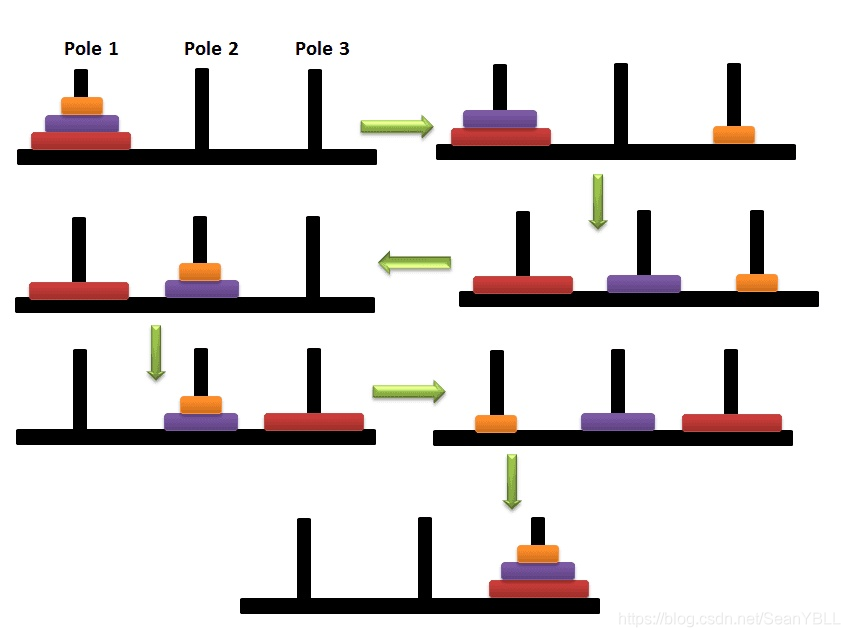
在这里插入图片描述

(3)汉诺塔问题
汉诺塔：汉诺塔（又称河内塔）问题是源于印度一个古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。
在这里插入图片描述

movecount = 0
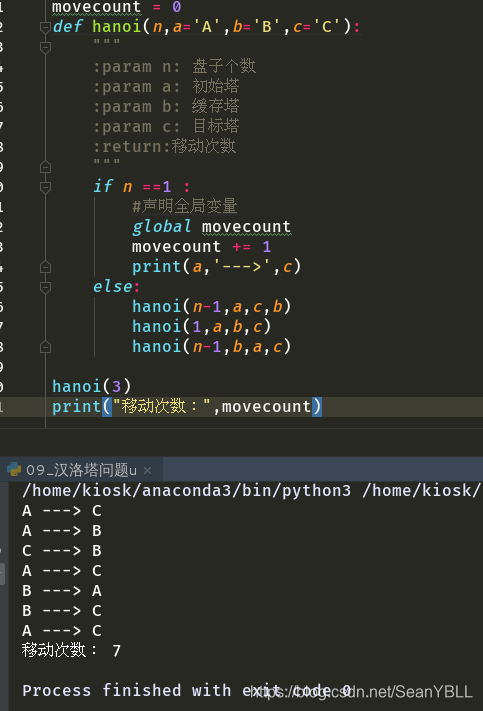
def hanoi(n,a='A',b='B',c='C'):
    """
    :param n: 盘子个数
    :param a: 初始塔
    :param b: 缓存塔
    :param c: 目标塔
    :return:移动次数
    """
    if n ==1 :
        #声明全局变量
        global movecount
        movecount += 1
        print(a,'--->',c)
    else:
        hanoi(n-1,a,c,b)
        hanoi(1,a,b,c)
        hanoi(n-1,b,a,c)

hanoi(3)
print("移动次数：",movecount)

在这里插入图片描述