A. 小红的图
题目描述
平面上有一个 2×2 的格子,小红初始在第 a 列,第 b 行,她想知道自己在格子的左上、左下、右上还是右下位置,请你帮帮她。输入描述:
第一行输入两个整数 a,b(1≦a,b≦2)。
输出描述:
对于小红在左上、左下、右上、右下,分别输出 LU、LD、RU、RD。
解题思路:注意是先输入的列再输入的行
import java.util.Scanner;
public class Main{
public static void main(String[] args){
Scanner sc = new Scanner(System.in);
int b = sc.nextInt();
int a = sc.nextInt();
if(a==1 && b==1){
System.out.println("LU");
}else if(a==1 && b==2){
System.out.println("RU");
}else if(a==2 && b==2){
System.out.println("RD");
}else{
System.out.println("LD");
}
}
}
B. 小红的菊花
题目描述
小红拿到了一个由 n 个点组成的菊花树,现在她想知道菊花的中心点(即与除自身外所有节点均相连的点)的编号,请你帮帮她。
【名词解释】
菊花:一种特殊的树,满足存在 u 使得所有除 u 外点均与 u 相连。
输入描述:
第一行输入一个整数 n(3≦n≦100)。
之后的 n−1 行,每行输入两个整数 ui,vi(1≦ui,vi≦n,ui≠vi),代表 ui,vi 之间有一条边。特殊的,保证所给出的图是一个菊花。
输出描述:
输出一个整数,代表中心点的编号。
解题思路:统计度数为n-1的点,用deg数组进行统计各个点的度数
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int[] deg = new int[n + 1];
for (int i = 0; i < n - 1; i++) {
int u = sc.nextInt();
int v = sc.nextInt();
deg[u]++;
deg[v]++;
}
sc.close();
for (int i = 1; i <= n; i++) {
if (deg[i] == n - 1) {
System.out.println(i);
}
}
}
}
C. 小红的好矩形
题目描述
在平面直角坐标系中,小红定义一个矩形是好矩形,当且仅当其所有边均平行于坐标轴,且面积为 2。
现在小红要选出四个横坐标在 [0,n]内,纵坐标在 [0,m] 内的整点,使得这四个点能组成一个矩形,且矩形是好矩形。
小红想知道有多少种选法,请你帮帮她。输入描述:
第一行输入两个整数 n,m(1≦n,m≦2×10^5)
输出描述:
输出一个整数,代表合法的方案数。
解题思路:
面积是2,因此只有1 * 2 或者 2 * 1两种情况
第一种情况的话,
[0, n] 选 长度 为1 的段,有n中选法
[0, m] 选长度为2的段,有m-1中选法
第二种情况则相反
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt(), m = sc.nextInt();
int x0 = Math.max(0,m-1),y = n;
int x1 = Math.max(0,n-1),y1 = m;
long ans = 1L * x0 * y + 1L * x1 * y1;
System.out.println(ans);
}
}
D. 小红嫁接
题目描述
小芳有一颗 n 个节点的树,但小红更喜欢链。为了把这棵树变成链,小红可以进行如下操作:
∙选择任意一条边,其连接两个点 u,v。现在将这条边断开,之后在点 u 所在连通块中任选一个节点,向点 v 连边。
小红想知道,要把这棵树变成链最少需要几次操作?
输入描述:
第一行输入一个整数 n(1≦n≦2×10^5)。
之后的 n−1 行,每行输入两个整数 ui,vi(1≦ui,vi≦n),代表有一条边连接 ui,vi。输出描述:
输出一个整数,代表小红所需的最少次数。
示例1输入
5
1 2
1 3
1 4
4 5
输出
1
解题思路:
统计每个点的度数,对于一条链来说,两端节点的度数都为1,中间各个部分的节点都为2
操作一次的话,就是将多余节点连接到树的叶子节点上【度数为1的节点】,因此总操作次数就是 每个节点所连接的多余度节点的和【Math.max(0, deg[i] -2 )】
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int[] deg = new int[n + 1];
for (int i = 0; i < n - 1; i++) {
int u = sc.nextInt();
int v = sc.nextInt();
deg[u]++;
deg[v]++;
}
sc.close();
long ans = 0L;
for (int i = 1; i <= n; i++) {
if (deg[i] > 2) ans += (deg[i] - 2);
}
System.out.println(ans);
}
}
E. 小红玩马
题目描述
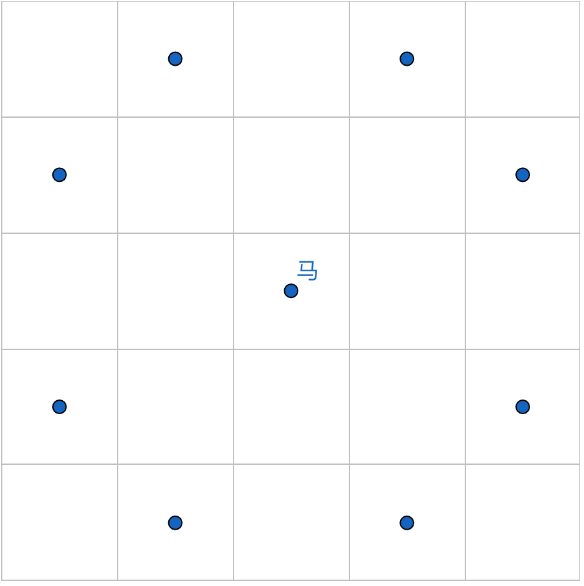
小红在一个 n×m 的棋盘中玩国际象棋。一开始,在 (x1,y1) 位置有一个马,小红想要使用恰好 k 步将其移动到 (x2,y2),请你帮小红找到一个可能的移动路径。(k 步之后马的位置在(x2,y2)即可。)
马能走到的位置如下图所示:
输入描述:
第一行输入三个整数 n,m,k(1≦n,m≦1000,1≦k≦2×10^5)第二行输入四个整数 x1,y1,x2,y2(1≦x1,x2≦n,1≦y1,y2≦m)。
输出描述:
如果不存在合法的方案,请输出 No;否则输出 Yes,并在之后的 k 行内,每行输出两个整数 xi,yi,代表第 i 步走到了 (xi,yi)。
如果存在多个解决方案,您可以输出任意一个,系统会自动判定是否正确。注意,自测运行功能可能因此返回错误结果,请自行检查答案正确性。
示例1输入
3 3 3
1 1 1 2
输出
Yes
2 3
3 1
1 2
解题思路:
1. 步数必须满足k,提前到达后,也需要通过来回往返来消耗多余偶数步数
import java.util.*;
public class Main {
private static final int[] DX = {1,1,2,2,-1,-1,-2,-2};
private static final int[] DY = {2,-2,1,-1,2,-2,1,-1};
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int m = sc.nextInt();
int k = sc.nextInt();
int x1 = sc.nextInt() - 1;
int y1 = sc.nextInt() - 1;
int x2 = sc.nextInt() - 1;
int y2 = sc.nextInt() - 1;
sc.close();
int N = n * m;
int s = x1 * m + y1;
int t = x2 * m + y2;
int[] dist = new int[N];
Arrays.fill(dist, -1);
int[] pre = new int[N];
Arrays.fill(pre, -1);
int[] q = new int[N];
int head = 0, tail = 0;
q[tail++] = s;
dist[s] = 0;
boolean flag = false;
while (head < tail) {
int u = q[head++];
if (u == t) { flag = true; break; }
int ux = u / m, uy = u % m;
for (int d = 0; d < 8; d++) {
int vx = ux + DX[d], vy = uy + DY[d];
if (vx < 0 || vx >= n || vy < 0 || vy >= m) continue;
int v = vx * m + vy;
if (dist[v] == -1) {
dist[v] = dist[u] + 1;
pre[v] = u;
q[tail++] = v;
}
}
}
if (dist[t] == -1 || dist[t] > k || ((k - dist[t]) & 1) == 1) {
System.out.println("No");
return;
}
ArrayList<Integer> path = new ArrayList<>();
int cur = t;
while (cur != -1) {
path.add(cur);
cur = pre[cur];
}
Collections.reverse(path);
int insertIdx = -1;
for (int i = 0; i < path.size(); i++) {
int id = path.get(i);
int x = id / m, y = id % m;
boolean hasNeigh = false;
for (int d = 0; d < 8; d++) {
int nx = x + DX[d], ny = y + DY[d];
if (nx >= 0 && nx < n && ny >= 0 && ny < m) {
hasNeigh = true; break;
}
}
if (hasNeigh) { insertIdx = i; break; }
}
if (insertIdx == -1) {
if (k == 0 && dist[t] == 0) {
System.out.println("Yes");
return;
} else {
System.out.println("No");
return;
}
}
int extraPairs = (k - dist[t]) / 2;
ArrayList<int[]> moves = new ArrayList<>(k);
int pathLen = path.size();
int position = path.get(0);
for (int idx = 0; idx < pathLen; idx++) {
if (idx == insertIdx && extraPairs > 0) {
int x = position / m, y = position % m;
int neigh = -1;
for (int d = 0; d < 8; d++) {
int nx = x + DX[d], ny = y + DY[d];
if (nx >= 0 && nx < n && ny >= 0 && ny < m) {
neigh = nx * m + ny;
break;
}
}
for (int tpair = 0; tpair < extraPairs; tpair++) {
moves.add(new int[]{neigh / m + 1, neigh % m + 1});
moves.add(new int[]{position / m + 1, position % m + 1});
}
}
if (idx + 1 < pathLen) {
int next = path.get(idx + 1);
moves.add(new int[]{next / m + 1, next % m + 1});
position = next;
}
}
if (moves.size() != k) {
System.out.println("No");
return;
}
StringBuilder sb = new StringBuilder();
sb.append("Yes\n");
for (int[] p : moves) {
sb.append(p[0]).append(' ').append(p[1]).append('\n');
}
System.out.print(sb.toString());
}
}
F. 小红的⑨
题目描述
小红定义树上两个点的距离为这两点之间简单路径经过的边数。
小红拿到了一棵有 n 个节点的树,现在她想知道对于这棵树的每个节点,距离恰好为 9 的节点有多少个,请你帮帮她。输入描述:
第一行输入一个整数 n(1≦n≦2×10^5)之后的 n−1 行,每行输入两个整数 u,v(1≦u,v≦n),代表点 u,v 之间有一条边。
输出描述:
输出 n 个整数,依次代表对于 1 到 n 号点,距离为 9 的节点有多少个。
示例1输入
10
1 2
2 3
3 4
4 5
5 6
6 7
7 8
8 9
9 10
输出
1 0 0 0 0 0 0 0 0 1
import java.util.*;
public class Main {
private static final int K = 9;
public static void main(String[] args) throws Exception {
Scanner fs = new Scanner(System.in);
int n = fs.nextInt();
ArrayList<Integer>[] g = new ArrayList[n + 1];
for (int i = 1; i <= n; i++) g[i] = new ArrayList<>();
for (int i = 0; i < n - 1; i++) {
int u = fs.nextInt();
int v = fs.nextInt();
g[u].add(v);
g[v].add(u);
}
int[][] down = new int[n + 1][K + 1];
int[][] up = new int[n + 1][K + 1];
int[] parent = new int[n + 1];
Arrays.fill(parent, 0);
ArrayList<Integer> order = new ArrayList<>(n);
ArrayDeque<Integer> stack = new ArrayDeque<>();
stack.push(1);
parent[1] = 0;
while (!stack.isEmpty()) {
int u = stack.pop();
order.add(u);
for (int v : g[u]) {
if (v == parent[u]) continue;
parent[v] = u;
stack.push(v);
}
}
for (int idx = order.size() - 1; idx >= 0; --idx) {
int u = order.get(idx);
Arrays.fill(down[u], 0);
down[u][0] = 1;
for (int v : g[u]) {
if (v == parent[u]) continue;
for (int d = 1; d <= K; ++d) {
down[u][d] += down[v][d - 1];
}
}
}
long[] ans = new long[n + 1];
for (int u : order) {
int[] all = new int[K + 1];
for (int d = 0; d <= K; d++) {
all[d] = down[u][d] + up[u][d];
}
ans[u] = all[K];
for (int v : g[u]) {
if (v == parent[u]) continue;
Arrays.fill(up[v], 0);
if (K >= 1) up[v][1] = 1;
for (int d = 2; d <= K; d++) {
int val = all[d - 1] - down[v][d - 2];
up[v][d] = val;
}
}
}
StringBuilder sb = new StringBuilder();
for (int i = 1; i <= n; i++) {
sb.append(ans[i]);
if (i < n) sb.append(' ');
}
sb.append('\n');
System.out.print(sb.toString());
}
}
感谢大家的点赞和关注,你们的支持是我创作的动力!






















 979
979










