贪心算法知识整理

---

一、贪心算法的概念

       贪心算法是一种对某些求最优解问题的更简单、更迅速的设计技术。贪心算法的特点是一步一步地进行，常以当前情况为基础根据某个优化测度作最优选择，而不考虑各种可能的整体情况，省去了为找最优解要穷尽所有可能而必须耗费的大量时间。贪心算法采用自顶向下，以迭代的方法做出相继的贪心选择，每做一次贪心选择，就将所求问题简化为一个规模更小的子问题，通过每一步贪心选择，可得到问题的一个最优解。虽然每一步上都要保证能获得局部最优解，但由此产生的全局解有时不一定是最优的，所以贪心算法不要回溯。

---

二、贪心算法的基本要素

1、贪心选择性质

       一个问题的整体最优解可通过一系列局部的最优解的选择达到，并且每次的选择可以依赖以前作出的选择，但不依赖于后面要作出的选择。这就是贪心选择性质。对于一个具体问题，要确定它是否具有贪心选择性质，必须证明每一步所作的贪心选择最终导致问题的整体最优解  。

2、最优子结构性质

        当一个问题的最优解包含其子问题的最优解时，称此问题具有最优子结构性质。问题的最优子结构性质是该问题可用贪心法求解的关键所在。在实际应用中，至于什么问题具有什么样的贪心选择性质是不确定的，需要具体问题具体分析 。

---

三、贪心算法的步骤

贪心算法一般按如下步骤进行：

①建立数学模型来描述问题 。

②把求解的问题分成若干个子问题 。

③对每个子问题求解，得到子问题的局部最优解。

④把子问题的解局部最优解合成原来解问题的一个解 。

---

四、贪心算法的证明

1.证明具有最优结构性质。

2.证明满足贪心选择性质。

---

五、例子

问题描述：
         哈夫曼编码是广泛地用于数据文件压缩的十分有效的编码方法。其压缩率通常在20%～90%之间。哈夫曼编码算法用字符在文件中出现的频率表来建立一个用0，1串表示各字符的最优表示方式。一个包含100,000个字符的文件，各字符出现频率不同，如下表所示：

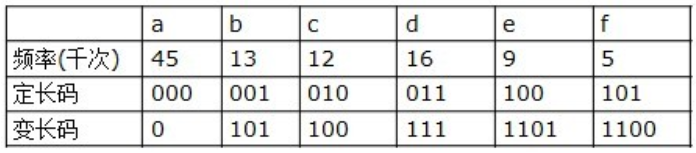
        有多种方式表示文件中的信息，若用0,1码表示字符的方法，即每个字符用唯一的一个0,1串表示。若采用定长编码表示，则需要3位表示一个字符，整个文件编码需要300,000位；若采用变长编码表示，给频率高的字符较短的编码；频率低的字符较长的编码，达到整体编码减少的目的，则整个文件编码需要（45×1+13×3+12×3+16×3+9×4+5×4）×1000=224,000位，由此可见，变长码比定长码方案好，总码长减小约25%。

输入格式:
输入数据的第一行有1个正整数n，表示有n个需要编码的字符。接下来的n行中，每行有一个字符和一个整数，表示要编码的字符和此字符在文本中出现的频率。

输出格式：
输出每个字符的边长Huffman编码。

输入样例：

6
45
13
12
16
9
5

输出样例：

a:0
b:101
c:100
d:111
e:1101
f:1100

 分析：

       选择使用优先队列对存储结构进行优化，取出队列中最小的两个节点构成一棵再放回队列，直至最终构建成一棵树，最终遍历每个叶子节点，取叶子同时从叶子节点向跟节点遍历，在跟左为0，跟右为1。

#include<iostream>
#include <queue>
using namespace std;

struct point{
	char value;
	int weight;
	struct point* par;
	struct point* left;
	struct point* right;
};

struct cmp{
	bool operator()(point* a, point* b){
		return a->weight>b->weight;
	}
};

int main(){
	int n,*x;
	cin>>n;
	vector <point*> p(n); 
	priority_queue<point*, vector<point*>, cmp> myque;
	for(int i=0;i<n;i++){
		p[i]=new point;
		cin>>p[i]->weight;
		p[i]->value='a'+i;
		p[i]->par=p[i]->left=p[i]->right=NULL;
		myque.push(p[i]);
	}
	point *t1;
	for(t1=myque.top(),myque.pop();!myque.empty();t1=myque.top(),myque.pop()){
		point *t2, *t3;
		t2=myque.top();
		myque.pop();
		t3=new point;
		t3->left=t1;
		t3->right=t2;
		t3->par=NULL;
		t3->value='0';
		t3->weight=t1->weight+t2->weight;
		t1->par=t3;
		t2->par=t3;
		myque.push(t3);
	}
	point* result =t1;
	for(int i=0;i<n;i++){
		string str="";
		point *tp, *t;
		tp=p[i];
		if(tp->par==NULL)
			str="0";
		while(tp->par!=NULL){
			t=tp->par;
			if(t->left==tp)
				str="0"+str;
			else
				str="1"+str;
			tp=tp->par;
		}
		cout<<p[i]->value<<":"+str<<endl;
	}
	return 0;
}