目录
二叉搜索树

二叉搜索树主要是例如一个小树有两个节点,左子树小,右子树大。
二叉搜索树用于去重(插入如果存有值就不插入),查找,排序。
二叉搜索树查找一个整形数字,最好是高度次,比如查找10万的数字只需要查找20次,因为2^20次是10万,查找1亿的数字,只需要查找30次,最差是O(N),这倒不如用顺序表,因为如果查找前插入的数字是有序的,会导致一边全是存的值,成一个"单叉数"了。
//以下代码是二叉搜索树的框架,由于比较简单,所以就不一一赘述了。
//主要就是理解左边插入比节点的大的值,右边插入比节点小的值,最后整体上看的出左边值都比较小,右边值都比较大。
//从Insert来说开始写代码是比较容易的,Find也差不多,Erase需要深刻理解,因为Erase要考虑
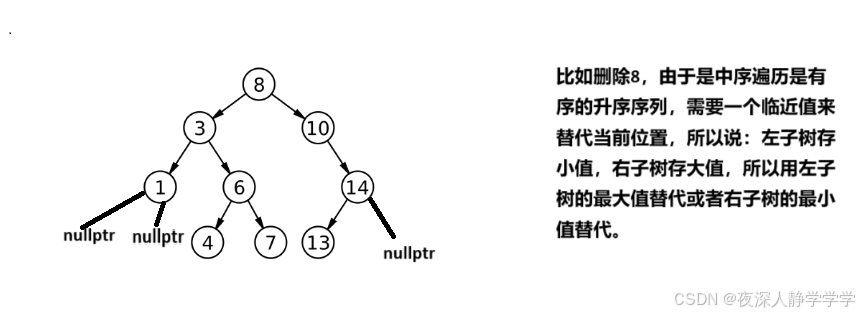
三种情况拿上面的二叉搜索树为例,删除1没有子节点,要delete 1的节点,并且要将父节点的左子树更新成nullptr;删除14有一个子节点,并且要将父节点的右子树改为14的左节点,综上1和2种情况可以归为一类,即有一个和没有子节点的节点删除之前,要将父节点的当前节点的一边指向当前节点的存在子节点的一边,具体情况根据代码来帮助理解,见Erase成员函数。
综上,第二种情况就是有两个节点的
二叉搜索树代码:
#pragma once
#include <iostream>
using namespace std;
template<class K>//单参数模版
struct BSTNode//二叉搜索树的节点
{
BSTNode(const K& key)//初始化列表
:_key(key),
_left(nullptr),
_right(nullptr)
{}
K _key;//节点的值
BSTNode* _left;//左节点
BSTNode* _right;//右节点
};
template<class K>
class BSTree//二叉搜索树
{
typedef BSTNode<K> Node;
public:
bool Insert(const K& key)//插入
{
if (_root == nullptr)
{
_root = new Node(key);
return true;
}
else
{
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else
{
return false;
}
}
cur = new Node(key);
if (parent->_key > key)
{
parent->_left = cur;
}
else
{
parent->_right = cur;
}
return true;
}
}
bool Find(const K& key)//查找
{
Node* cur = _root;
while (cur)
{
if (cur->_key > key)
{
cur = cur->_left;
}
else if (cur->_key < key)
{
cur = cur->_right;
}
else
{
return true;
}
}
return false;
}
bool Erase(const K& key)//删除
{
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else
{
//0个孩子和1个孩子的情况//归并为一类
if (cur->_left == nullptr)
{
if (parent == nullptr)//~!!!!重要
{
_root = cur->_right;
}//~!!!!
else
{
if (parent->_left == cur)
{
parent->_left = cur->_right;
}
else
{
parent->_right = cur->_right;
}
}
delete cur;
return true;
}
else if (cur->_right == nullptr)
{
if (parent == nullptr)
{
_root = cur->_left;
}
else
{
if (parent->_left == cur)
{
parent->_left = cur->_left;
}
else
{
parent->_right = cur->_left;
}
}
delete cur;
return true;
}
else
{
//2个孩子的情况
//找右子树的最小值或者左子树的最大值
Node* RightMinP = cur;
Node* RightMin = cur->_right;
while (RightMin->_left)
{
RightMinP = RightMin;
RightMin = RightMin->_left;
}
cur->_key = RightMin->_key;
if (RightMinP->_left == RightMin)
{
RightMinP->_left = RightMin->_right;
}
else
{
RightMinP->_right = RightMin->_right;
}
delete RightMin;
return true;
}
}
}
return false;
}
//中序遍历函数
void InOrder()
{
_InOrder(_root);
cout << endl;
}
void _InOrder(Node* root)
{
if (root == nullptr)
{
return;
}
_InOrder(root->_left);
cout << root->_key << " ";
_InOrder(root->_right);
}
private:
Node* _root = nullptr;//给缺省值
};key和key/value
key就是查找这个key值,key/value就是通过key查找value,将key和value联系起来。
key就是上面代码的表示的搜索二叉树,
key/value就是在key的基础上添加一个变量给节点,需要修改的就是初始化列表的参数,形参,find需要返回节点,
insert需要传key,value,以及BSTNode类和BSTree类中修改typedef模板参数等。
修改代码如下,
#pragma once
#include <iostream>
using namespace std;
template<class K,class V>//修改
struct BSTNode
{
BSTNode(const K& key,const V& value)//修改
:_key(key),
_value(value),//修改
_left(nullptr),
_right(nullptr)
{}
K _key;
V _value;//修改
BSTNode* _left;
BSTNode* _right;
};
template<class K,class V>//修改
class BSTree
{
typedef BSTNode<K,V> Node;//修改
public:
bool Insert(const K& key,const V& value)//修改
{
if (_root == nullptr)
{
_root = new Node(key,value);//修改
return true;
}
else
{
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else
{
return false;
}
}
cur = new Node(key,value);//修改
if (parent->_key > key)
{
parent->_left = cur;
}
else
{
parent->_right = cur;
}
return true;
}
}
Node* Find(const K& key)//修改返回值
{
Node* cur = _root;
while (cur)
{
if (cur->_key > key)
{
cur = cur->_left;
}
else if (cur->_key < key)
{
cur = cur->_right;
}
else
{
return cur;//修改
}
}
return nullptr;//修改
}
bool Erase(const K& key)
{
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else
{
//0个孩子和1个孩子的情况//归并为一类
if (cur->_left == nullptr)
{
if (parent == nullptr)//~!!!!重要
{
_root = cur->_right;
}//~!!!!
else
{
if (parent->_left == cur)
{
parent->_left = cur->_right;
}
else
{
parent->_right = cur->_right;
}
}
delete cur;
return true;
}
else if (cur->_right == nullptr)
{
if (parent == nullptr)
{
_root = cur->_left;
}
else
{
if (parent->_left == cur)
{
parent->_left = cur->_left;
}
else
{
parent->_right = cur->_left;
}
}
delete cur;
return true;
}
else
{
//2个孩子的情况
//找右子树的最小值或者左子树的最大值
Node* RightMinP = cur;
Node* RightMin = cur->_right;
while (RightMin->_left)
{
RightMinP = RightMin;
RightMin = RightMin->_left;
}
cur->_key = RightMin->_key;
if (RightMinP->_left == RightMin)
{
RightMinP->_left = RightMin->_right;
}
else
{
RightMinP->_right = RightMin->_right;
}
delete RightMin;
return true;
}
}
}
return false;
}
//中序遍历函数
void InOrder()
{
_InOrder(_root);
cout << endl;
}
void _InOrder(Node* root)
{
if (root == nullptr)
{
return;
}
_InOrder(root->_left);
cout << root->_key << "," << root->_value << " ";//修改
_InOrder(root->_right);
}
private:
Node* _root = nullptr;//给缺省值
};案例:
数据结构key类型用于比如门禁,通过人脸识别。
key/value用于比如查字典、统计key出现多少次等。
例如以下案例查字典、查水果出现多少次。
案例1:
#include <string>
int main()
{
//字典查单词
BSTree<string,string> t;
t.Insert("苹果","apple");
t.Insert("香蕉","banana");
t.Insert("梨","pear");
t.Insert("西瓜","watermelon");
//查找功能
string word;
while (cin >> word)
{
auto node = t.Find(word);//查找单词
if (node)
{
cout << "->" << node->_value << endl;//翻译成中文
}
else
{
cout << "没找到请从新输入" << ":" << endl;
}
}
return 0;
}案例2:
int main()
{
string arr[] = { "苹果", "西瓜", "苹果", "西瓜", "苹果", "苹果", "西瓜", "苹果", "香蕉", "苹果", "香蕉" };
BSTree<string,int> t;
for (const auto& str : arr)
{
//先查找水果在不在搜索树中
//1、不在,说明水果第一次出现,则插入<水果,1>
//2、在,则查找到的节点中水果对应的次数++
//BSTNode<string,int>* ret = t.Find(str)
auto ret = t.Find(str);
if (ret)
ret->_value++;
else
t.Insert(str, 1);
}
t.InOrder();//中序遍历查看
return 0;
}
第二个如何终止程序呢?
第一种方法:ctrl+c这种比较暴力,叫杀进程。
第二种方法:ctrl+z+回车键这种比较推荐。
小总结:
综上,由于二叉搜索树的局限性,当然实际上是用不到二叉搜索树的,因为效率低,所以就引入了“平衡”二叉搜索树。
C++不用造轮子,set就是key,map就是key,value。
set容器,底层其实是红黑树。
#incldue <set>

这里的T其实是key,第二个参数是仿函数,但是我们的里面有大于小于的情况,这里是less小于的比较器,那如果是比较大于的逻辑呢,其实就是换一下参数就好了。
if(cur->key <key)
if(key < cur->key)
当然实际上是例如Cmp()这样子的,上面只做参考。
#include <set>
int main()
{
set<int> s;
s.insert(7);
s.insert(8);
s.insert(1);
s.insert(2);
s.insert(5);
s.insert(0);
set<int>::iterator it = s.begin();
while (it != s.end())
{
cout << *it << " ";
it++;
}
cout << endl;
return 0;
}
#include <set>
int main()
{
set<int> s;
s.insert(7);
s.insert(8);
s.insert(1);
s.insert(2);
s.insert(5);
s.insert(0);
//set<int>::iterator it = s.begin();
auto it = s.begin();
while (it != s.end())
{
cout << *it << " ";
it++;
}
cout << endl;
for (auto& e : s)
{
cout << e << " ";
}
cout << endl;
return 0;
}

因为二叉搜索树可以去重,所以不会插入重复值。
构造函数
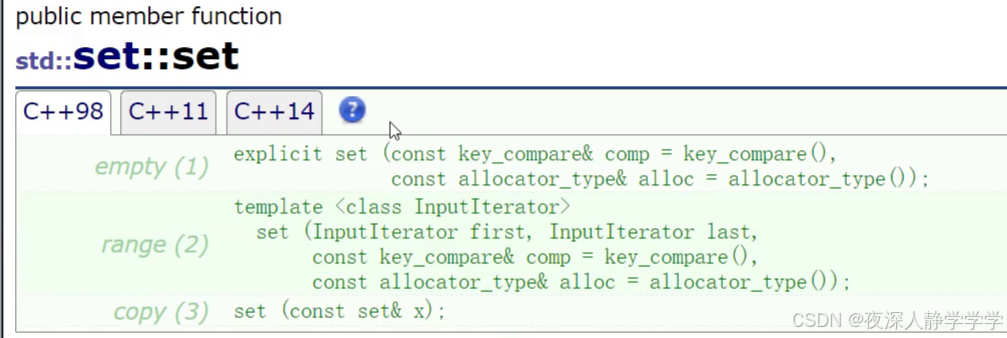
包括默认构造,拷贝构造,迭代器区间构造。
在看拷贝构造前先看一下析构函数如下:
//析构函数
~BSTree()
{
Destroy(_root);//套一层用递归遍历
_root = nullptr;
}
void Destroy(Node* root)//后续遍历,因为要删除子节点才能删除父节点。
{
if (root == nullptr)
return;
Destroy(root->_left);
Destroy(root->_right);
delete root;
}//代码测试
int main()
{
keyValue::BSTree<int,int> a;
a.Insert(1, 1);
keyValue::BSTree<int,int> b(a);//默认生成的浅拷贝
return 0;
}
析构报错。
所以,拷贝构造需要深拷贝,值拷贝,先父后子递归遍历,拷贝构造需要new node(key,value)。
//默认构造
BSTree() = default;
//拷贝构造
BSTree(const BSTree<T,V>& t)
{
_root = Copy(t._root);
}
//套一层方便递归实现。这里是后续遍历,因为需要先删除子节点后删除父节点。
Node* Copy(Node* root)
{
if (root == nullptr)
return nullptr;
Node* newRoot = new Node(root->_key, root->_value);
newRoot->_left = Copy(root->_left);
newRoot->_right = Copy(root->_right);
return newRoot;
}

set容器全展示图:
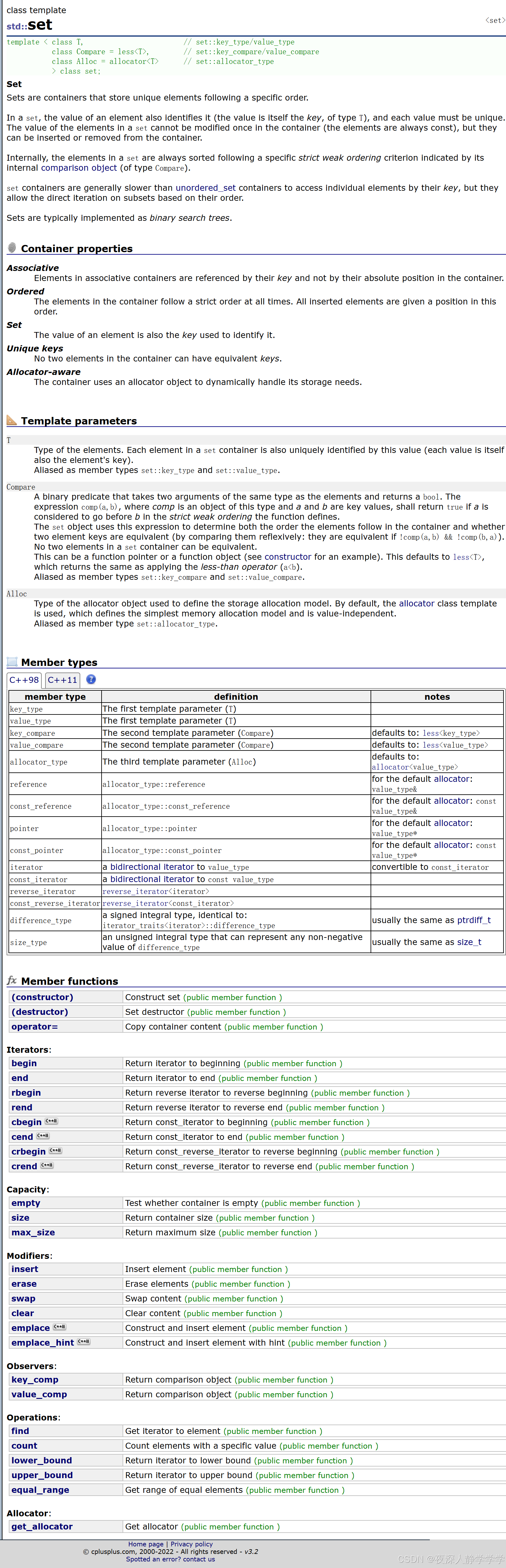
解释:
其他的成员函数其实之前都学过,大差不差。
迭代器的反向迭代器、swap就是交换一下root根节点的指针。

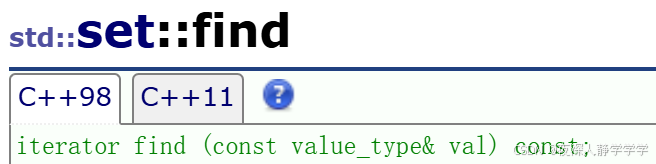
传迭代器erase
需要注意的是find如果找不到则返回end()位置的迭代器,如果将find和erase结合使用,如erase(s.find(1)),s表示set类的对象,如果1不在s中,返回end(),erase会报错,当然如果让其不报错,可以加上if。。else。。语句,提前判断如果迭代器为end(),则跳出判断语句,不进行erase。
传值erase
可以看到返回类型如下解释,表示返回删除成功的个数,可以通过if..else语句判断如果返回值为0则表示没有这个值,否则删除成功。

具体参考set参考
如果用算法库里的find和set的find有什么区别?

当然有区别了,库的是兼容所有的容器,时间复杂度为O(N),是暴力查找,set的find则是O(logN)
其次还有什么区别呢?
find返回值是迭代器,如果说需要判断某个值在不在还需要写一些代码,不如用count
s.count(x),x表示key,if...else判断,如果返回值为0则不在,不为0则在。


具体情况还用于multiset,multiset其实就是set的另一种,表示允许建值冗余,即可以加重复值。
lower_bound和upper_bound
共同使用,是帮助我们找一块区间进行处理,处理比如删除erase。
直接看代码,代码有详细解释。
// set::lower_bound/upper_bound
#include <iostream>
#include <set>
int main ()
{
std::set<int> myset;
std::set<int>::iterator itlow,itup;
for (int i=1; i<10; i++) myset.insert(i*10); // 10 20 30 40 50 60 70 80 90
itlow=myset.lower_bound (30); // 获取>=30
itup=myset.upper_bound (60); // 获取>60
//erase[30,60],为什么不是删除70呢?因为迭代器区间第二个参数必须是开区间,即erase[30,70)。
myset.erase(itlow,itup); // 10 20 70 80 90
std::cout << "myset contains:";
for (std::set<int>::iterator it=myset.begin(); it!=myset.end(); ++it)
std::cout << ' ' << *it;
std::cout << '\n';
return 0;
}了解一下,用的时候查一下文档就行了,set::lower_bound参考
equal_range找出相等的区间,multiset有用,这里用处不大。
multiset:允许建值冗余

但是如果插入重复的值,如何插入呢,由于跟set是有区别的。
如果相等怎么插入?
>=,插入到右边,如图:
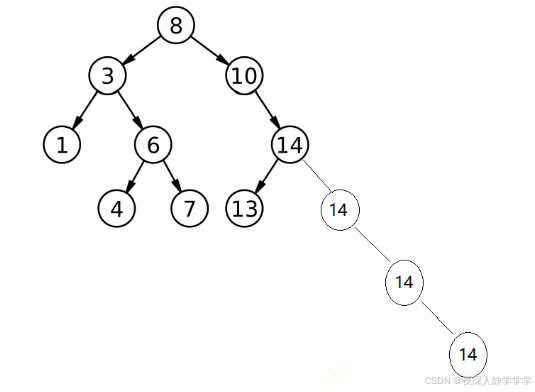
当然最后就算是插入到右边,也可能会旋转,插入到左边也可能会旋转。
所以在左边,右边重要吗?不重要,因为有可能插入到左边,也可能插入到右边。
当然multiset的接口不需要刻意学,因为基本上跟set一样,那么如果find查找一个值呢,返回的是第几个呢?
区别:
1,find查找x时,多个x在树种,返回中序第一个x。
2,允许相等的值插入。
这样规定,是有一定优势的。
如果说把所有的x都找出来,你怎么找?
看如下代码:


规定返回中序的第一个,这样是更有意义的。
当然multiset的count也是很有用的,用count来快速的统计一个值出现的次数。
那么如果用erase来删除指定的值呐?
当然,结果是删除所有出现这个值的位置。

所以,可以使用find来删除例如5第一次出现的位置。
当然也要考虑迭代器失效的问题,因为erase第一个5后,5的空间被释放,所以我们需要一个迭代器来存储返回值,即下一个值的位置的迭代器。
equle_range
表示找某个值相等的区间,比如传个9,会找到是9的区间{9,9,9,9};






















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








