图形学--Transformation

为什么突然写图形学的东西了呢，当然是学校要上这门课（摊 

2D Transformation

scale 缩放

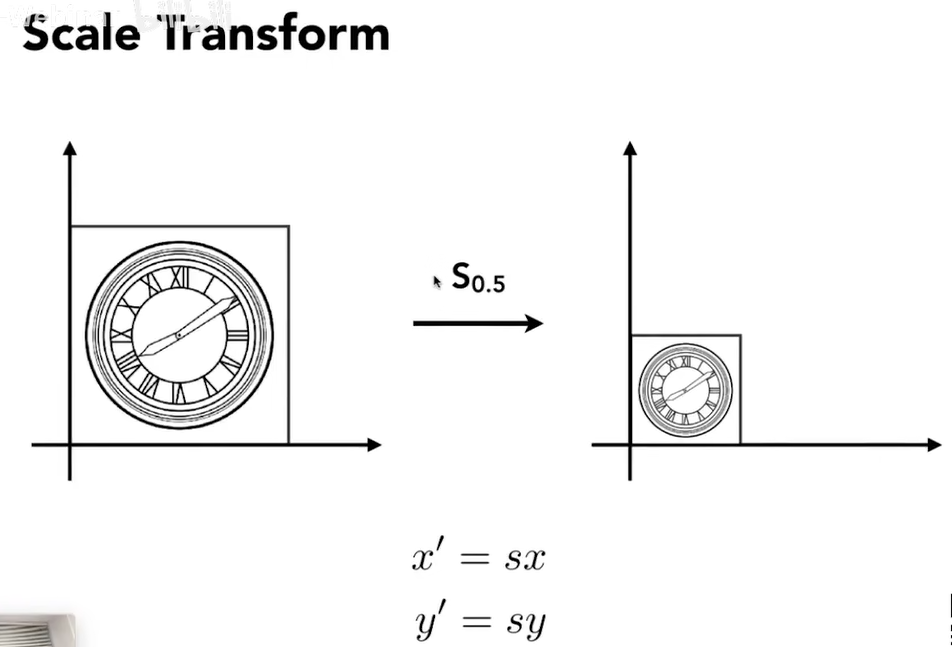
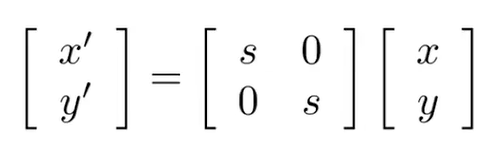其中这个对角矩阵是缩放矩阵

Reflection 反转

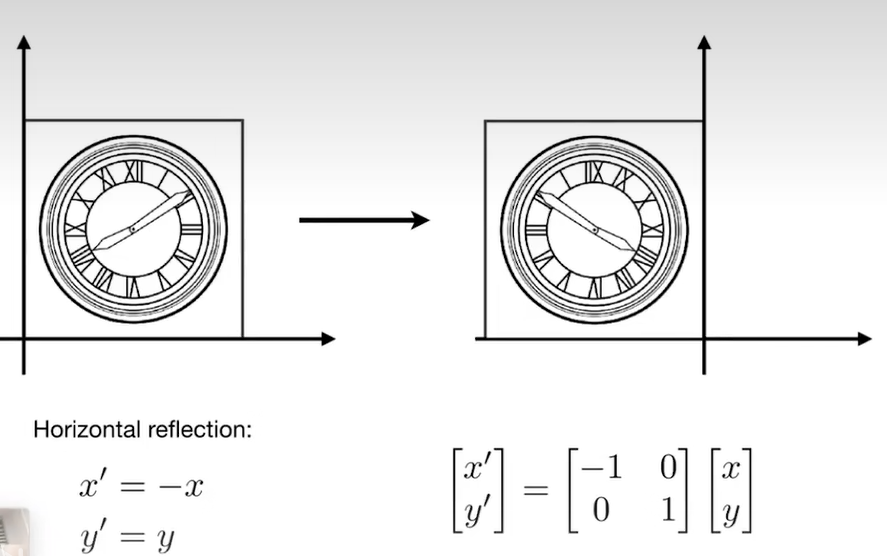
Shear 切变

Roatate 旋转

默认绕原点旋转，逆时针

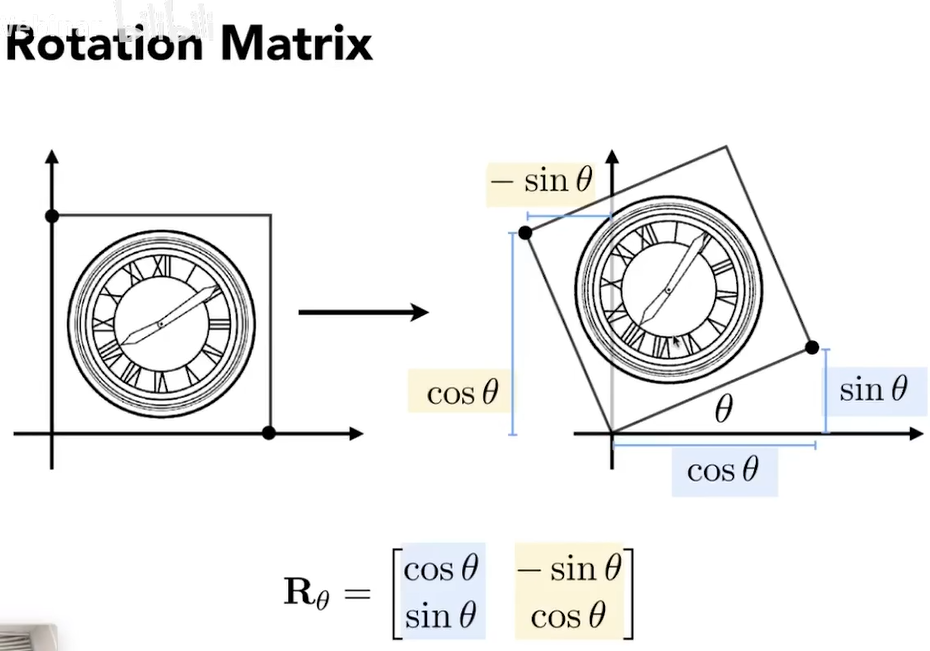
旋转-θ角是旋转θ角得到的矩阵的逆

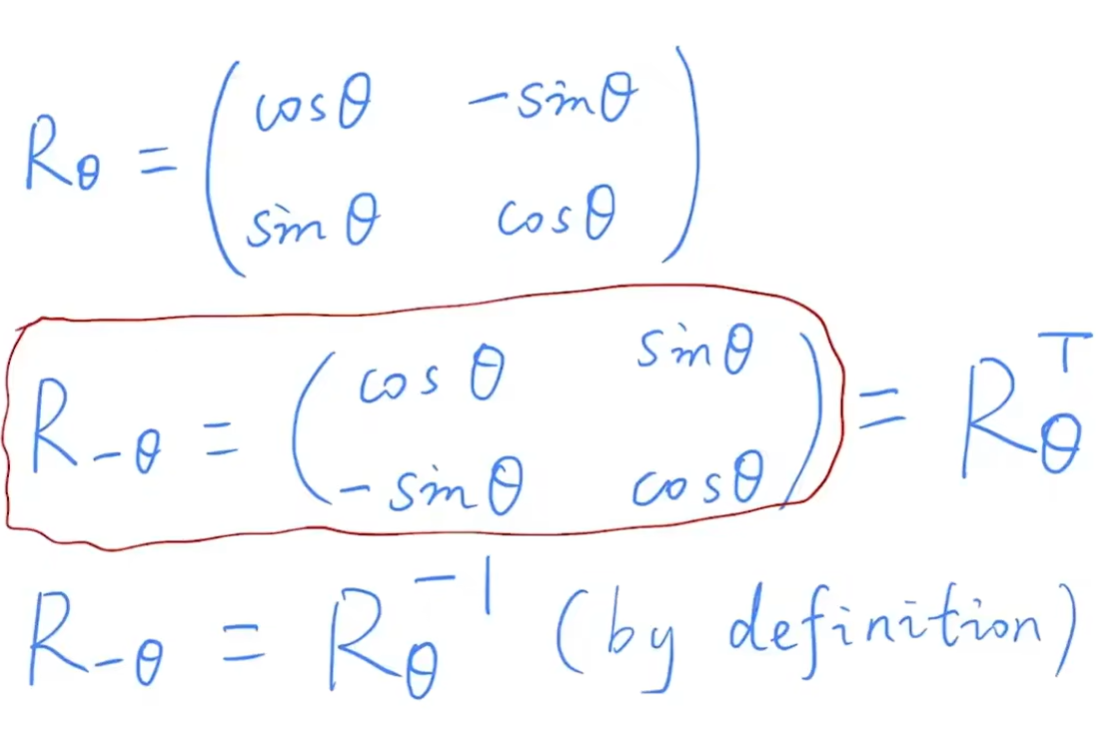
Homogeneous coordinates 齐次坐标

理由↓平移不好通过transformation操作，齐次坐标是为了把所有变换写成一个矩阵x一个向量

解决方法↓ 引入齐次方程

向量具有平移不变性！

点加点是这两个点的中点

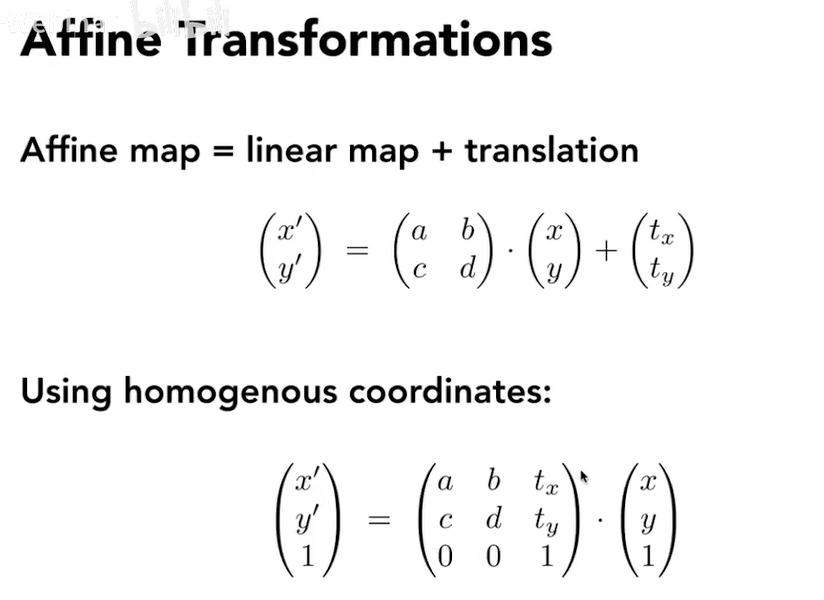
Affine Transformations 仿射变换

先应用线性变换，再平移↓

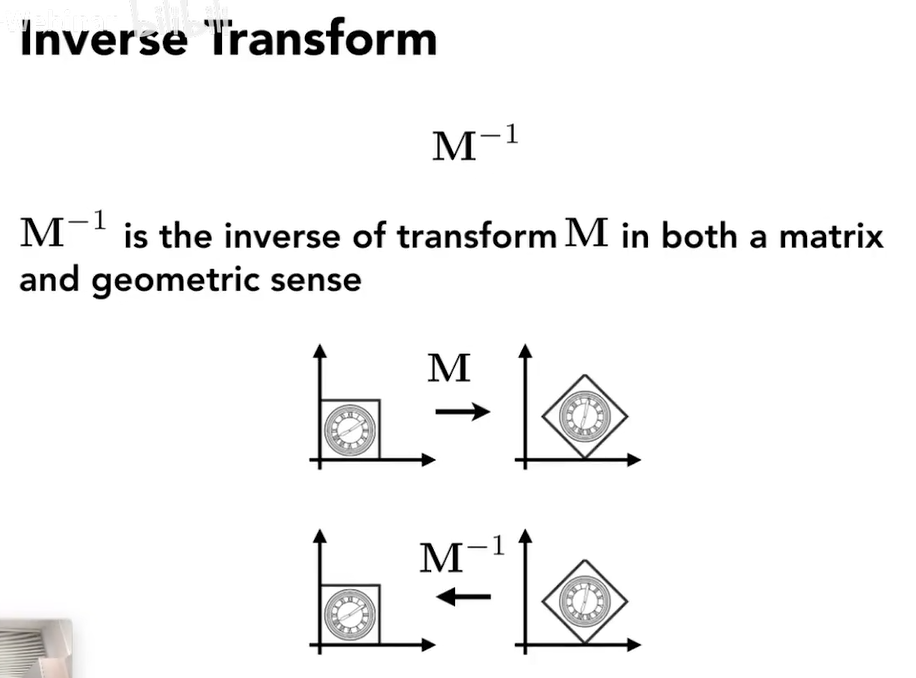
Inverse Transform 逆变换

等于乘以一个变换的逆矩阵

Composing transforms 组合变换

矩阵计算不满足交换律！

但是！矩阵有结合律！

不止能够合成！还能够分解！‘

如，想围绕某个非原点的点旋转

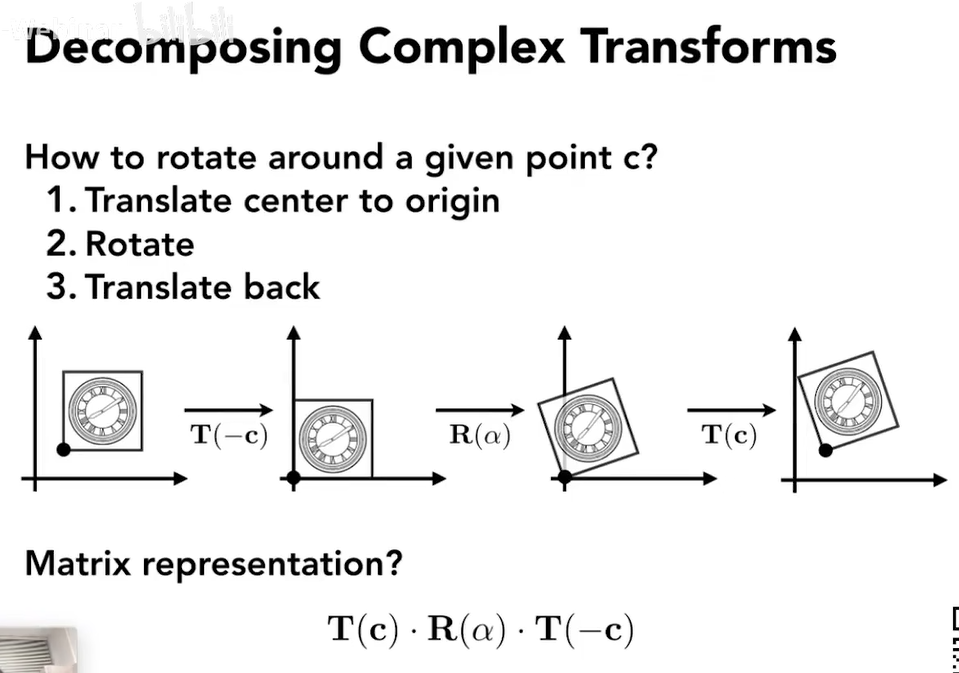
**********注意！一定要从右到左写！

3D transformations

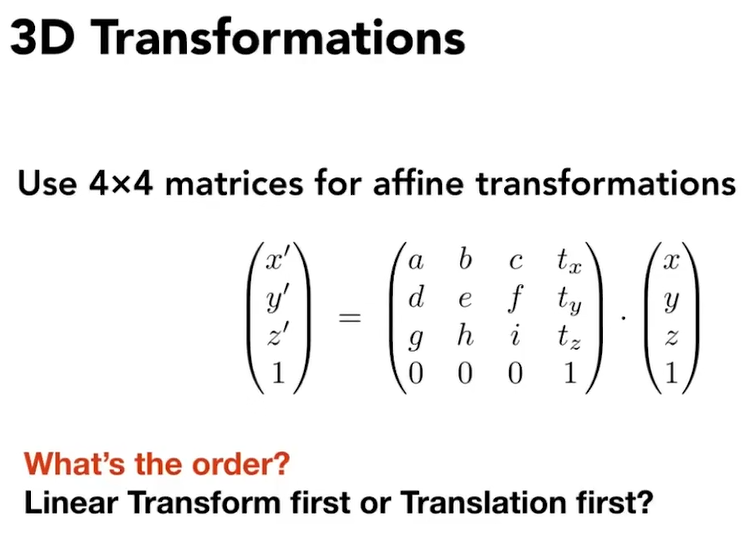
缩放和平移

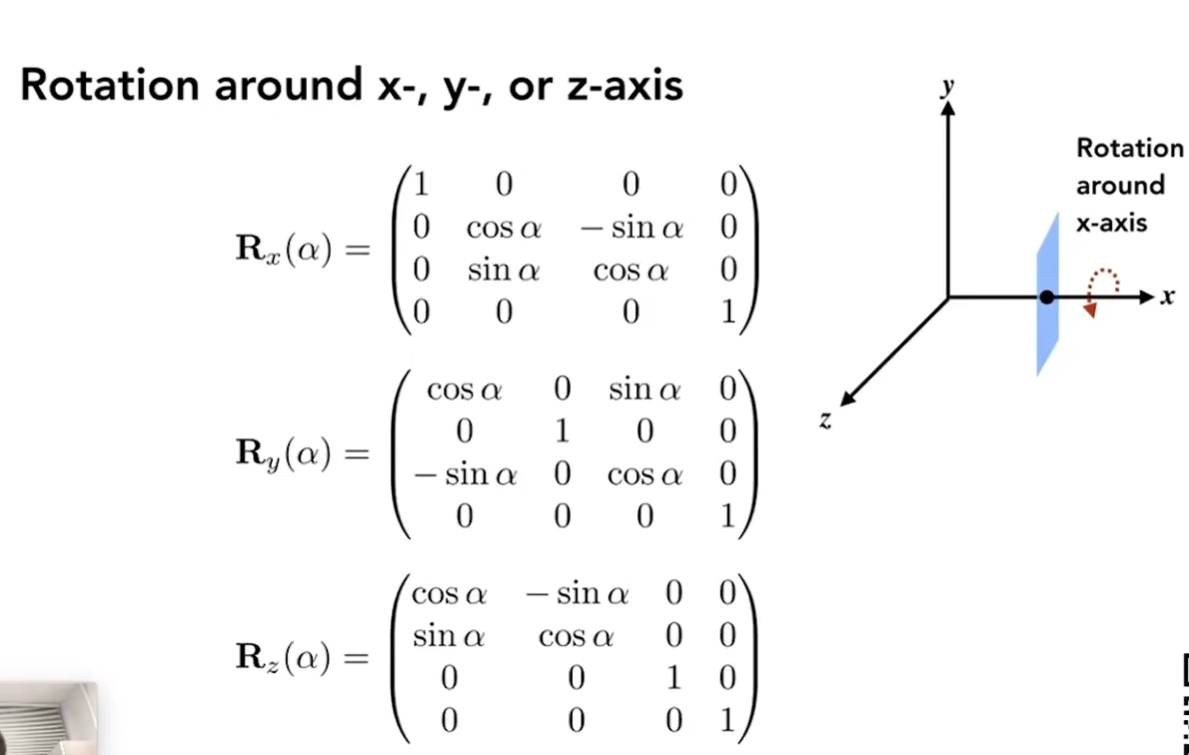
旋转

分别围绕x，y，z轴旋转，具有循环对称的性质

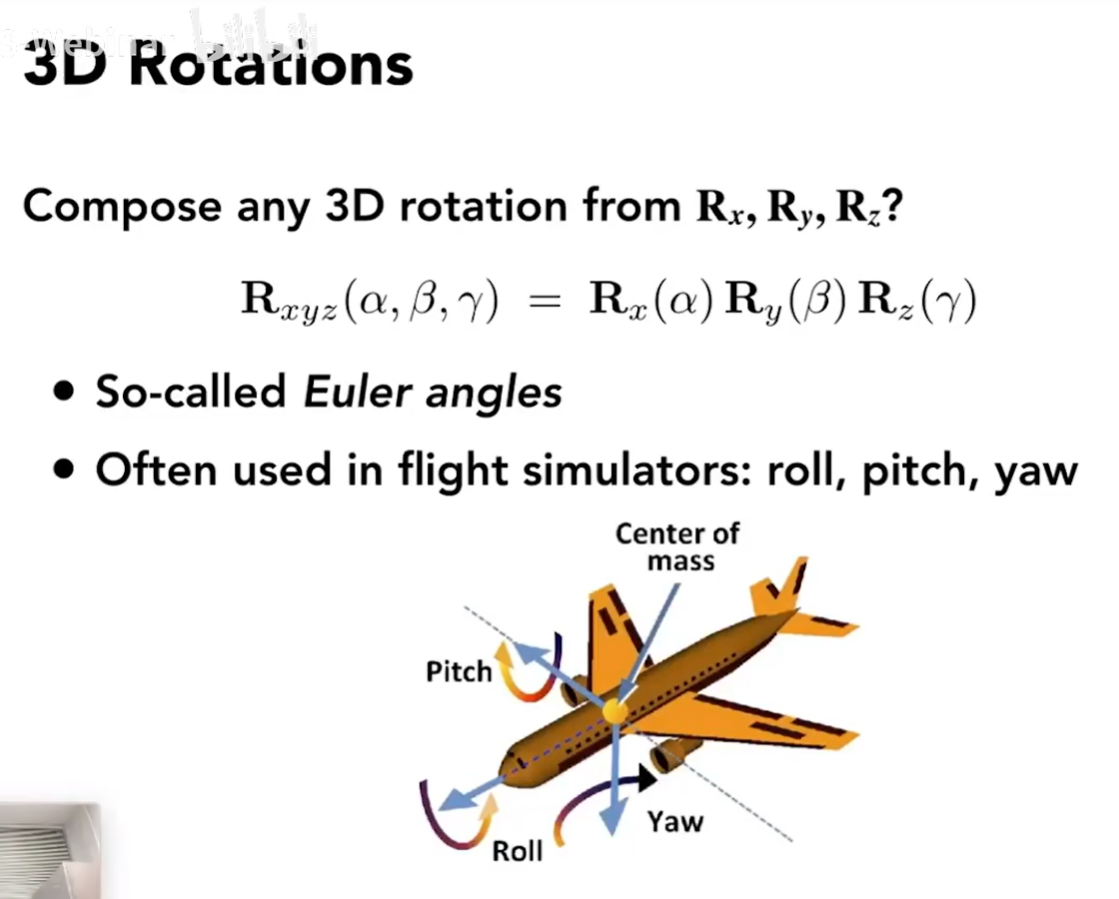
任意的旋转可以通过该矩阵合成↓

很多情况跟二维一样，都是先把图形挪到原点，旋转，再挪回去

Viewing Transformation 观测变换

View/Camera Transformation 视图变换

视图变幻可以理解为摆照相机

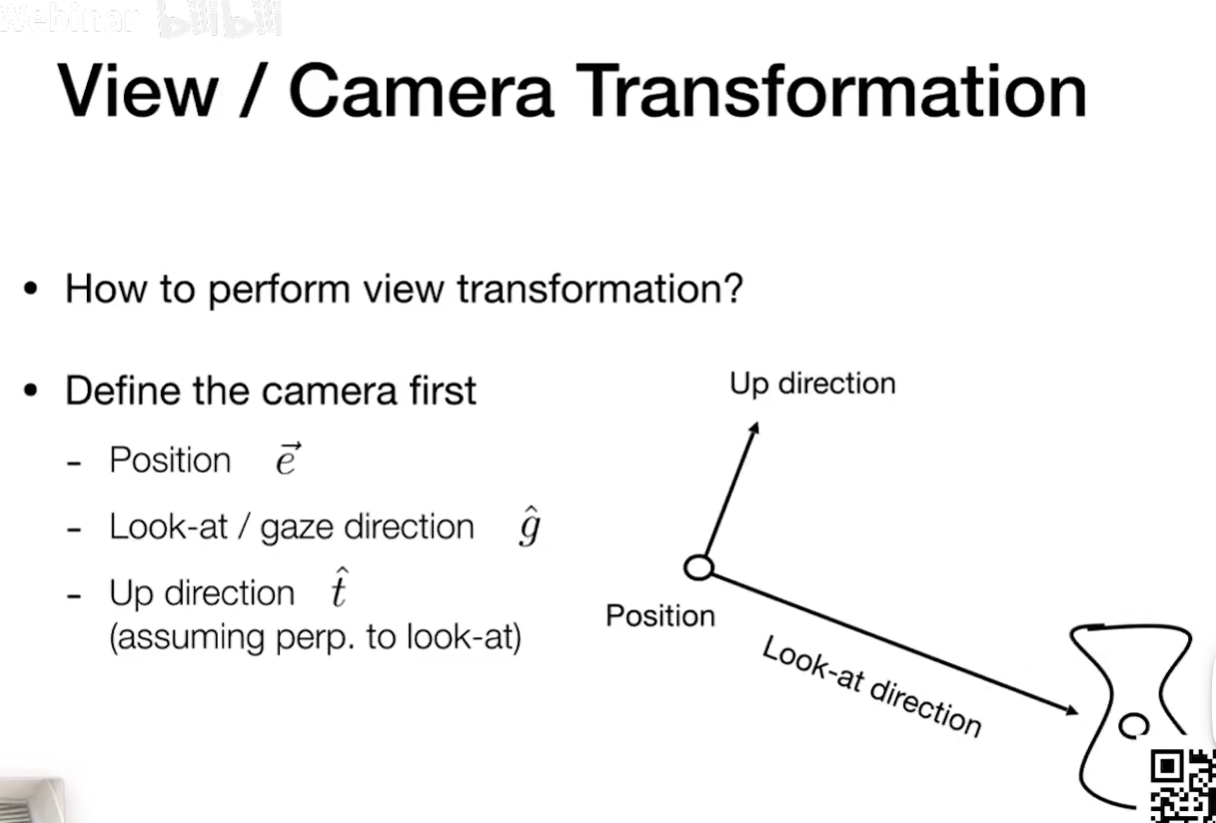
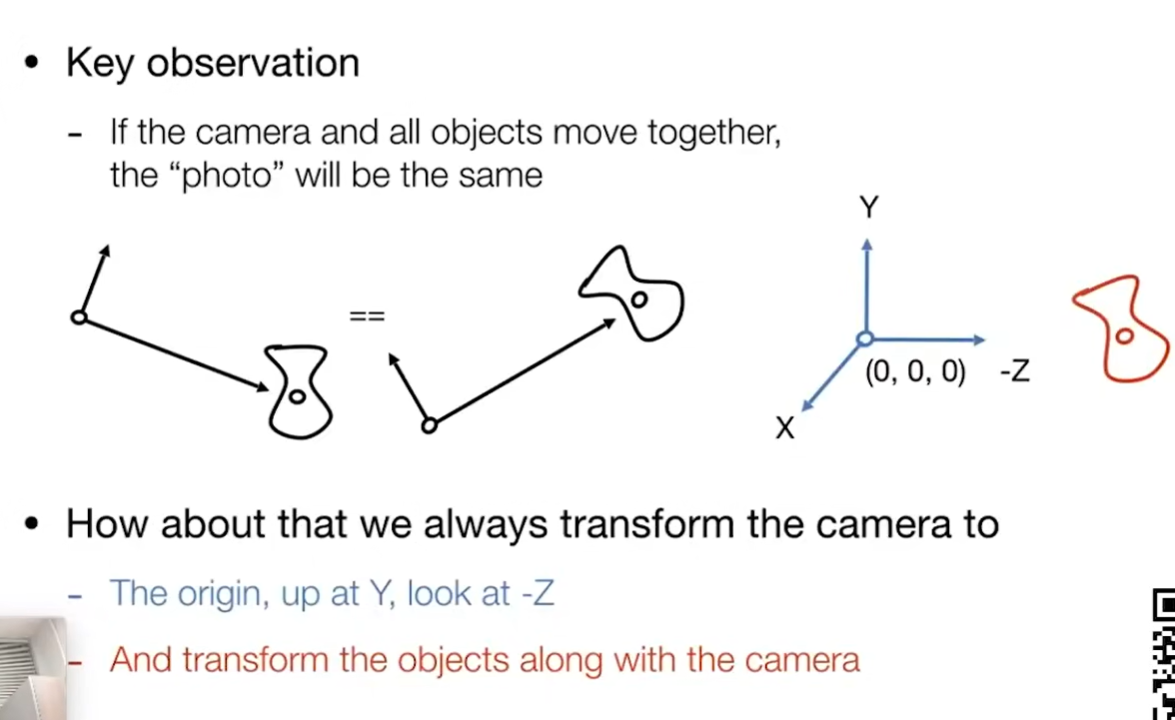
相机位置在原点，台向y，观测位置是-z轴，相机不动物体动

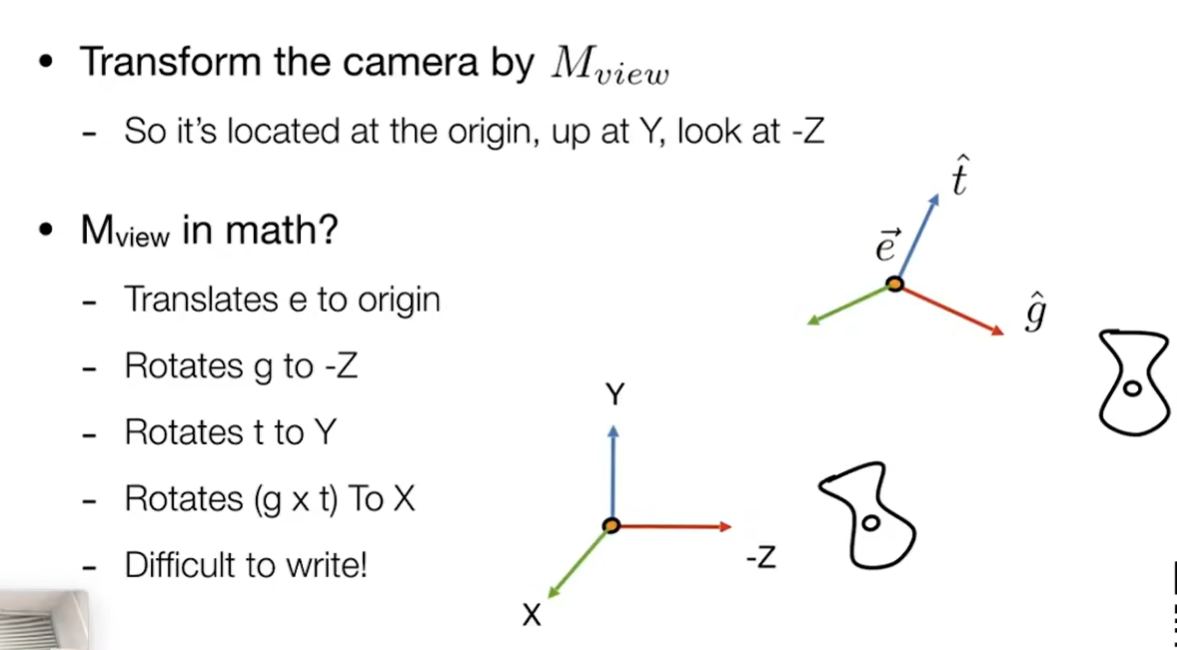
原始旋转不好求的时候求逆变换

Why？：旋转矩阵是正交矩阵，所以乘以转置就是了

Projection Transformation 投影变换

正交投影不会近大远小，但是透视投影会！

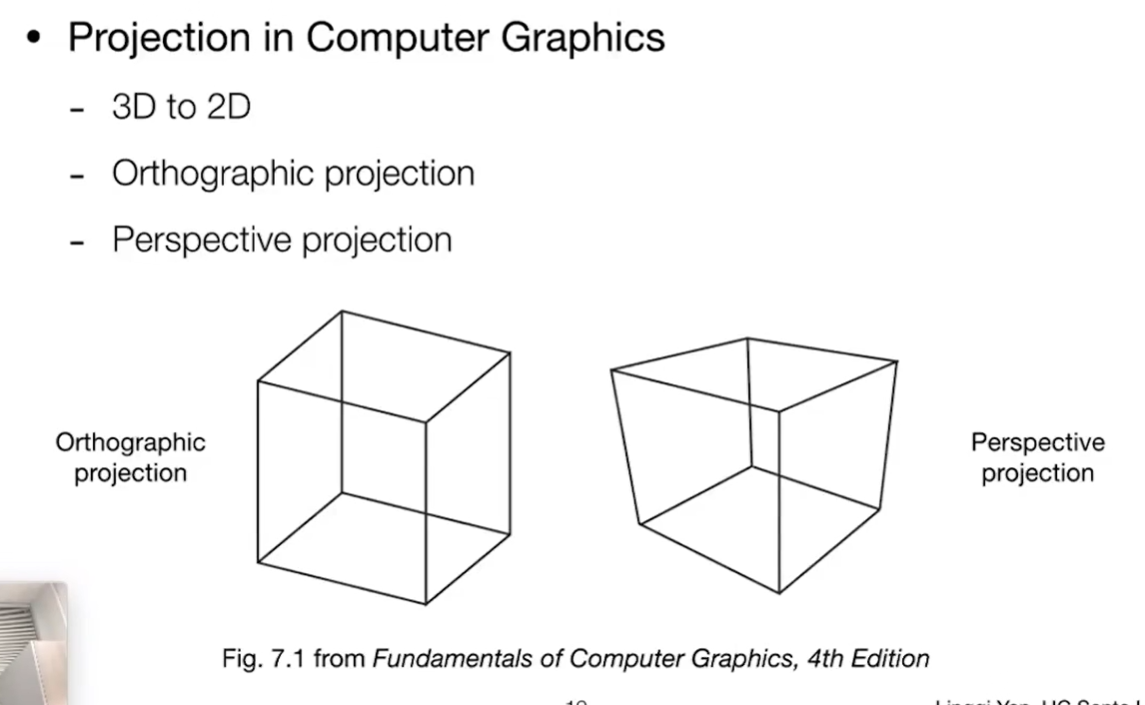
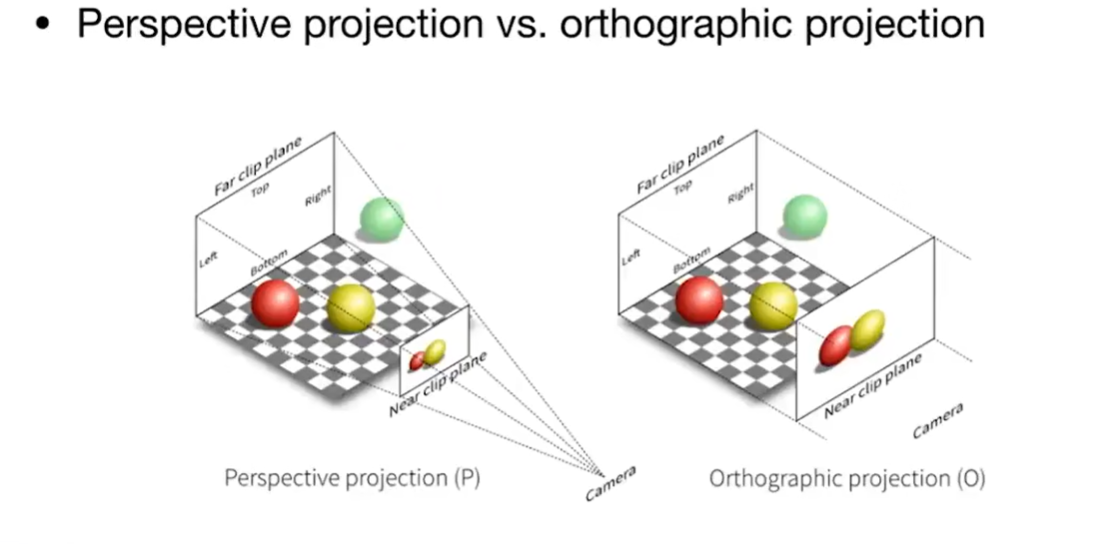
Orthographic Projection 正交投影

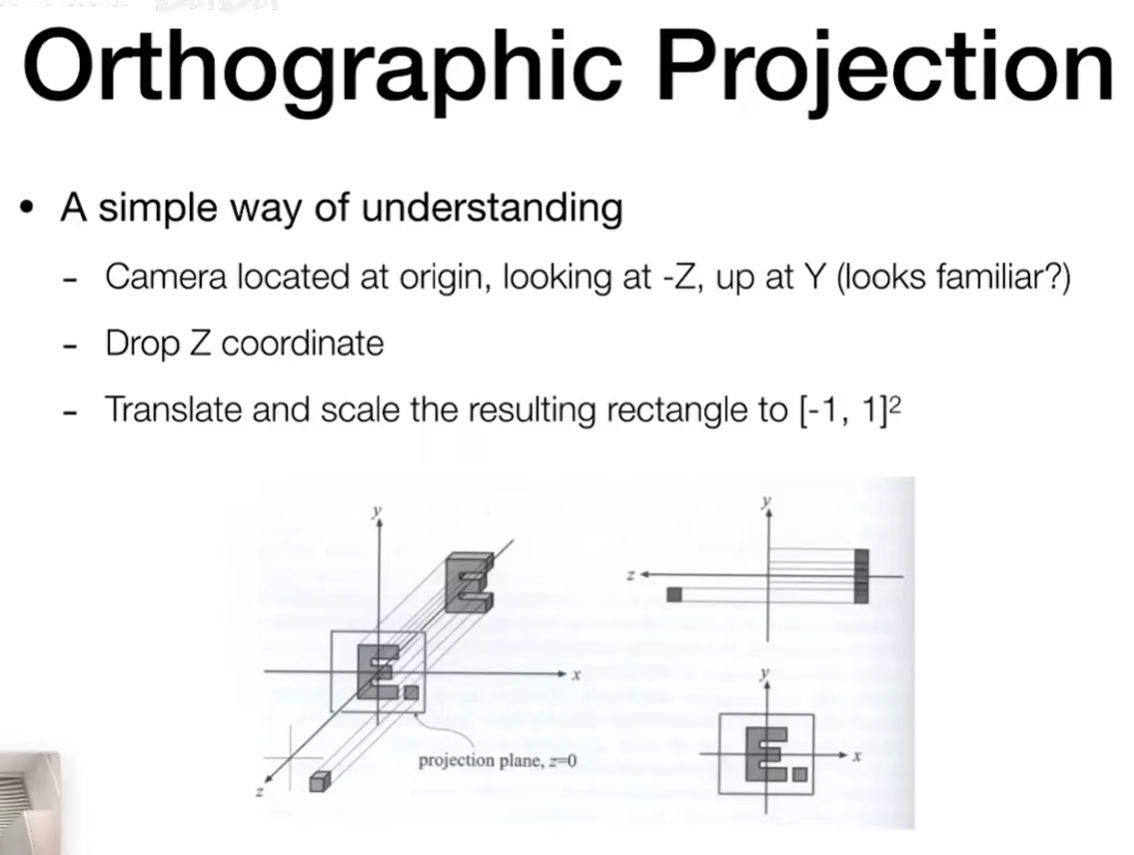
把无论怎样的长方体映射成标准的正方体

注意！因为我们是沿着负z方向看所以数值越近越大！但是opengl因为是左手系所以这里是相反的！

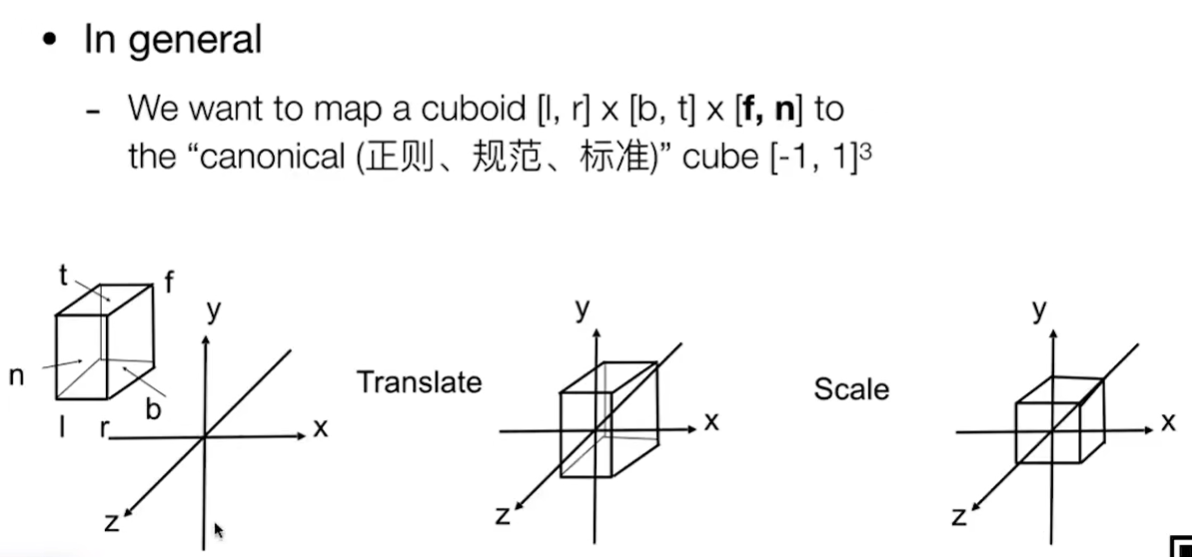
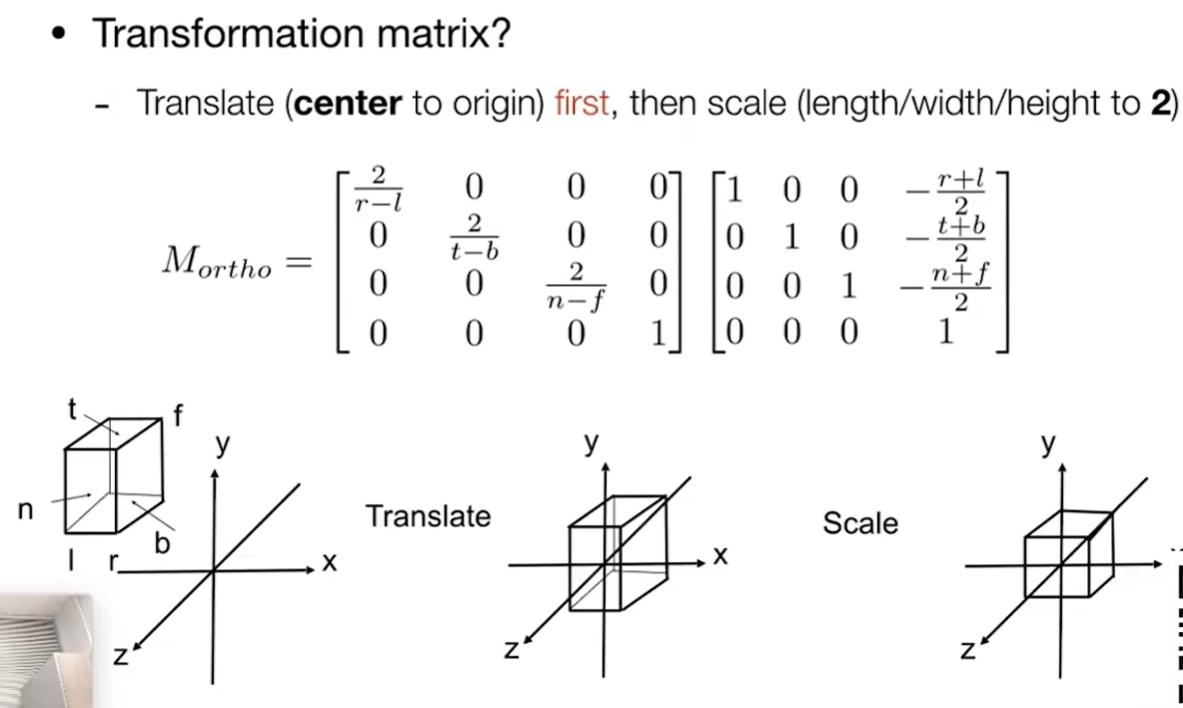
正规做法：先平移再缩放

先去左/右 上/下 前/后的中点平移到原点上，再进行缩放

Perspective Projection 透视投影

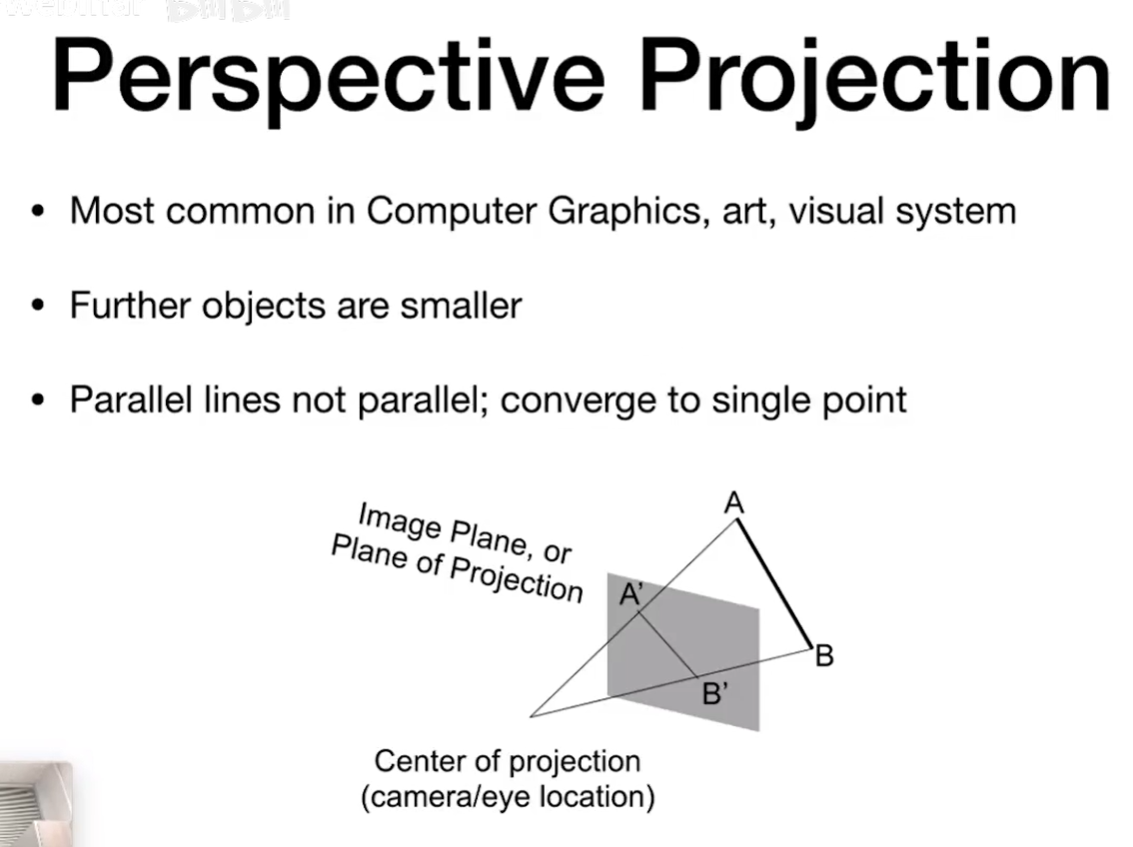
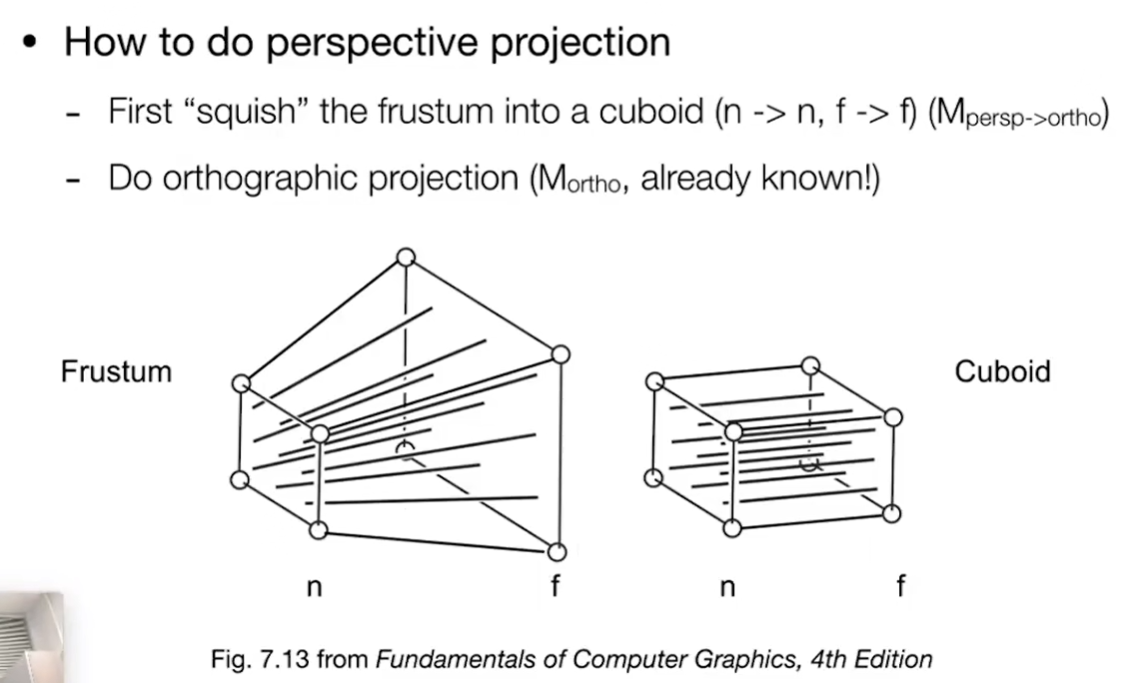
先挤压，再做正交投影

规定：近平面永远不变

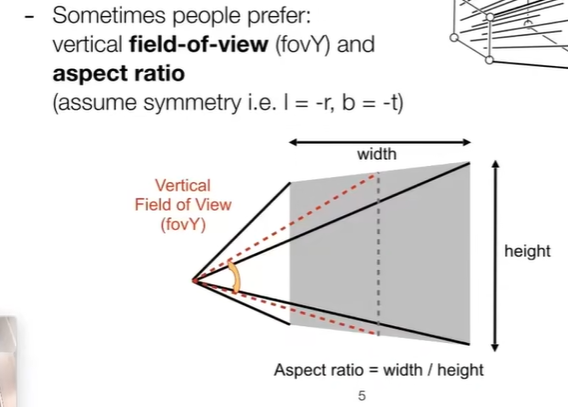
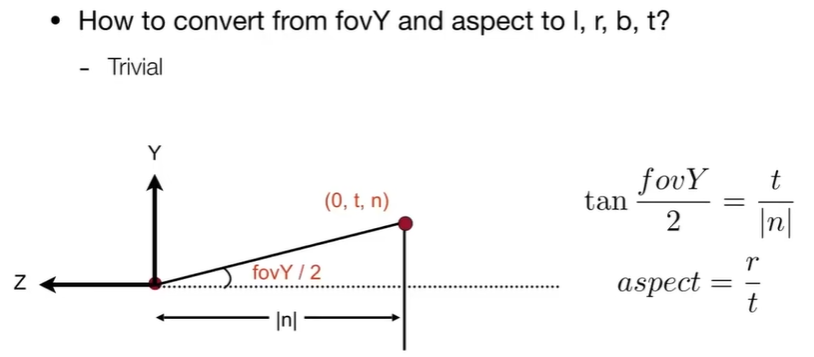
如何挤压↓通过相似三角形计算！（死去的初高中记忆开始攻击我）

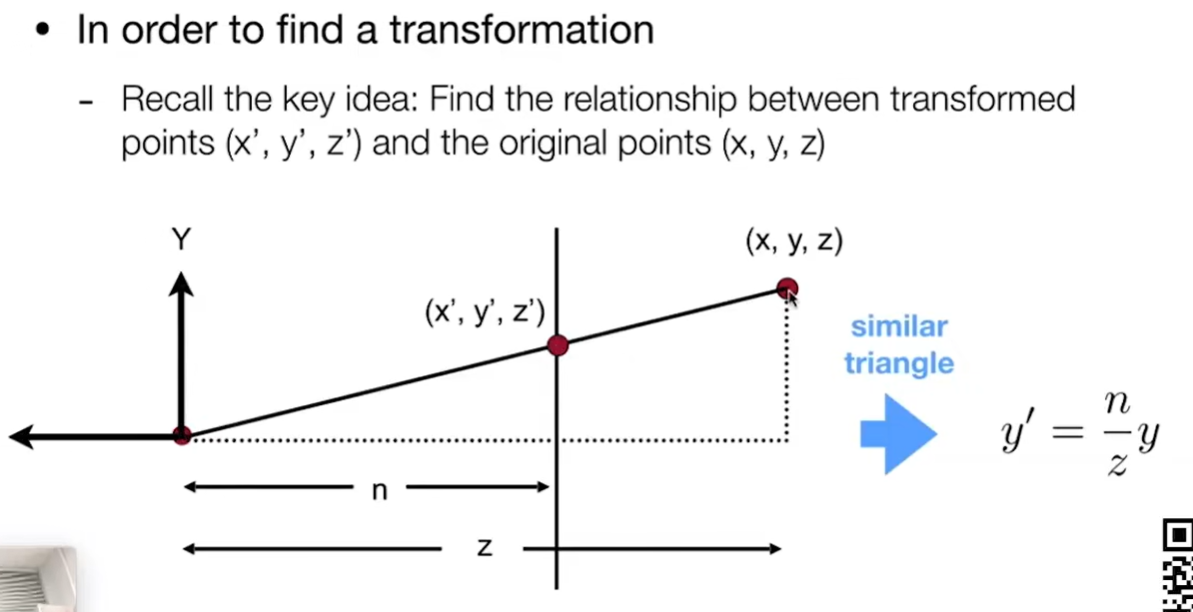
只要知道x和y怎么变化就可以推了

那z？？？？怎么办呢↓ 在近和远的地方不变！

​​​​​​​