本文介绍了Python标准库heapq模块，它用于实现堆数据结构，特别是最小堆，常用于优先队列。heapq提供了heapify、heappush、heappop、heappushpop和heapreplace等函数，用于在列表上执行堆操作，具有O(log n)的时间复杂度，适用于需要高效访问最小元素的场景。此外，还展示了如何利用heapq进行堆排序和寻找最大/小元素。
Python中的heapq优先队列
heapq 模块是 Python 标准库中用于堆（heap）数据结构的工具，一种轻量级的方式来实现优先队列（Priority Queue），也称为最小堆（Min-Heap）。优先队列是一种特殊的队列，其中每个元素都关联有一个优先级或权重，并且具有最高优先级（最小权重）的元素始终位于队列的前面。它提供了一组函数，用于在列表上执行堆操作，通常用于实现优先队列和与优先级相关的算法。
如下图，是一个heapq优先队列二叉树结构：
01
原理和特点
原理
-
堆数据结构：堆是一种特殊的树状数据结构，通常用于实现优先队列。在最小堆中，父节点的值小于或等于其子节点的值。在最大堆中，父节点的值大于或等于其子节点的值。
-
二进制堆：
heapq模块实现的是二进制堆，这是一种紧凑的数据结构，通常以列表的形式表示。它的性质是：父节点的索引i与其左子节点的索引2i+1和右子节点的索引2i+2之间存在特定的关系。
特点
在 heapq 中，优先队列的实现依赖于堆数据结构，因此它具有以下特点：
-
最小堆性质
在优先队列中，具有最高优先级的元素（最小权重）始终位于队列的前面，因此可以轻松地获取并移除具有最高优先级的元素。
-
高效性能
堆是一种高效的数据结构，插入和删除元素的时间复杂度为 O(log n)，其中 n 是队列中元素的数量。这使得优先队列非常适合需要快速访问最高优先级元素的应用。
02
常见用法
heapq.heapify(iterable) 堆排序
使用 heapify(iterable) 函数，可以将一个可迭代对象（通常是列表）转换为堆。这个函数在原地进行操作，不返回新的堆对象。
import heapq
numbers = [34, 25, 12, 99, 87, 63, 58, 78, 88, 92]
print(f'转换前的列表: {numbers}') # 转换前的列表: [34, 25, 12, 99, 87, 63, 58, 78, 88, 92]
# 将列表转换成堆序列，不返回数据
heapq.heapify(numbers)
print(f'转换后的列表: {numbers}') # 转换后的列表: [12, 25, 34, 78, 87, 63, 58, 99, 88, 92]
转换后的堆序列：
headpq.heappush(heap, item) 插入元素
使用 heappush(heap, item) 函数，可以将元素推入堆。
import heapq
numbers = [34, 25, 12, 99, 87, 63, 58, 78, 88, 92]
print(f'转换前的列表: {numbers}') # 转换前的列表: [34, 25, 12, 99, 87, 63, 58, 78, 88, 92]
# 将列表转换成堆序列，不返回数据
heapq.heapify(numbers)
print(f'转换后的列表: {numbers}') # 转换后的列表: [12, 25, 34, 78, 87, 63, 58, 99, 88, 92]
# 插入元素
heapq.heappush(numbers, 30)
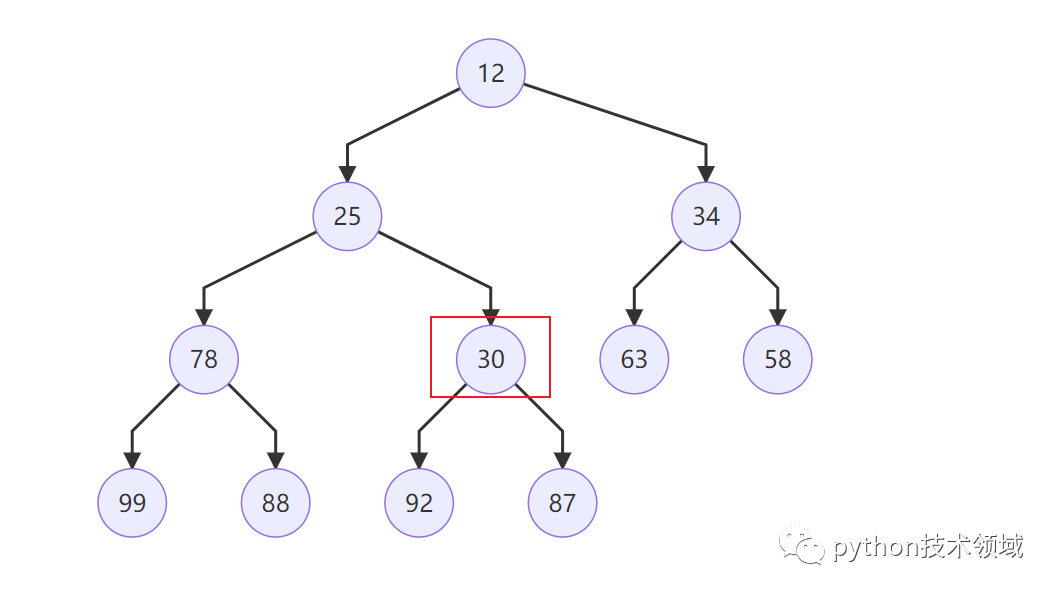
print(f'插入元素后的列表: {numbers}') # 插入元素后的列表: [12, 25, 34, 78, 30, 63, 58, 99, 88, 92, 87]
插入元素后的堆序列：
heapq.heappop(heap) 弹出最小元素
使用 heappop(heap) 函数，可以从堆中弹出并返回最小的元素。
import heapq
numbers = [34, 25, 12, 99, 87, 63, 58, 78, 88, 92]
print(f'转换前的列表: {numbers}') # 转换前的列表: [34, 25, 12, 99, 87, 63, 58, 78, 88, 92]
# 将列表转换成堆序列，不返回数据
heapq.heapify(numbers)
print(f'转换后的列表: {numbers}') # 转换后的列表: [12, 25, 34, 78, 87, 63, 58, 99, 88, 92]
# 弹出最小元素
heapq.heappop(numbers)
print(f'弹出最小元素后的列表: {numbers}') # 弹出最小元素后的列表: [25, 78, 34, 88, 87, 63, 58, 99, 92]
弹出最小元素后的堆序列：
heapq.heappushpop(heap, item) 先推入后弹出
使用 heappushpop(heap, item) 函数，可以将元素推入堆，然后弹出并返回堆中的最小元素。这样可以减少一次堆操作。
import heapq
numbers = [34, 25, 12, 99, 87, 63, 58, 78, 88, 92]
print(f'转换前的列表: {numbers}') # 转换前的列表: [34, 25, 12, 99, 87, 63, 58, 78, 88, 92]
# 将列表转换成堆序列，不返回数据
heapq.heapify(numbers)
print(f'转换后的列表: {numbers}') # 转换后的列表: [12, 25, 34, 78, 87, 63, 58, 99, 88, 92]
# 插入并弹出最小元素
heapq.heappushpop(numbers, 0)
print(f'插入后弹出最小元素后的列表: {numbers}') # 插入后弹出最小元素的列表: [12, 25, 34, 78, 87, 63, 58, 99, 88, 92]
插入并弹出最小元素后的堆序列：
heapq.heapreplace(heap, item) 先弹出后替换
使用 heapreplace(heap, item) 函数，可以弹出并返回堆中的最小元素，然后将新元素推入堆。这样也可以减少一次堆操作。
import heapq
numbers = [34, 25, 12, 99, 87, 63, 58, 78, 88, 92]
print(f'转换前的列表: {numbers}') # 转换前的列表: [34, 25, 12, 99, 87, 63, 58, 78, 88, 92]
# 将列表转换成堆序列，不返回数据
heapq.heapify(numbers)
print(f'转换后的列表: {numbers}') # 转换后的列表: [12, 25, 34, 78, 87, 63, 58, 99, 88, 92]
# 先弹出最小值后插入值
heapq.heapreplace(numbers, 0)
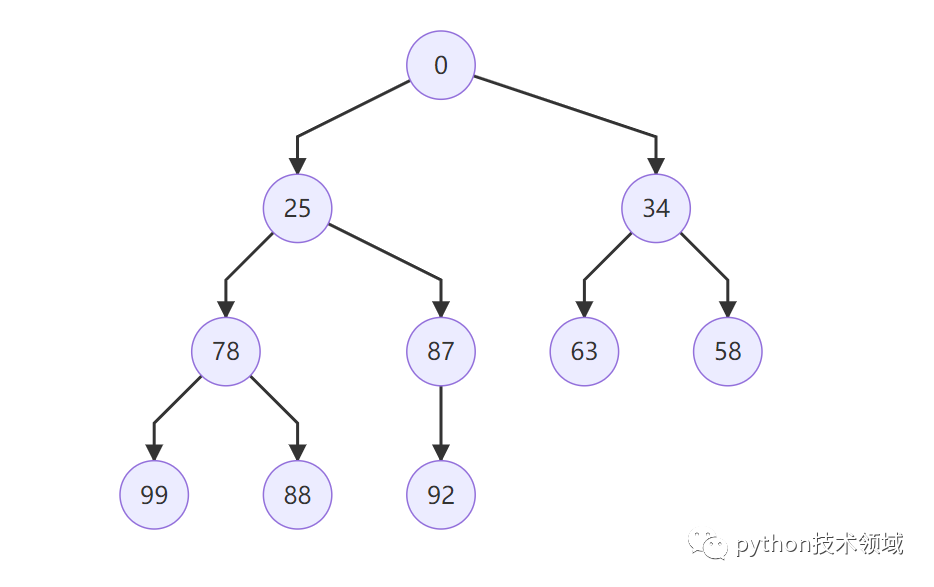
print(f'弹出最小值后插入值后的列表: {numbers}') # 插入后弹出最小元素后的列表: [0, 25, 34, 78, 87, 63, 58, 99, 88, 92]
先弹出最小值后插入值后的堆序列：
利用堆排序找最大最小的N个元素
heapq 模块还包括其他一些有用的函数，用于堆操作，例如查找最大的 N 个元素、合并多个有序堆等。这些函数使 heapq 成为处理优先队列和类似问题的强大工具。堆的性质使得它在需要高效访问最小/最大元素的场景中非常有用，如调度算法、任务排程、图算法等。
案例：
"""
从列表中找出最大的或最小的N个元素
堆结构(大根堆/小根堆)
"""
import heapq
numbers = [34, 25, 12, 99, 87, 63, 58, 78, 88, 92]
list2 = [
{"product": "手机", "cost_price": 500, "selling_price": 699},
{"product": "电视", "cost_price": 800, "selling_price": 999},
{"product": "笔记本电脑", "cost_price": 1000, "selling_price": 1299},
{"product": "平板电脑", "cost_price": 300, "selling_price": 399},
{"product": "耳机", "cost_price": 30, "selling_price": 49},
{"product": "键盘鼠标套装", "cost_price": 40, "selling_price": 69}
]
# 最大的 3个 元素
print(heapq.nlargest(3, numbers))
# 最小的 3个 元素
print(heapq.nsmallest(3, numbers))
# 成本价格最大的 2个 元素
print(heapq.nlargest(2, list2, key=lambda x: x['cost_price']))
# 销售价格最大的 2个 元素
print(heapq.nlargest(2, list2, key=lambda x: x['selling_price']))
执行结果：
题外话
感兴趣的小伙伴，赠送全套Python学习资料，包含面试题、简历资料等具体看下方。
👉优快云大礼包🎁：全网最全《Python学习资料》免费赠送🆓！（安全链接，放心点击）
一、Python所有方向的学习路线
Python所有方向的技术点做的整理，形成各个领域的知识点汇总，它的用处就在于，你可以按照下面的知识点去找对应的学习资源，保证自己学得较为全面。
二、Python必备开发工具
工具都帮大家整理好了，安装就可直接上手！
三、最新Python学习笔记
当我学到一定基础，有自己的理解能力的时候，会去阅读一些前辈整理的书籍或者手写的笔记资料，这些笔记详细记载了他们对一些技术点的理解，这些理解是比较独到，可以学到不一样的思路。
四、Python视频合集
观看全面零基础学习视频，看视频学习是最快捷也是最有效果的方式，跟着视频中老师的思路，从基础到深入，还是很容易入门的。
五、实战案例
纸上得来终觉浅，要学会跟着视频一起敲，要动手实操，才能将自己的所学运用到实际当中去，这时候可以搞点实战案例来学习。
六、面试宝典
简历模板
👉优快云大礼包🎁：全网最全《Python学习资料》免费赠送🆓！（安全链接，放心点击）
若有侵权，请联系删除
扫一扫
1万+
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
