题目:哈夫曼编码
背景:
哈夫曼编码是一种被广泛应用而且非常有效的数据压缩编码,它是可变长度编码。可变长编码即可以对待处理字符串中不同字符使用不等长的二进制位表示,可变长编码比固定长度编码好很多,可以对频率高的字符赋予短编码,而对频率较低的字符则赋予较长一些的编码,从而可以使平均编码长度减短,起到压缩数据的效果。
哈夫曼编码是前缀编码。如果没有一个编码是另一个编码的前缀,则称这样的编码为前缀编码。对前缀编码的解码也是相对简单的,因为没有一个码是另一个编码的前缀,所以可以识别出第一个编码,将它翻译为原码,再对余下的编码文件重复同样操作。
哈夫曼编码首先要构造一棵哈夫曼树,首先,将每个出现的字符当做一个独立的结点,其权值作为它出现的频度(或次数),然后构造哈夫曼树。显然所有字符节点均出现在叶子结点中。我们可以将字符的编码解释为从根至该字符路径上标记的序列,其中标记为0表示"转向左孩子",标记为1表示为"转向右孩子"。
#include<stdio.h>
#include<malloc.h>
#include<iostream>
#include<stdlib.h>
#include<string.h>
#define max 10
#define max2 1000
using namespace std;
typedef struct{ //哈夫曼树
int weight; //存放权重
int parent,lchild,rchild;
char code[max]; //哈夫曼编码
char ch; //字母
}huff;
char encode[15];char dcode[max];
void inithuff(huff *H,int *w,char *z,int n){
int i;
for(i=0;i<n*2-1;i++){
H[i].ch=z[i];
H[i].weight=w[i];
H[i].parent=-1;
H[i].lchild=-1;
H[i].rchild=-1;
}
}
void gethuff(huff *H,int n){
int x1,x2;
int m1,m2;
int i,j;
for(i=n;i<2*n-1;i++){
x1=x2=0;
m1=m2=max2;
for(j=0;j<i;j++){
if(H[j].parent==-1&&H[j].weight<m1){
m2=m1;
x2=x1;
m1=H[j].weight;
x1=j;
}
else if(H[j].parent==-1&&H[j].weight<m2){
m2=H[j].weight;
x2=j;
}
}
H[x1].parent=i;
H[x2].parent=i;
H[i].lchild=x1;
H[i].rchild=x2;
H[i].weight=m1+m2;
}
}
void bmhuff(huff *H,int n){
FILE *fp1;
char t[max];
int i,j,k,p,parent;
int g=0;
int len; //记录编码长度
for(i=0;i<n;i++){
len=0;
parent=H[i].parent; //储存双亲结点下表
p=i; //用p来更新孩子的下标
while(parent!=-1){ //没到根节点
if(H[parent].lchild==p){ //左孩子
t[len]='0';len++;
}
else if(H[parent].rchild==p){
t[len]='1';len++;
}
p=parent; //更新孩子以及双亲下表
parent=H[parent].parent;
}
for(j=0,k=len-1;j<len;j++,k--) //将反向的编码调正
H[i].code[j]=t[k];
H[i].code[j]='\0'; //结束符
for(j=0;j<len;j++){
encode[g]=H[i].code[j];
g++;
}
}
encode[g]='\0';
fp1=fopen("code1.txt","w");
fprintf(fp1,"%s",encode);
fclose(fp1);
}
void ymhuff(huff *H,char *code,int n){ //译码
int i,j=0;
int k=0;
FILE *fp2;
i=2*n-2;
while (code[j] != '\0')
{
if (code[j] == '0') //如果为'0',则指向其左孩子
i = H[i].lchild;
else if (code[j] == '1') //如果为'1',则指向其左孩子
i = H[i].rchild;
if (H[i].lchild == -1) //直到叶子节点
{
dcode[k]=H[i].ch;
k++;
i = 2*n-2;
}
j++; //再读下一个字符
}
fp2=fopen("code2.txt","w");
fprintf(fp2,"%s",dcode);
fclose(fp2);
}
void print(huff *H,int n){
int i,t;
for(i=0;i<n*2-1;i++){
printf("%d %d %d %d",i,H[i].lchild,H[i].rchild,H[i].parent);
printf("\n");
}
}
int main(){
int i,n,a; //n为叶子个数
char *z,Z; //存放字母
int w[max],W; //存放权重
huff H[max];
printf("请输入叶子个数:");
scanf("%d",&n);
printf("菜单:输入1编码,2译码, 3展示,4退出:\n");
for(int j=0;;j++){
printf("请输入:");
scanf("%d",&a);
if(a==1){
z=(char*)malloc(n*sizeof(char));
for(i=0;i<n;i++)
{
printf("请输入第%d个字符:",i+1);
cin>>z[i];
printf("请输入第%d个字符的权:",i+1);
cin>>w[i];
}
inithuff(H,w,z,n);
gethuff(H,n);
bmhuff(H,n);
for(i=0;i<n;i++){
printf("%c:%s ",H[i].ch,H[i].code);
}
printf("\n");
printf("完整编码为:%s\n",encode);
}
else if(a==2){
ymhuff(H,encode,n);
printf("译码后:%s\n",dcode);
printf("\n");
}
else if(a==3){
printf("i lc rc p\n");
print(H,n);
}
else{
exit(0);
}
}
return 0;
}
运行结果及分析:
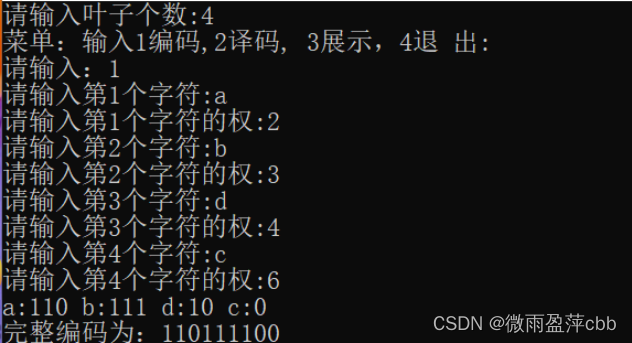
1编码,输入叶子节点对应的字母和权值,进行编码

2译码,将编码翻译成字母。
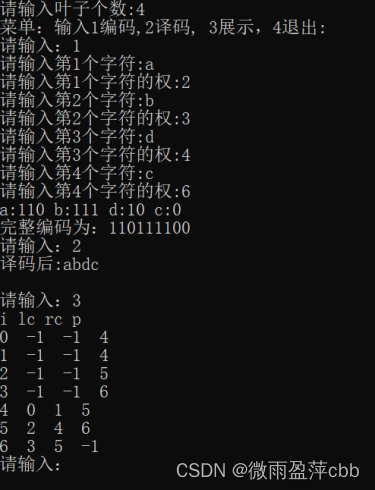
3对树进行展示
本文介绍了数据结构作业---哈夫曼树,欢迎大家评论关注。























 3133
3133

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










