拓扑排序

拓扑排序（Toplogical Sort）从一组有依赖关系的任务中得到一个能完成所有任务的序列。

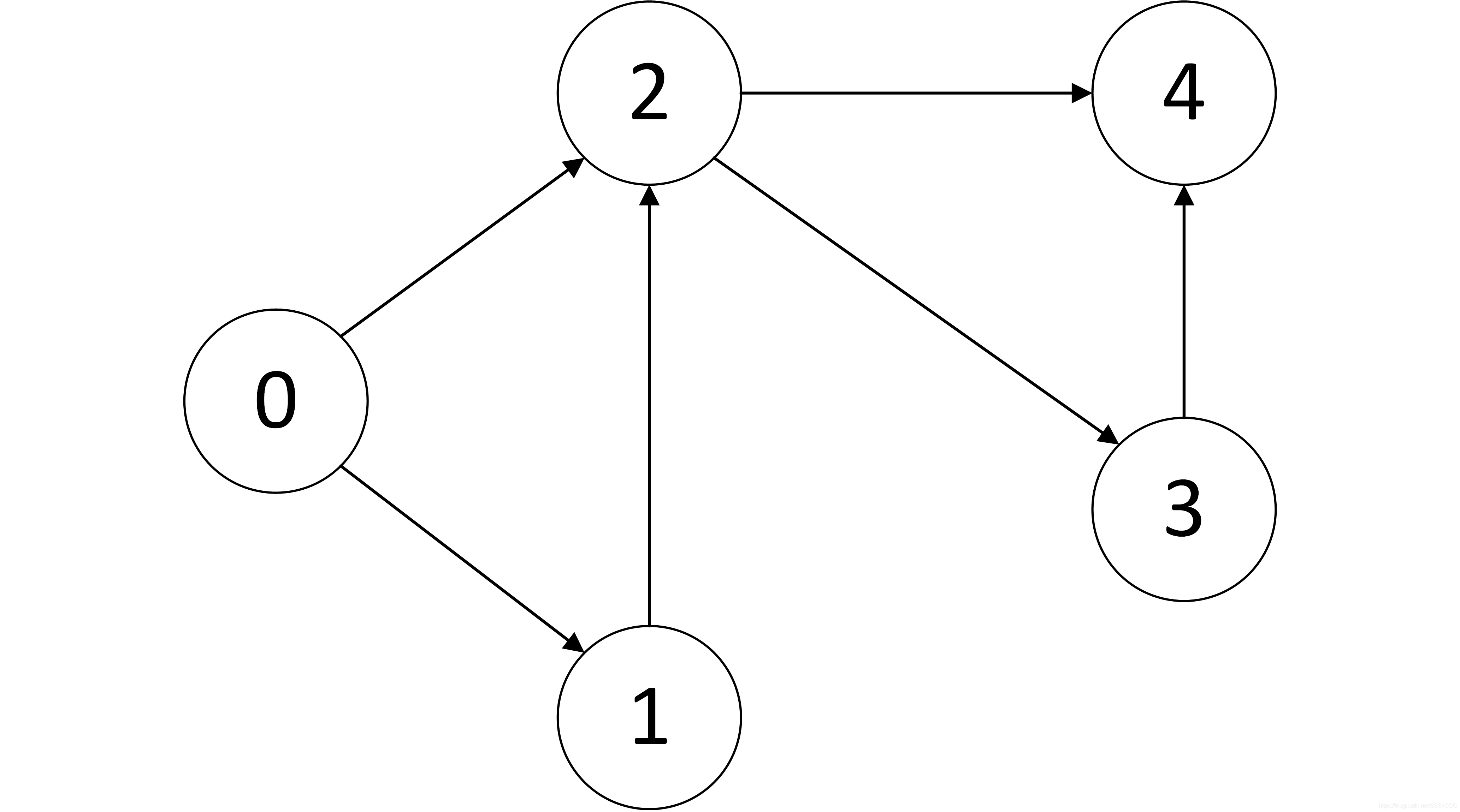
如图所示，有5个任务：0、1、2、3、4。其中有依赖关系：

0必须在1和2之前完成；

1必须在2之前完成；

2必须在3和4之前完成；

3必须在4之前完成。

这样一组有依赖关系的任务可以看成是一个有向图，其中图的顶点是任务，有向边是依赖关系。

根据此图一个能完成所有任务的序列是：0 -> 1 -> 2 -> 3 -> 4。

排序算法步骤：

顶点的入度是指在图中终点为该顶点的边的数量。

1 初始化排序结果为一个空的列表

2 选取入度为0的顶点加到排序结果列表的最后

3 在图中删除这个顶点，如果所有顶点都从图中删除了则结束，否则回到步骤2

java代码实现：

import java.util.*;

public class TopologicalSort {

    public static List<Integer> topologicalSort(Map<Integer, List<Integer>> graph) {
        Map<Integer, Integer> inDegree = new HashMap<>();
        for (List<Integer> toList : graph.values()) {
            for (int v : toList) inDegree.put(v, inDegree.getOrDefault(v, 0) + 1);
        }
        List<Integer> open = new ArrayList<>();
        for (int v : graph.keySet()) if (!inDegree.containsKey(v)) open.add(v);
        List<Integer> sorted = new ArrayList<>();
        while (!open.isEmpty()) {
            int v = open.remove(open.size() - 1);
            sorted.add(v);
            for (int toV : graph.get(v)) {
                inDegree.put(toV, inDegree.get(toV) - 1);
                if (inDegree.get(toV) <= 0) open.add(toV);
            }
        }
        return sorted.size() == graph.size() ? sorted : null;
    }

    public static void main(String[] args) {
        Map<Integer, List<Integer>> graph = new HashMap<>();
        graph.put(0, Arrays.asList(1, 2));
        graph.put(1, Arrays.asList(2));
        graph.put(2, Arrays.asList(3, 4));
        graph.put(3, Arrays.asList(4));
        graph.put(4, Arrays.asList());
        System.out.println(topologicalSort(graph));  // [0, 1, 2, 3, 4]
    }
}

源代码地址：https://github.com/SSSxCCC/Algorithm