【纪中】20200415

原创于 2020-04-16 20:49:51 发布 · 247 阅读

0 ·

CC 4.0 BY-SA版权

狗妈OJ 专栏收录该内容

16 篇文章

订阅专栏

纪中20200415解题报告

T1

题目描述

到了一年中Farmer John在他的草地里种草的时间了。整个农场由N块草地组成（1≤N≤10^5），方便起见编号为1…N，由N−1条双向的小路连接，每块草地都可以经过一些小路到达其他所有的草地。
Farmer John当然可以在每块草地里种不同种类的草，但是他想要使得使用的草的种类数最小，因为他用的草的种类数越多，他就需要负担更高的花费。
不幸的是，他的奶牛们对选择农场上的草表现得十分苛刻。如果两块相邻（由一条小路直接相连）的草地种了同一种草，或者即使是两块接近相邻（均可由一条小路直接连向同一块草地）的草地，那么奶牛们就会抱怨她们进餐的选择不够多样。Farmer John能做的只能是抱怨这些奶牛，因为他知道她们不能被满足的时候会制造多大的麻烦。
请帮助Farmer John求出他的整个农场所需要的最少的草的种类数。

输入

输入的第一行包含N。以下N−1行每行描述了一条小路连接的两块草地。

输出

输出Farmer John需要使用的最少的草的种类数。

样例输入

样例输出

提示

在这个简单的例子中，4块草地以一条直线的形式相连。最少需要三种草。例如，Farmer John可以用草A，B和C将草地按A - B - C - A的方式播种。

解题思路

这道题看起来像是什么深搜之类的东东，但是其实只需要20行，你值得拥有！

#include<iostream>
#include<cstdio>
using namespace std;
int n,f[100010],ans;
int main()
{
	freopen("planting.in","r",stdin);
	freopen("planting.out","w",stdout);
	cin>>n;
	for(int i=1;i<n;i++)
	{
		int a,b;
		scanf("%d%d",&a,&b);
		f[a]++;
		f[b]++;
	}
	for(int i=1;i<=n;i++)
		ans=max(ans,f[i]);
	cout<<ans+1<<endl;
}

T2

题目描述

Farmer John要开始他的冰激凌生意了！他制造了一台可以生产冰激凌球的机器，然而不幸的是形状不太规则，所以他现在希望优化一下这台机器，使其产出的冰激凌球的形状更加合理。
机器生产出的冰激凌的形状可以用一个N×N（1≤N≤1000）的矩形图案表示，例如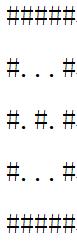：在这里插入图片描述

每个’.‘字符表示空的区域，每个’#‘字符表示一块1×1的正方形格子大小的冰激凌。
不幸的是，机器当前工作得并不是很正常，可能会生产出多个互不相连的冰激凌球（上图中有两个）。一个冰激凌球是连通的，如果其中每个冰激凌的正方形格子都可以从这个冰激凌球中其他所有的冰激凌格子出发重复地前往东、南、西、北四个方向上相邻的冰激凌格子所到达。
Farmer John想要求出他的面积最大的冰激凌球的面积和周长。冰激凌球的面积就是这个冰激凌球中’#'的数量。如果有多个冰激凌球并列面积最大，他想要知道其中周长最小的冰激凌球的周长。在上图中，小的冰激凌球的面积为2，周长为6，大的冰激凌球的面积为13，周长为22。
注意一个冰激凌球可能在中间有“洞”（由冰激凌包围着的空的区域）。如果这样，洞的边界同样计入冰激凌球的周长。冰激凌球也可能出现在被其他冰激凌球包围的区域内，在这种情况下它们计为不同的冰激凌球。例如，以下这种情况包括一个面积为1的冰激凌球，被包围在一个面积为16的冰激凌球内：
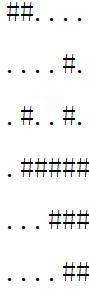
在这里插入图片描述
同时求得冰激凌球的面积和周长十分重要，因为Farmer John最终想要最小化周长与面积的比值，他称这是他的冰激凌的“冰周率”。当这个比率较小的时候，冰激凌化得比较慢，因为此时冰激凌单位质量的表面积较小。

输入

输入的第一行包含N，以下N行描述了机器的生产结果。其中至少出现一个’#'字符。

输出

输出一行，包含两个空格分隔的整数，第一个数为最大的冰激凌球的面积，第二个数为它的周长。如果多个冰激凌球并列面积最大，输出其中周长最小的那一个的信息。

样例输入

6
##....
....#.
.#..#.
.#####
...###
....##

样例输出

13 22

解题思路

这道题的正解应该是BFS，DFS在全部都是“#”的情况下会在这里插入图片描述
所以本人就很不要脸的加了个特判~

#include<iostream>
#include<cstdio>
using namespace std;
int n,a[1010][1010],b[1010][1010],c[1010][1010],hh;
const int xn[5]={0,0,0,1,-1};
const int yn[5]={0,1,-1,0,0};
int maxn,maxnn,ans,anss;
void dfs(int x,int y)
{
	ans++;
	b[x][y]=1;
	int s=0;
	for(int i=1;i<=4;i++)
	{
		int xx=x+xn[i];
		int yy=y+yn[i];
		if(xx>0&&yy>0&&xx<=n&&yy<=n&&a[xx][yy])
		{
			if(!b[xx][yy])
				dfs(xx,yy);
			s++;
		}
	}
	anss=anss+4-s;
	c[x][y]=4-s;
}
int main()
{
	freopen("perimeter.in","r",stdin);
	freopen("perimeter.out","w",stdout);
	cin>>n;
	hh=1;
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
		{
			char h;
			cin>>h;
			if(h=='.')
			{
				a[i][j]=0;
				hh=0;
			}
			else
				a[i][j]=1;
		}
	if(hh==1)
	{
		cout<<n*n<<" "<<4*n<<endl;
		return 0;
	}
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
			if(!b[i][j]&&a[i][j])
			{
				ans=0;
				anss=0;
				dfs(i,j);
				if(ans>maxn)
				{
					maxn=ans;
					maxnn=anss;
				}
				if(ans==maxn&&anss<maxnn)
					maxnn=anss;
			}
	cout<<maxn<<" "<<maxnn<<endl;
}

T3

题目描述

从农场里奶牛Bessie的牧草地向远端眺望，可以看到巍峨壮丽的山脉绵延在地平线上。山脉里由N座山峰（1≤N≤10^5）。如果我们把Bessie的视野想象成xy平面，那么每座山峰都是一个底边在x轴上的三角形。山峰的两腰均与底边成45度角，所以山峰的峰顶是一个直角。于是山峰i可以由它的峰顶坐标(xi,yi)精确描述。没有两座山峰有完全相同的峰顶坐标。
Bessie尝试数清所有的山峰，然而由于它们几乎是相同的颜色，所以如果一座山峰的峰顶在另一座山峰的三角形区域的边界上或是内部，她就无法看清。
请求出Bessie能够看见的不同的山峰的峰顶的数量，也就是山峰的数量。

输入

输入的第一行包含N。以下N行每行包含xi（0≤xi≤10^{9）和yi（1≤yi≤10}9），描述一座山峰的峰顶的坐标。

输出

输出Bessie能够分辨出的山峰的数量。

样例输入

样例输出

提示

在这个例子中，Bessie能够看见第一座和最后一座山峰。第二座山峰被第一座山峰掩盖了。

解题思路

又是一道玄学的题目呢~，我们先找出它底边的左端点和右端点，排序后就进行一些玄学的操作，最后输出值就ok

#include<iostream>
#include<cstdio>
#include<algorithm> 
using namespace std;
long long n,ans,maxn;
struct abc{
	int l,r;
}m[100010];
bool cmp(abc a,abc b)
{
	return a.l<b.l||a.l==b.l&&a.r>b.r;
}
int main()
{
	freopen("mountains.in","r",stdin);
	freopen("mountains.out","w",stdout);
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		long long x,y;
		scanf("%d%d",&x,&y);
		m[i].l=x-y;
		m[i].r=x+y;
	}
	sort(m+1,m+n+1,cmp);
	for(int i=1;i<=n;i++)
		if(m[i].r>maxn)
		{
			ans++;
			maxn=m[i].r;
		}
	cout<<ans<<endl;
}