幻想迷宫【DFS】

题目大意：

给出一个迷宫，走到这个迷宫边界时可以瞬移。求从$S$点开始，能否走到无限远。
$Input$

5 4
##.#
##S#
#..#
#.##
#..#
5 4
##.#
##S#
#..#
..#.
#.##

$Output$

Yes
No

---

思路：

哇。。。这是我做过的最难得$DFS$题目。。。
从5月开始做，陆陆续续地，今天终于做完了。。。
啊啊啊啊啊累死我了（今天攻了一整天这道题，终于过了。。。）
不愧是蓝题。
共耗时：72天8时

---

这道题要我们求能否走到无限远处，其实很容易想到，它就是要我们求能否从起点到达另一个起点！（因为会瞬移）
图片转自https://www.luogu.org/blog/GNAQ/solution-p1363

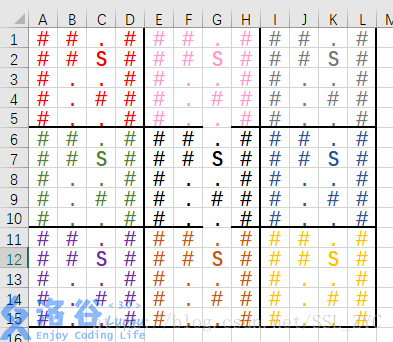
如果能从粉色的$S$走到黑色的$S$,那么就肯定能从黑色的$S$走到棕色的$S$，那么也能走到下一个$S$。。。就能走到无限远处。
那么第一种思路肯定是开一个$9\times9$的矩阵（如上图），一般来说，$9\times9$就足够我们存所有答案了。
但是如果遇到下面这组数据：

6 20
#.##.##.##.##.##.##.
#.##.##.##.##.##.##.
#.##.##.##.##.##.##.
S.#..#..#..#..#..#..
##..#..#..#..#..#..#
#..#..#..#..#..#..##

那就gg了。
那么我们又不可能开更大了，所以就只能有一种方法：
重复使用一个矩阵。
那么就真正得顺瞬移了。每当走出界时，就将它瞬移到对面的那个格子。
那么就有很多细节了。打代码时一定要注意细节。

---

代码：

#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;

const int dx[]={0,0,0,1,-1};
const int dy[]={0,1,-1,0,0};
int n,m,sx,sy;
int a[1511][1511],b[3011][3011],c[1511][1511];
char ch;

int dfs(int x,int y)  //深搜
{
    if (x<0) return(dfs(n*2-1,y)); 
    if (y<0) return(dfs(x,m*2-1)); 
    if (x>=n*2) return(dfs(0,y)); 
    if (y>=m*2) return(dfs(x,0));  //判断是否瞬移 
    if (b[x][y]||a[x%n][y%m]) return 0;  //不能访问
    if (c[x%n][y%m]) return 1;  //到达其他起点
    b[x][y]=1;
    c[x%n][y%m]=1;
    for (int i=1;i<=4;i++)
      if (dfs(x+dx[i],y+dy[i])) return 1;  //继续搜
    return 0;
}

int main()
{
    while (cin>>n>>m)  //多组数据
    {
        memset(a,0,sizeof(a));
        memset(b,0,sizeof(b));
        memset(c,0,sizeof(c));
        for (int i=0;i<n;i++)
         for (int j=0;j<m;j++)
         {
            cin>>ch;
            if (ch=='#') a[i][j]=1;
            if (ch=='S')
            {
                sx=i;
                sy=j;
            }
         }
        if (dfs(sx,sy)) printf("Yes\n");
         else printf("No\n");
    }
    return 0;
}