圣章-精灵使的魔法语【线段树】

题目大意：

给出一个由“（”和“）”组成的字符串，以及$m$种要求：

1. $Change$ $x$,将第$x$位的括号改变方向。
   • $Query$ $l$ $r$，输出若要让$l$到$r$之间的括号全部匹配，要在左边加入多少个“（”，右边加上多少个“）”。

   • $Input$

     4 3
     )()(
     Query 1 4
     Change 3
     Query 1 4

     $Output$

     1 1
     1 3
     

     ---

     思路：

     好难啊这道题。。。
     重点是只有$O(n)$或$O(nlogn)$才能过！！！
     改了我一个下午$+$晚上1小时，共耗时$6.5hour$。
     还有，这道题卡常，还得优化一下才能过。。。

     ---

     这道题要我们区间修改和查询，自然是线段树。
     一棵普通的线段树长这个样子：
     
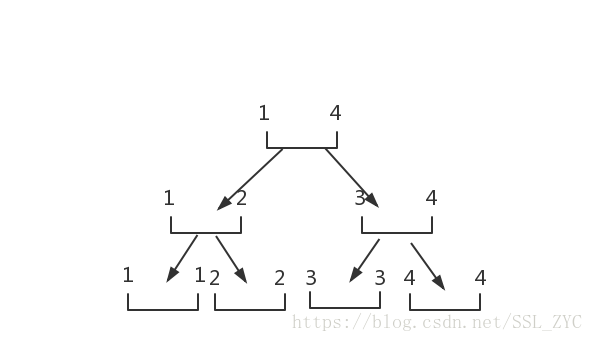
     我们把这棵线段树的叶子节点赋值为$s[i]$（即输入的括号串的每一个字符）。拿样例来说，就是这个样子：
     
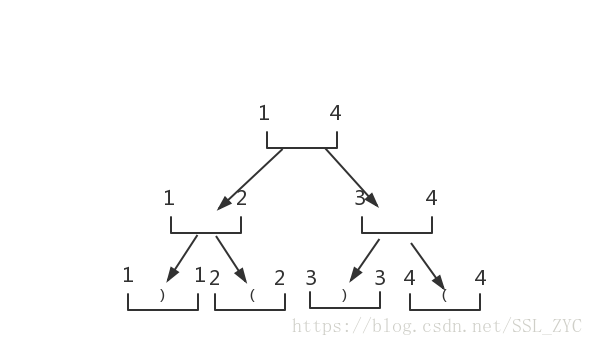
     再将这棵树合并
     
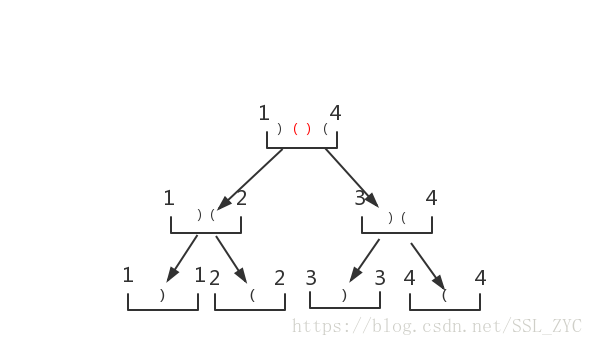
     把红色部分的可以匹配的去掉
     
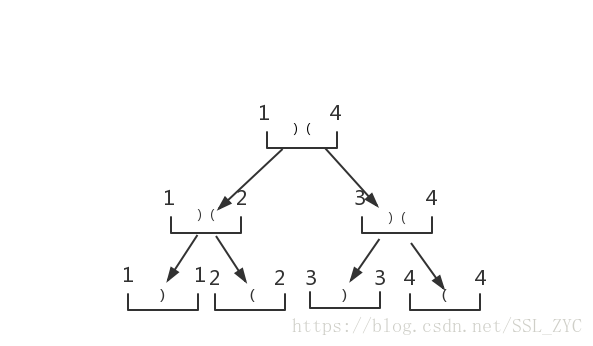
     就可以求出每个区间需要匹配多少号啦！
     那么对于$Change$操作，我们可以递归找到需要改变的点
     
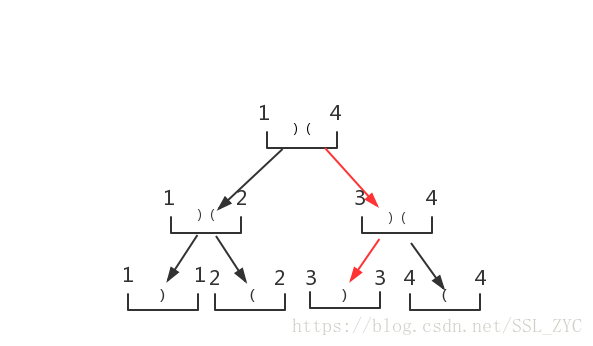
     将这个字符改变
     
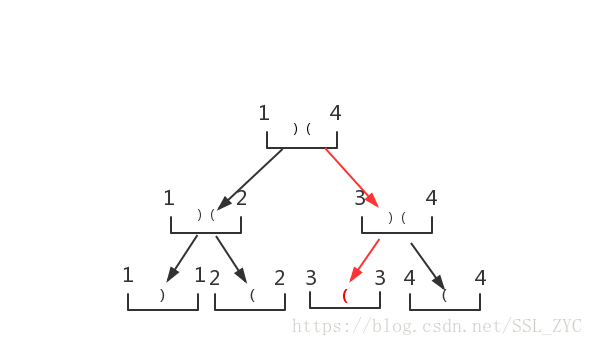
     递归回去
     
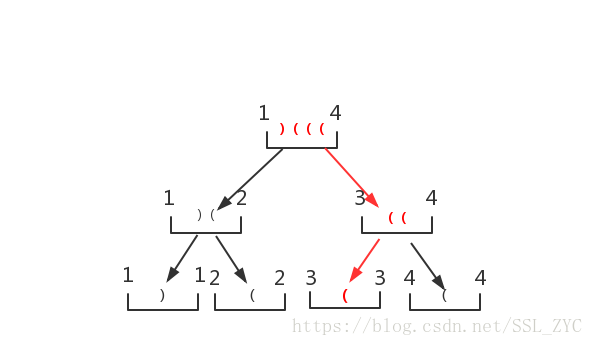
     就可以啦！
     这个过程细节十分多，思路必须特备清晰！

     ---

     代码：

     #include <cstdio>
     #include <iostream>
     #include <cstring>
     #define fre(x) freopen(#x".in","r",stdin),freopen(#x".out","w",stdout);
     using namespace std;
     
     int n,m,x,y,t,L,R;
     char c[7],s[300001];
     
     struct node
     {
         int l,r,lnum,rnum;
     }tree[800001];
     
     void make(int x)  //建树
     {
         if (tree[x].r==tree[x].l)  //叶子节点
         {
             if (s[tree[x].l-1]==')') tree[x].lnum=1;
             else tree[x].rnum=1;  //赋值字符
             return;
         }
         int mid=(tree[x].l+tree[x].r)/2;
         tree[x*2].l=tree[x].l;
         tree[x*2].r=mid;
         tree[x*2+1].l=mid+1;
         tree[x*2+1].r=tree[x].r;  //给子节点赋值
         make(x*2);
         make(x*2+1);  //继续建图
         tree[x].lnum=tree[x*2].lnum+max(0,tree[x*2+1].lnum-tree[x*2].rnum);
         tree[x].rnum=tree[x*2+1].rnum+max(0,tree[x*2].rnum-tree[x*2+1].lnum);  //求出每边必须增加几个括号
         return;
     }
     
     void find(int x,int l,int r)  //Query操作
     {
         if (l==tree[x].l&&r==tree[x].r)  //找到这部分
         {
             L=tree[x].lnum;
             R=tree[x].rnum;  //赋值
             return;
         }
         if (tree[x].l==tree[x].r) return; //叶子节点
         int mid=(tree[x].l+tree[x].r)/2;
         if (r<=mid)  //完全在左边
         {
             find(x*2,l,r);
             return;
         }
         if (l>mid)  //完全在右边
         {
             find(x*2+1,l,r);
             return;
         }
         find(x*2,l,mid);  //两边都有
         int ll=L,rr=R;
         find(x*2+1,mid+1,r);
         int lll=L,rrr=R;
         L=ll+max(0,lll-rr);
         R=rrr+max(0,rr-lll);
         return;
     }
     
     void makes(int x,int p)  //Change操作
     {
         if (tree[x].l==p&&tree[x].r==p)  //找到更改点
         {
             tree[x].lnum=1-tree[x].lnum;
             tree[x].rnum=1-tree[x].rnum;  //更改（1变0,0变1）
             return;
         }
         if (tree[x].l==tree[x].r) return;  //叶子节点
         int mid=(tree[x].l+tree[x].r)/2;
         if (p<=mid) makes(x*2,p);
          else makes(x*2+1,p);  //log(n)找出更改点
         tree[x].lnum=tree[x*2].lnum+max(0,tree[x*2+1].lnum-tree[x*2].rnum);
         tree[x].rnum=tree[x*2+1].rnum+max(0,tree[x*2].rnum-tree[x*2+1].lnum);
         return;
     }
     
     int main()
     {
         fre(elf);
         scanf("%d%d",&n,&m);
         scanf("%s",s);
         tree[1].l=1;
         tree[1].r=n;    
         make(1);  //建图
         for (int i=1;i<=m;i++)
         {
             scanf("%s",c);
             if (c[0]=='Q')
             {
                 L=R=0;
                 scanf("%d%d",&x,&y);
                 find(1,x,y);
                 printf("%d %d\n",L,R);
             }
             else
             {
                 scanf("%d",&x);
                 makes(1,x);
             }
         }
         return 0;
     }