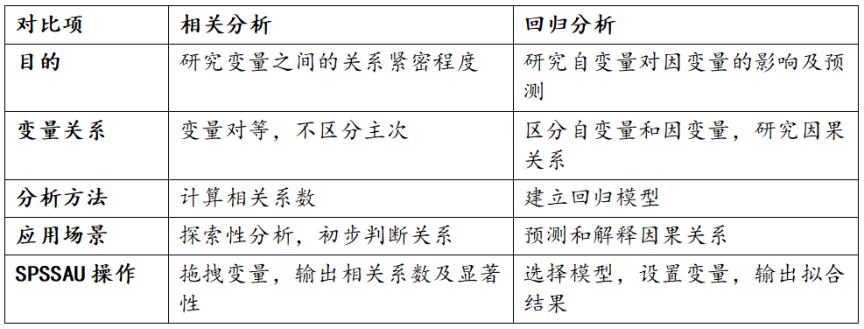
相关分析与回归分析的区别与联系

相关分析与回归分析是统计学中两种常用的数据分析方法，它们都用于研究变量之间的关系，但在目的、方法和应用场景上存在显著区别。以下是两者的详细对比：

1. 目的不同

• 相关分析：
  用于研究两个或多个变量之间是否存在关系，以及关系的紧密程度。它不区分自变量和因变量，变量之间是对等的关系。
  例如：研究“网购满意度”与“重复购买意愿”之间是否存在相关性。
• 回归分析：
  用于研究自变量（X）对因变量（Y）的影响关系，并建立数学模型进行预测。它明确区分自变量和因变量。
  例如：研究“广告投入”对“销售额”的影响。

2. 变量关系不同

• 相关分析：
  变量之间是对等的关系，不区分主次。
  例如：研究“身高”与“体重”的相关性，两者没有明确的因果关系。
• 回归分析：
  变量之间有明确的因果关系，自变量影响因变量。
  例如：研究“学习时间”对“考试成绩”的影响，学习时间是自变量，考试成绩是因变量。

3. 分析方法不同

• 相关分析：
  通过计算相关系数（如Pearson、Spearman、Kendall）来衡量变量之间的关系强度和方向。
  • 相关系数大于0表示正相关，小于0表示负相关。
  • 相关系数绝对值越大，关系越紧密。
• 回归分析：
  通过建立回归模型（如线性回归、Logistic回归）来量化自变量对因变量的影响，并预测因变量的值。
  • 例如：线性回归模型Y = aX + b，其中a表示自变量X对因变量Y的影响程度。

4. 应用场景不同

• 相关分析：
  适用于探索性分析，初步判断变量之间是否存在关系。
  例如：在回归分析之前，先通过相关分析筛选出与因变量相关的自变量。
• 回归分析：
  适用于预测和解释变量之间的因果关系。
  例如：预测“房价”基于“面积”、“地段”等自变量的影响。

5. 联系

• 相关分析是回归分析的前提条件。只有变量之间存在相关关系，才可能进一步进行回归分析。
• 从广义上讲，回归分析是从属于相关分析的，但回归分析更侧重于因果关系和预测。

6. SPSSAU中的操作

• 相关分析：
  在SPSSAU(在线SPSS)中，【通用方法】模块选择“相关”，用户可以直接拖拽变量进行相关分析，系统会自动输出相关系数及显著性结果。
  例如：分析“网购满意度”与“重复购买意愿”的相关性。
• 回归分析：
  在SPSSAU(网页SPSS)中，用户可以选择回归模型（如线性回归、Logistic回归），并设置自变量和因变量，系统会输出模型拟合结果及预测值。
  例如：分析“广告投入”对“销售额”的影响。

总结

通过以上对比，可以清晰地理解相关分析与回归分析的区别及其适用场景。在实际数据分析中，通常先进行相关分析，再根据需要进行回归分析。