图形学各种二维基础变换，原来线性代数还能这么用，太牛了

缩放变换

均匀缩放

• 若想将一个图形缩小0.5倍

  

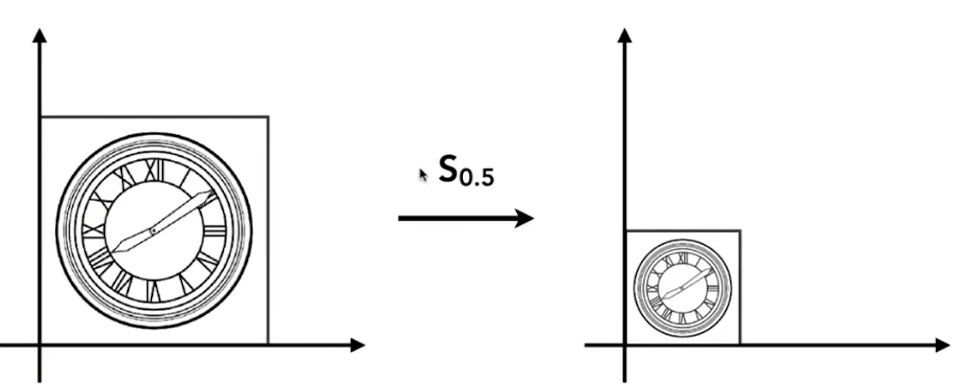
• 若x乘上缩放值s等于x撇，y同理，则$\begin{array}{rl}& x^{\prime }=sx\\ & y^{\prime }=sy\end{array}$，这样就表示了x缩小了s倍，y也是

• 将其转为矩阵操作则是在前面乘上一个缩放矩阵$\left[\begin{array}{l}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{ll}s& 0\\ 0& s\end{array}\right]\left[\begin{array}{l}x\\ y\end{array}\right]$，根据矩阵乘法性质，其中的x撇和y撇最后乘出来就是上述的sx和sy。

• 变换矩阵为$\left[\begin{array}{ll}s& 0\\ 0& s\end{array}\right]$

非均匀缩放

• x缩放0.5倍，y不变

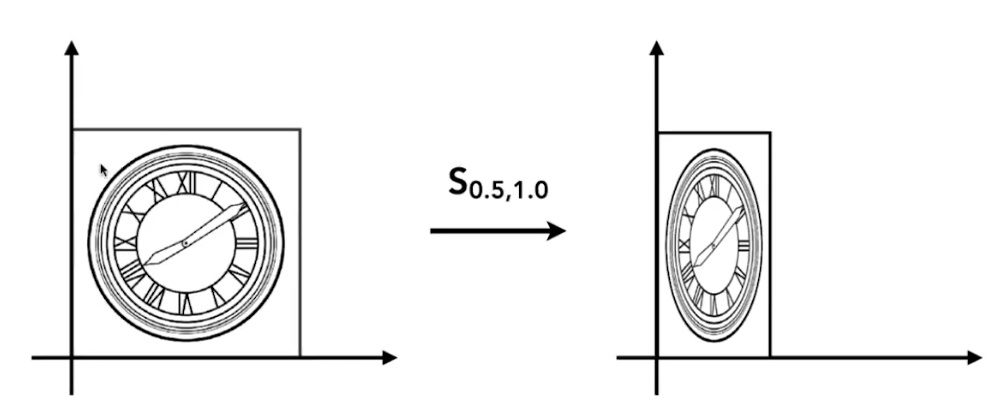
• 和上述公式一样，只不过将对角矩阵的下面那个换一下就行 $\left[\begin{array}{l}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{cc}{s}_x& 0\\ 0& s_y\end{array}\right]\left[\begin{array}{l}x\\ y\end{array}\right]$
• 其中sx为x轴的缩放倍数，sy为y轴。
• 变换矩阵为$\left[\begin{array}{cc}{s}_x& 0\\ 0& s_y\end{array}\right]$

镜像变换

• 若要将x沿x轴镜像，则表达为$\begin{array}{rl}& x^{\prime }=-x\\ & y^{\prime }=y\end{array}$

• 其矩阵形式则为$\left[\begin{array}{l}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{cc}-1& 0\\ 0& 1\end{array}\right]\left[\begin{array}{l}x\\ y\end{array}\right]$
• 变换矩阵为$\left[\begin{array}{cc}-1& 0\\ 0& 1\end{array}\right]$

剪切变换

• x轴拉长，y轴不变

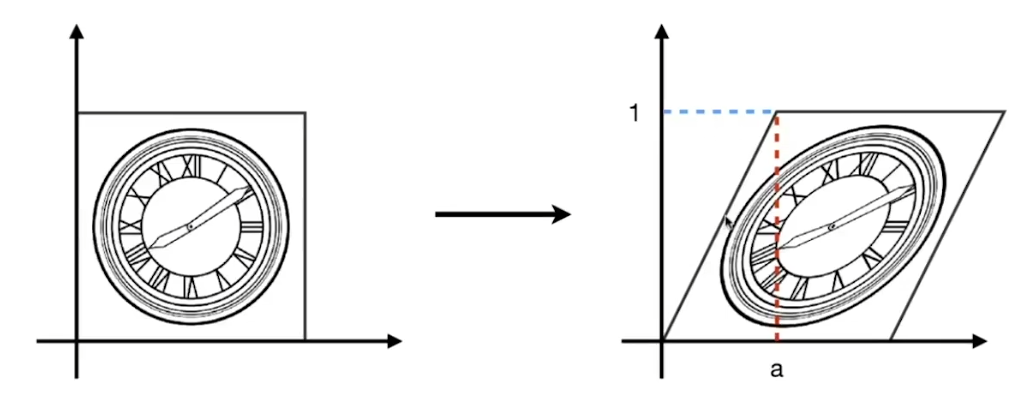
• 当y=0时，水平方向不变
• 当y=1时，水平方向向右移动a个位置
• 于是可推出，当y为1/2时，则移动后的x应该在原本的x+ay处，也就是x根据变换后为x+ay，y不变
• 用矩阵表达则为$\left[\begin{array}{l}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{ll}1& a\\ 0& 1\end{array}\right]\left[\begin{array}{l}x\\ y\end{array}\right]$
• 变换矩阵为$[\begin{array}{ll}& \\ 1& a\\ 0& \end{array}$