基于用户的协同过滤算法的电影推荐（稀疏矩阵）含代码和Netflix数据

推荐问题是大数据的典型应用，利用已知的用户浏览历史和评分等行为，猜测用户兴趣，进行个性化的推荐

数据集

用户对电影的打分（1-5），共有10000个用户和10000部电影。

• 用户id列表 users
  10000行，1列，表示用户的id
• 电影名称列表 movie_titles
  17770行，3列，格式为电影id，年份，名称
  
• 评分数据 netflix_data
  861万行，每行为一次打分，包括用户id 电影id 分数 打分日期，各项之间用空格分开，其中用户id均出现在users.txt中，电影id为1-10000的整数
  

取评分数据的80%为训练集netflix_train（689万），剩余的20%为测试集netflix_test（172万条）。

数据处理

实验使用全量数据。
将输入文件整理成维度为用户*电影的矩阵 X，其中Xij对应用户 i 对电影 j 的打分。对于分数未知的项，采取全定为 0的处理方法。

1. 从users.txt中获得userID和i的关系：

data_user = importdata('users.txt');
user_map = containers.Map({0},{0});
for i = 1:size(data_user)
    user_map(data_user(i))= i;
end

2. 读取netflix数据

读取netflix_train.txt文件，整理成维度为用户*电影的矩阵X_train

% 训练集
X_train=zeros(10000,10000);
[u,m,f,d] = textread('netflix_train.txt','%d %d %d %s');
for i = 1:size(u)
    X_train(user_map(u(i)),m(i)) = f(i);
end

读取netflix_test.txt文件，整理成维度为用户*电影的矩阵X_test

% 测试集
X_test = zeros(10000,10000);
[u,m,f,~] = textread('netflix_test.txt','%d %d %d %s');
for i = 1:size(u)
    X_test(user_map(u(i)),m(i)) = f(i);
end

3. 转化为稀疏矩阵，

由于本实验中 X 矩阵非常稀疏，使用稀疏矩阵运算，避免使用 for 循环。
在Matlab中使用spones()获得指示变量矩阵，用来记录哪些是用户已有打分的记录。

S=sparse(X) — 将矩阵X转化为稀疏矩阵的形式，即矩阵X中任何零元素去除，非零元素及其下标（索引）组成矩阵S。如果X本身是稀疏的，sparse(X)返回S

举例：

>> a=[1,0,2;0,0,1;0,0,6];
>> a
a =
     1     0     2
     0     0     1
     0     0     6
>> b=sparse(a)
b =
   (1,1)        1
   (1,3)        2
   (2,3)        1
   (3,3)        6

实验代码：
R = spones(S) 生成与 S 具有相同稀疏结构的矩阵 R，但 1 位于非零位置

X_test = sparse(X_test);
X_train = sparse(X_train);
% 指示变量
A_test = spones(X_test);
A_train = spones(X_train);

4. 保存一下数据

将X_train、X_test和A_train、A_test数据变量保存在X_matrix_sparse.mat文件中

save('X_matrix_sparse','X_train','X_test','A_test','A_train');
clear u m f d i data_user user_map;

协同过滤算法

协同过滤(Collaborative Filtering)是最经典的推荐算法之一，包含基于 user 的协同过滤和基于 item 的协同过滤两种策略。本次，实现基于用户的协同过滤算法。算法的思路非常简单，当我们需要判断用 户 i 是否喜欢电影 j，只要看与 i 相似的用户，看他们是否喜欢电影 j，并根据相似度对他们的打分进行加权平均。 用公式表达，就是:

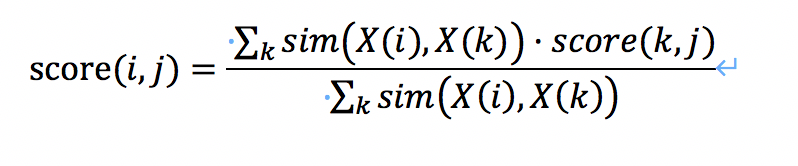
其中，X(i)表示用户 i 对所有电影的打分，对应到我们的问题中，就是 X 矩阵中第 i 行对应的 10000 维的向 量( 未 知 记 为 0 )。
𝑠𝑖𝑚(𝑋(𝑖), 𝑋(𝑘))表示用户 i 和用户 k，对于电影打分的相似度，可以采用两个向量的 cos 相似度来表示， 即:

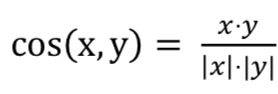
通过上面的公式，就可以对测试集中的每一条记录，计算用户可能的打分。

1. 构造相似度矩阵

关于欧式距离与余弦相似度的计算，在 MATLAB 中都有相应的函数。
夹角余弦距离Cosine distance(‘cosine’)，欧几里德距离Euclidean distance(‘euclidean’)，标准欧几里德距离Standardized Euclidean distance(‘seuclidean’)等等

使用pdist()函数得到余弦距离，1-pdist()得到两两用户间的余弦相似度cos_sim，转化为相似度矩阵X_sim，X_sim(i, j)表示用户i与用户j之间的相似度。
代码：

load('X_matrix_sparse.mat');

% 计算余弦相似度矩阵
cos_sim = 1-pdist(X_test,'cosine');

X_sim = zeros(N,N);
cursor = 1;
for i = 1:N
    X_sim(i,i) = 0;
    for j = i+1:N
        X_sim(i,j) = cos_sim(cursor);
        X_sim(j,i) = cos_sim(cursor);
        cursor = cursor + 1;
    end
end

3. 打分结果矩阵

使用协同过滤算法得到预测的打分结果。
相似度矩阵X_sim与测试集X_test相乘，再点除对X_sim进行列求和的结果。

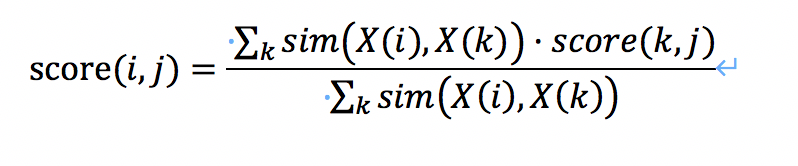
即：X_score = (X_sim*X_t)./sum(X_sim,2);

改进的加权平均
在该步骤的加权平均时，考虑到很多用户对电影的打分时未知的，所以在加群平均时，只计算对j电影有打分的用户。改后公式：

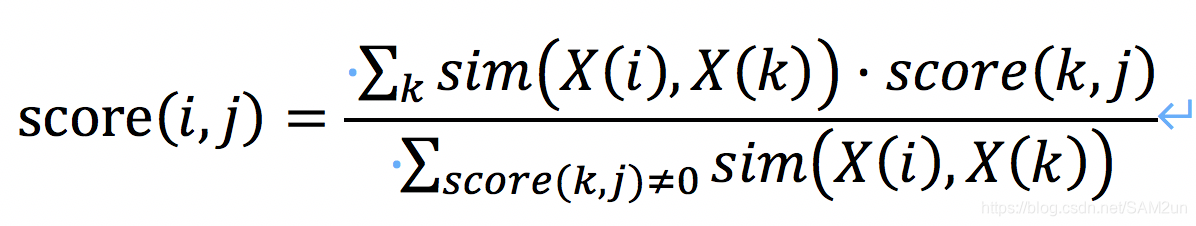
转化为矩阵计算：

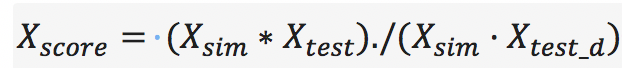
使用指标矩阵A_test作为辅助，代码实现

X_score = (X_sim*X_test)./(X_sim*A_test);
X_score = X_score.*(1-A_test) + X_test;
X_score(isnan(X_score))=0;

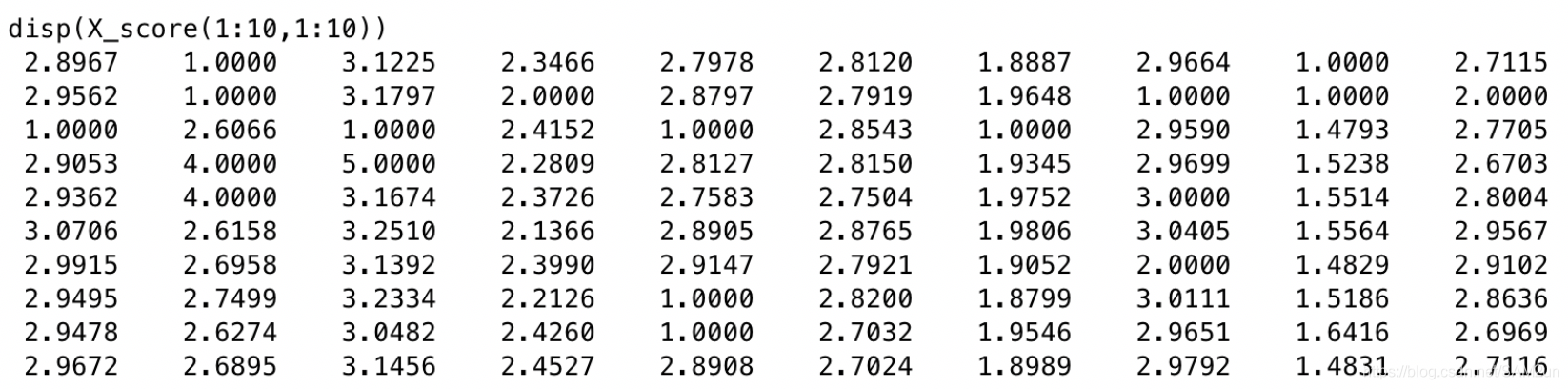
查看预测结果（前10行前10列）：

4. 计算RMSE值

采用 RMSE(Root Mean Square Error，均方根误差)作为评价指标，计算公式为：

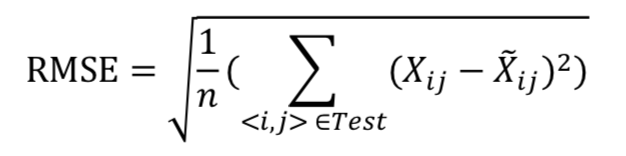
其中 Test 为所有测试样本组成的集合，𝑋𝑖𝑗为预测值，𝑋̃𝑖𝑗为实际值。
在RMSE的计算过程中，同样只关注于有评分的记录，也就是只计算在Train在有记录的评分：

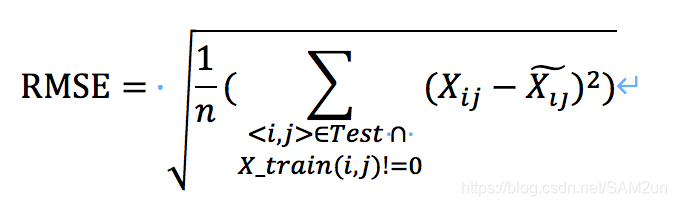
n = sum(sum(A_train==1));
RMSE = sqrt(sum(sum((X_score.*A_train-X_train).^2))/n);

输出：RMSE= 1.0225

基于梯度下降的矩阵分解算法

1. 给定 k,λ参数
   对于给定 k=50, λ = 0.01 的情况，画出迭代过程中目标函数值和测试集上 RMSE 的变化，给出最终的 RMSE，并对结果进行简单分析。
   对给定的行为矩阵 X，将其分解为 U，V 两个矩阵的乘积，使 UV 的乘积 在已知值部分逼近 X，即:Xm∗n ≈ Um∗k 𝑉𝑛∗𝑘𝑇，它们的乘积矩阵可以用来预测
   X 的未知部分。
   使用梯度下降法优化求解这个问题。目标函数是:
   

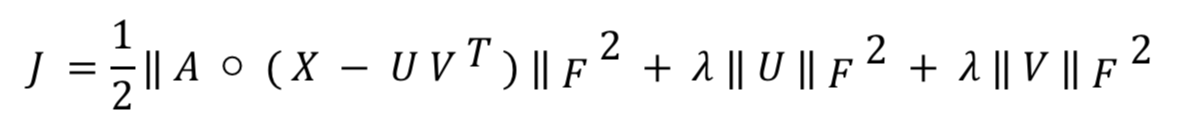
当目标函数取得最小值时，算法得到最优解。首先，我们对 U 和 V 分别求 偏导，结果如下:

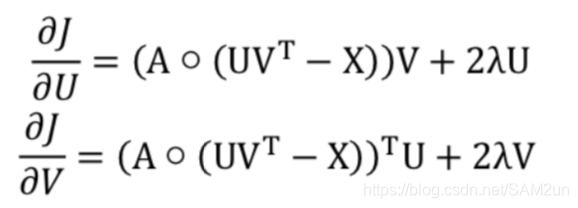
之后，我们迭代对 U 和 V 进行梯度下降，具体算法如下:

取k = 50,λ = 0.01,α = 0.0001，随机生成矩阵U和V。 代码实现如下:

i = 1;
test_len = sum(sum((A_test)~=0)); 
times = 300; % 迭代次数上限
RMSE = zeros(times,1);
 
 
J = zeros(times,1);
J(i) = 0.5*(norm(A_train.*(X_train-U*V'),'fro'))^2 + lambda*(norm(U,'fro')^2+norm(V,'fro')^2);
RMSE(i)= sqrt(sum(sum((U*V'.*A_test-X_test).^2))/test_len); 
while i < times
    tic
    i = i+1;
    j = 0.5*(norm(A_train.*(X_train-U*V'),'fro'))^2 + lambda*(norm(U,'fro')^2+norm(V,'fro')^2);
    J(i) = j;
    if j > J(i-1) break;end
    U = U - alpha*( A_train.*(U*V'-X_train)*V + 2*lambda*U );
    V = V - alpha*( (A_train.*(U*V'-X_train))'*U + 2*lambda*V );
    RMSE(i)= sqrt(sum(sum((U*V'.*A_test-X_test).^2))/test_len);
    time_toc(i)=time_toc(i-1)+toc;
end
  

保存预测结果信息:

i = i - 1;
X_score = U*V';
iterations = i-1; save('X_md.mat','k','alpha','lambda','X_score','RMSE','J','iteratio ns');

指标量:
min RMSE = 0.91865，J = 2.8920e+06 迭代次数:137 次，耗时 727.826 秒

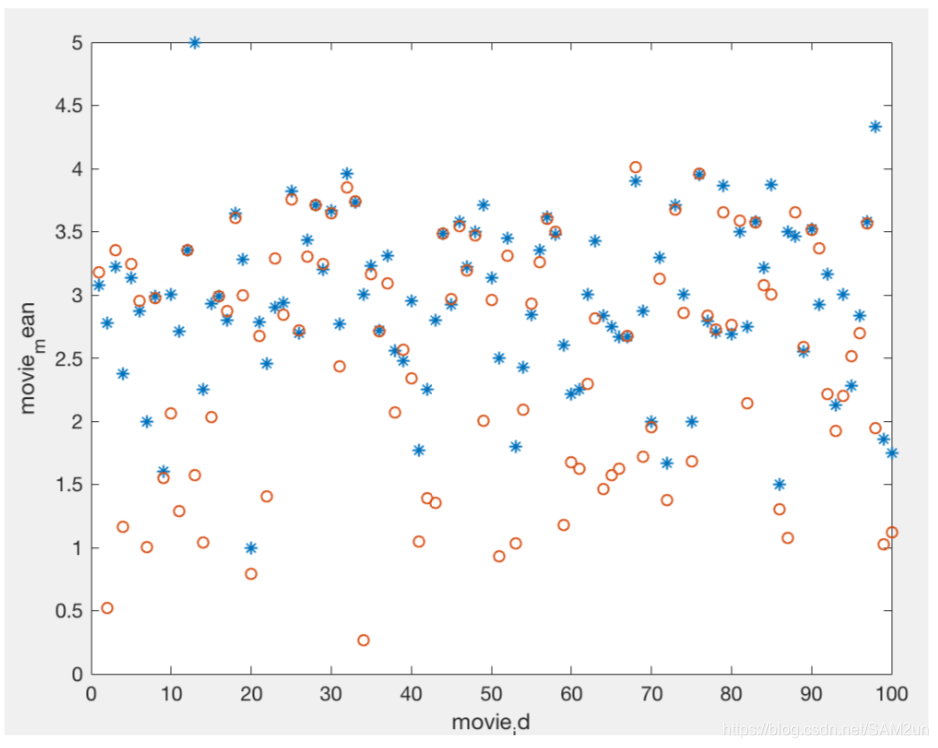
对于前 100 个电影的真实数据和预测数据的差异如图

将每次迭代的目标函数值和测试集上的 RMSE 值 plot 出来，观察算法收敛 过程中这两个指标的变化。

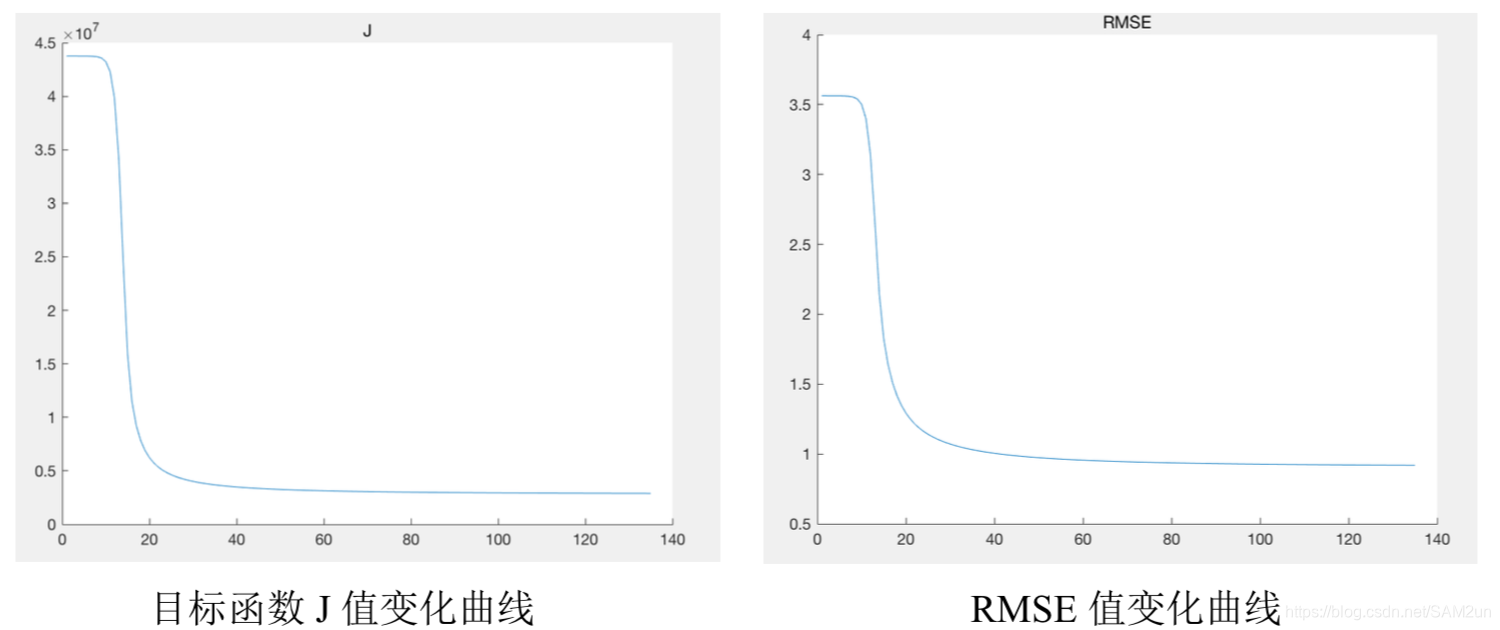
可以看出在第 1 次到第 40 次的迭代过程中，J 值和 RMSE 值都迅速下降，但是在在迭代次数大于 40 之后，J 值和 RMSE 下降都不太明显。
取不同的迭代次数作为终止条件:

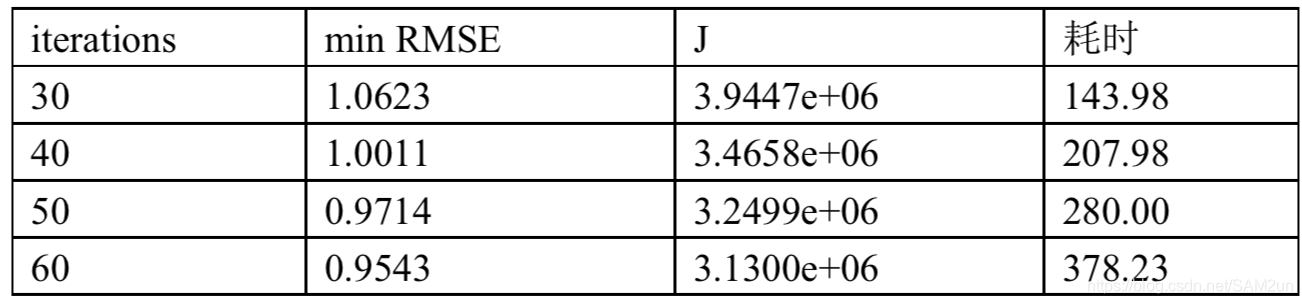
做 RMSE 和 time 随迭代次数的变化曲线:

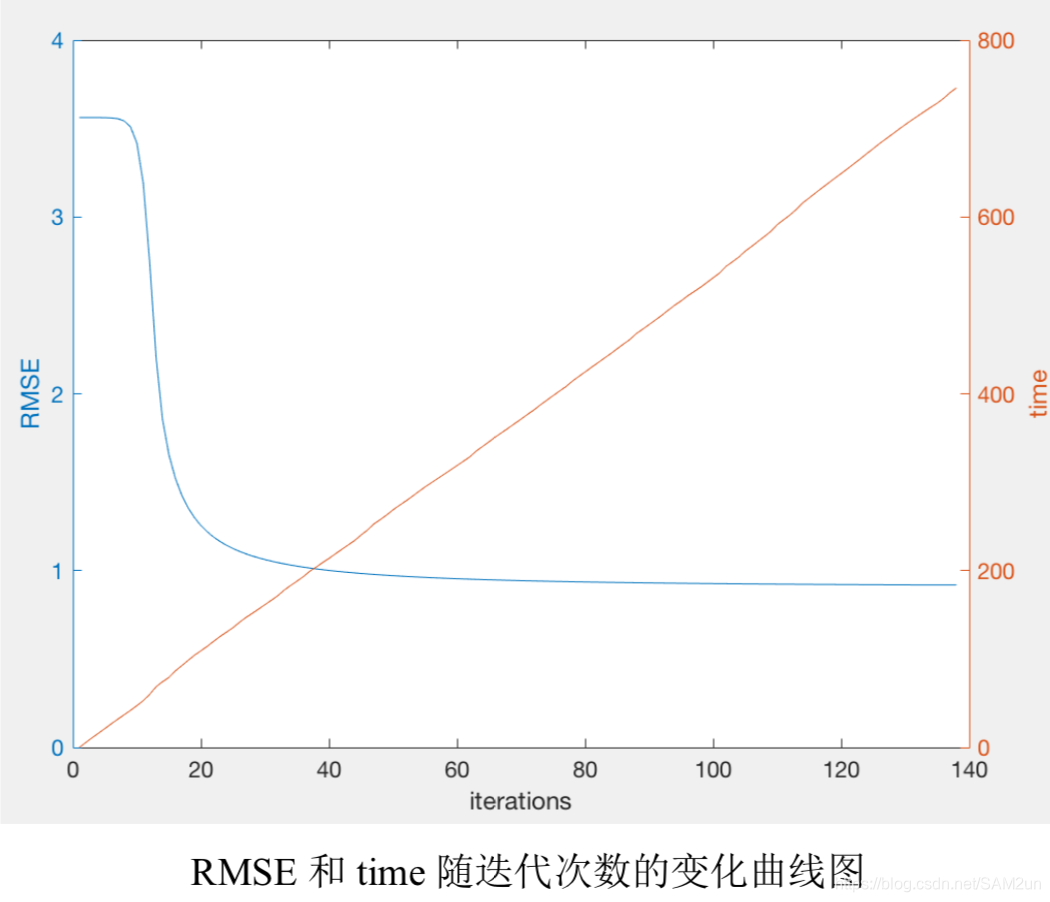
取 RMSE 和 time 曲线的交点，以 40 次迭代次数作为算法的终止条件。

(2) 调整 k,λ参数
调整 k 的值(如 20,50)和 λ 的值(如 0.001,0.1)，比较最终 RMSE 的效果，选取最优的参数组合。

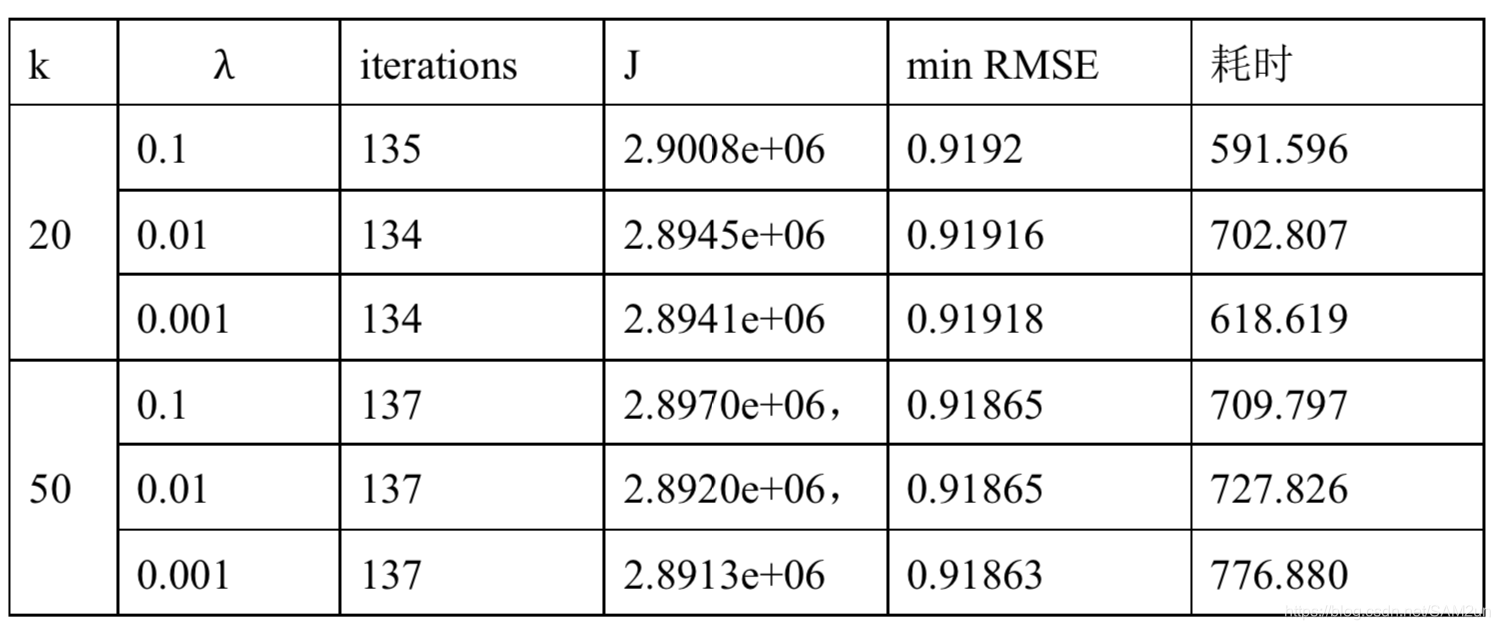
当取 40 次迭代次数作为算法的终止条件时，λ参数的取值对结果影响不显 著，参数 k 的取值对结果有一定的影响。

对比

协同过滤算法相对矩阵分解算法，RMSE 值偏大，但是时耗相对较小。当有
新的用户信息或电影信息加入时，协同过滤算法只用进行相对少量的计算就可以。
矩阵分解算法，将高维 User-Item 评分矩阵映射为两个低维用户和物品矩阵， 从而降低了矩阵的维度，且可以得到用户的喜好倾向，以及电影的特性 矩阵分 解方法，解决了数据稀疏性问题，且方便在用户特征向量和物品特征向量中添加
其它影响因素。

两算法都具有冷启动的问题，无法给新用户进行评分预测，也就无法给新用 户进行电影推荐。

数据和代码资源：
在我的资源里面可以下载运行
https://download.youkuaiyun.com/download/SAM2un/12355925