（李航统计学习方法）逻辑回归

逻辑回归是参数模型，其本质是假设数据服从伯努利分布，通过极大似然函数的方法，运用梯度上升/下降法来求解参数，从而实现数据的二分类。
逻辑回归模型在面试的过程中，最常问到的就是公式的推导过程。所以，手撕公式，很重要。

首先介绍的是逻辑斯蒂分布：

X是连续随机变量，X服从逻辑斯蒂分布。逻辑斯蒂分布的分布函数与密度函数如下：

**

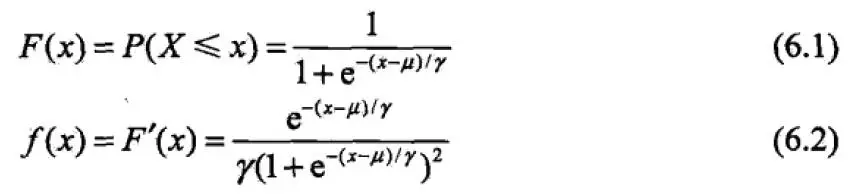
二项逻辑斯蒂回归模型

**
它是一种分类模型，由条件概率P（Y|X）表示，形式为参数化的 逻辑斯蒂分布。

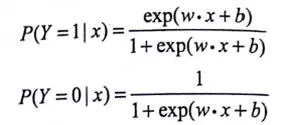
其中，exp为以e为底的指数函数，x∈Rn是输入，y∈{0,1}输出，w，b是模型参数——w是权值向量，b称作偏置，w·x是向量内积。
有了后验概率，逻辑斯蒂回归模型选择二分类中较大的那一个完成分类。
另外，逻辑斯特回归模型还有一个方便的形式，如果将权值向量w和输入向量x拓充为w=(w(1),w(2),…w(n),b)T,x=(x(1),…x(n),1)T，此时逻辑斯谛模型可以表示为：

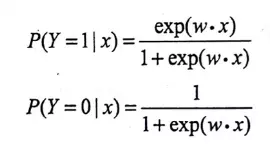
一个事件发生的几率是指该事件发生的概率与该事件不发生的概率的比值。

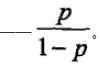
对上式进行一个对数变换后，发现：